先决条件:ML |线性回归
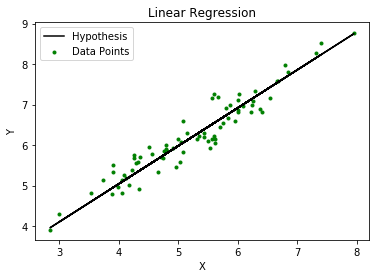
线性回归是一种监督型学习算法, 用于计算输入(X)和输出(Y)之间的线性关系。
普通线性回归涉及的步骤是:
培训阶段:计算以最小化成本。预测输出:对于给定的查询点,
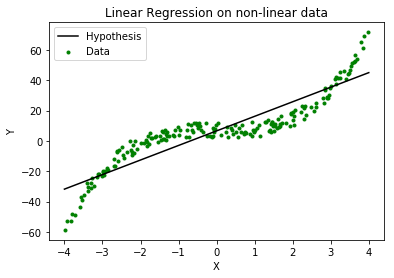
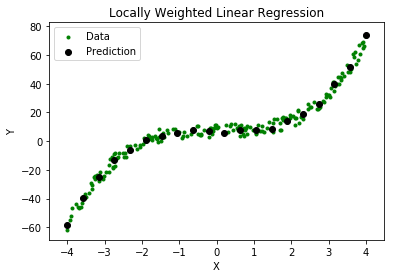
从下图可以明显看出, 当X和Y之间存在非线性关系时, 该算法不能用于进行预测。在这种情况下, 将使用局部加权线性回归。
局部加权线性回归:
局部加权线性回归是一种非参数算法, 也就是说, 该模型不像常规线性回归那样学习固定的参数集。相当的参数
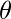
为每个查询点分别计算
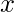
。在计算时
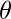
, 对训练集中位于
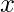
比远离的点
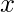
.
修改后的成本函数为:
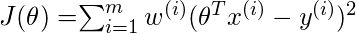
其中
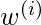
是与训练点相关的非负"权重"
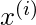
.
对于
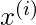
位于更靠近查询点的位置
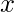
, 的价值
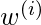
很大, 而
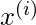
躺在远离
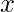
价值
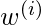
是小。
典型的选择

是:
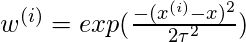
其中
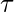
称为带宽参数, 并控制
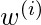
随距离而下降
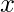
显然, 如果
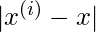
是小
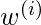
接近1, 如果
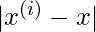
大
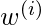
接近0。
因此, 训练集点更靠近查询点
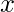
贡献更多的成本
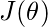
比远离的点
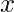
.
例如 -
考虑一个查询点
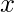
= 5.0并让
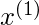
和
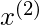
是训练集中的两点
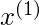
= 4.9并且
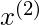
= 3.0。
使用公式
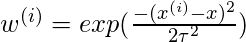
与
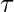
= 0.5:
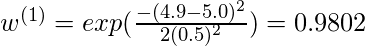
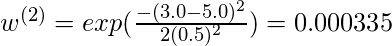
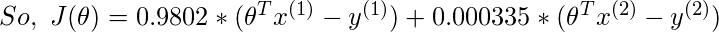
因此, 权重随着指数之间的距离呈指数下降
和
增加, 因此预测的误差贡献也增加了
成本。
因此, 在计算时
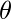
, 我们更注重减少
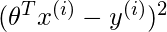
对于更靠近查询点的点(具有更大的
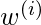
)。
局部加权线性回归涉及的步骤为:
计算以最小化成本。预测输出:对于给定的查询点,
要记住的要点:
- 局部加权线性回归是一种监督学习算法。
- 它是一种非参数算法。
- 没有训练阶段。所有工作都在测试阶段/进行预测时完成。

