ML算法： K-means++算法详细指南

先决条件： K均值聚类–简介

标准K均值算法的缺点：

K-means算法的一个缺点是它对质心或均值的初始化很敏感。因此, 如果将质心初始化为"远距离"点, 则它可能最终没有与之关联的点, 并且同时, 可能有多个群集最终与单个质心链接。同样, 一个以上的质心可能会初始化到同一群集中, 从而导致较差的群集。例如, 考虑下面显示的图像。

质心的初始化不佳会导致聚类不佳。

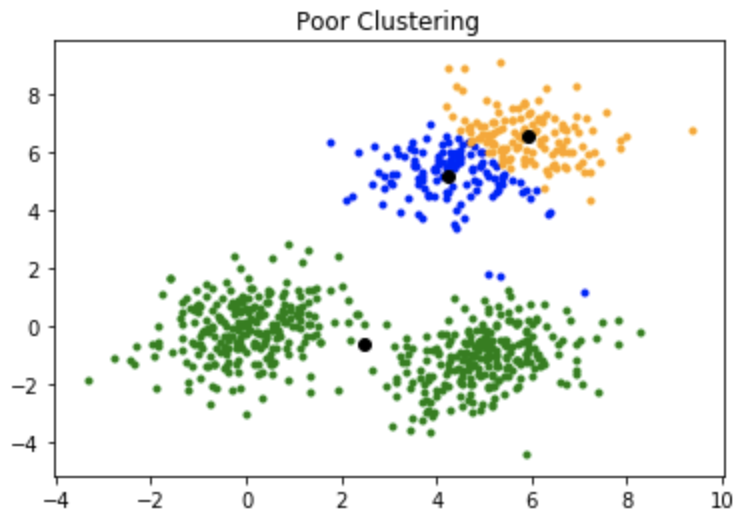
这就是集群的样子：

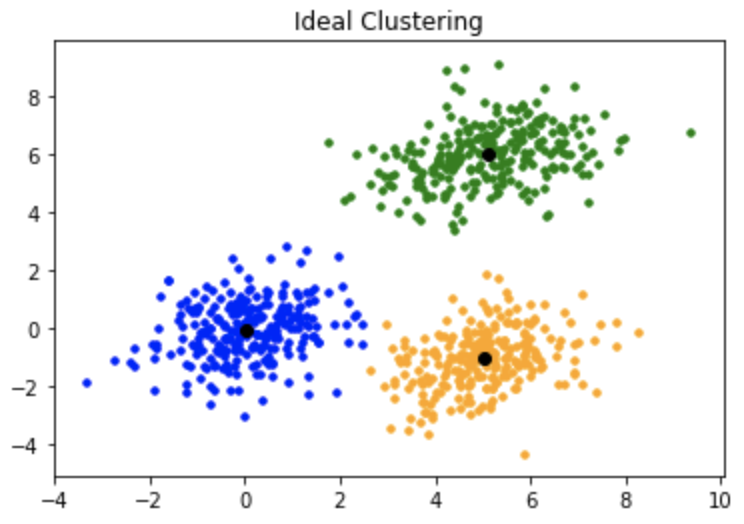
K均值++：

为了克服上述缺点, 我们使用K-means++。该算法可确保对质心进行更智能的初始化, 并提高聚类的质量。除初始化外, 其余算法与标准K均值算法相同。也就是说, K-means++是标准的K-means算法, 并结合了更智能的质心初始化。

初始化算法：

涉及的步骤是：

从数据点中随机选择第一个质心。对于每个数据点, 计算其与最近的, 先前选择的质心的距离。从数据点中选择下一个质心, 以使选择一个点作为质心的概率与其到最近的先前选择的质心的距离成正比。 (即, 最有可能选择距最近的质心最大距离的点作为质心)重复步骤2和3, 直到对k个质心进行了采样

直觉：

通过遵循上述初始化过程, 我们选择了彼此远离的质心。这增加了最初拾取位于不同簇中的质心的机会。而且, 由于质心是从数据点拾取的, 因此每个质心最后都有一些与之关联的数据点。

实现

考虑具有以下分布的数据集：

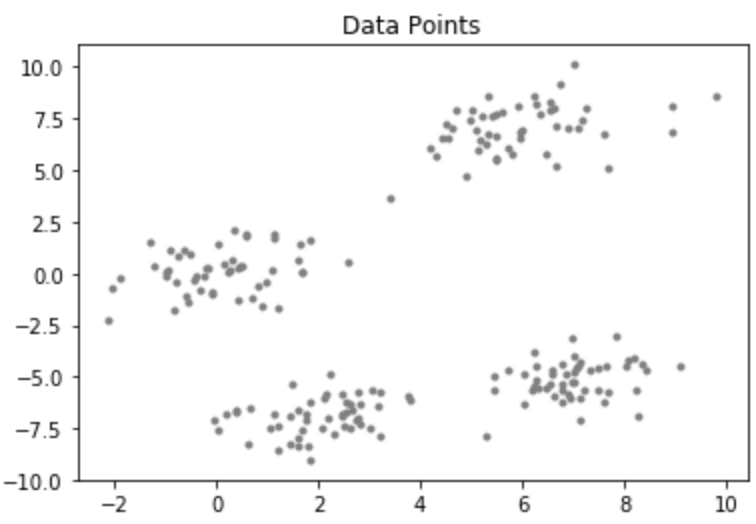
代码：KMean ++算法的Python代码

# importing dependencies
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import sys
   
# creating data
mean_01 = np.array([ 0.0 , 0.0 ])
cov_01 = np.array([[ 1 , 0.3 ], [ 0.3 , 1 ]])
dist_01 = np.random.multivariate_normal(mean_01, cov_01, 100 )
   
mean_02 = np.array([ 6.0 , 7.0 ])
cov_02 = np.array([[ 1.5 , 0.3 ], [ 0.3 , 1 ]])
dist_02 = np.random.multivariate_normal(mean_02, cov_02, 100 )
   
mean_03 = np.array([ 7.0 , - 5.0 ])
cov_03 = np.array([[ 1.2 , 0.5 ], [ 0.5 , 1 , 3 ]])
dist_03 = np.random.multivariate_normal(mean_03, cov_01, 100 )
   
mean_04 = np.array([ 2.0 , - 7.0 ])
cov_04 = np.array([[ 1.2 , 0.5 ], [ 0.5 , 1 , 3 ]])
dist_04 = np.random.multivariate_normal(mean_04, cov_01, 100 )
   
data = np.vstack((dist_01, dist_02, dist_03, dist_04))
np.random.shuffle(data)
   
# function to plot the selected centroids
def plot(data, centroids):
     plt.scatter(data[:, 0 ], data[:, 1 ], marker = '.' , color = 'gray' , label = 'data points' )
     plt.scatter(centroids[: - 1 , 0 ], centroids[: - 1 , 1 ], color = 'black' , label = 'previously selected centroids' )
     plt.scatter(centroids[ - 1 , 0 ], centroids[ - 1 , 1 ], color = 'red' , label = 'next centroid' )
     plt.title( 'Select % d th centroid' % (centroids.shape[ 0 ]))
      
     plt.legend()
     plt.xlim( - 5 , 12 )
     plt.ylim( - 10 , 15 )
     plt.show()
           
# function to compute euclidean distance
def distance(p1, p2):
     return np. sum ((p1 - p2) * * 2 )
   
# initialization algorithm
def initialize(data, k):
     '''
     initialized the centroids for K-means++
     inputs:
         data - numpy array of data points having shape (200, 2)
         k - number of clusters 
     '''
     ## initialize the centroids list and add
     ## a randomly selected data point to the list
     centroids = []
     centroids.append(data[np.random.randint(
             data.shape[ 0 ]), :])
     plot(data, np.array(centroids))
   
     ## compute remaining k - 1 centroids
     for c_id in range (k - 1 ):
          
         ## initialize a list to store distances of data
         ## points from nearest centroid
         dist = []
         for i in range (data.shape[ 0 ]):
             point = data[i, :]
             d = sys.maxsize
              
             ## compute distance of 'point' from each of the previously
             ## selected centroid and store the minimum distance
             for j in range ( len (centroids)):
                 temp_dist = distance(point, centroids[j])
                 d = min (d, temp_dist)
             dist.append(d)
              
         ## select data point with maximum distance as our next centroid
         dist = np.array(dist)
         next_centroid = data[np.argmax(dist), :]
         centroids.append(next_centroid)
         dist = []
         plot(data, np.array(centroids))
     return centroids
   
# call the initialize function to get the centroids
centroids = initialize(data, k = 4 )

输出如下：

注意：尽管K-means++中的初始化在计算上比标准K-means算法昂贵, 但对于K-means++, 收敛到最佳状态的运行时间大大减少了。这是因为最初选择的质心可能已经位于不同的簇中。

---