线性回归:
它是预测分析的基本类型和常用类型。这是一种统计方法, 用于对因变量和给定的一组自变量之间的关系进行建模。
有两种类型:
- 简单线性回归
- 多元线性回归
让我们讨论使用Python进行多元线性回归。
多个线性回归尝试通过将线性方程序拟合到观测数据来对两个或多个特征与响应之间的关系进行建模。执行多重线性回归的步骤几乎与简单线性回归的步骤相似。差异在于评估。我们可以使用它来找出哪个因素对预测的输出影响最大, 现在不同的变量相互关联。
在这里:Y = b0 + b1 * x1 + b2 * x2 + b3 * x3 +……bn * xn Y =因变量, x1, x2, x3, ……xn =多个自变量
回归模型的假设:
- 线性度:因变量和自变量之间的关系应该是线性的。
- 同方性:误差应保持恒定。
- 多元正态性:多元回归假设残差是正态分布的。
- 缺乏多重共线性:假定数据中很少或没有多重共线性。
虚拟变量 -
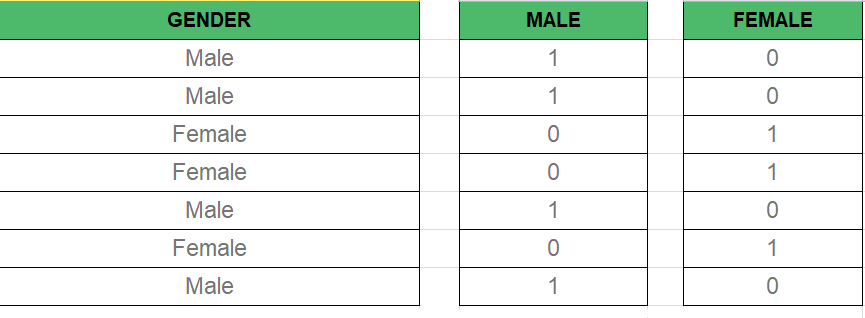
如我们所知, 在多元回归模型中, 我们使用了大量分类数据。使用分类数据是一种将非数字数据包括到各自的回归模型中的好方法。分类数据是指表示类别的数据值, 该数据值具有固定数量和无序数量的值, 例如, gender(male/female)。在回归模型中, 这些值可以由虚拟变量表示。
这些变量由诸如0或1之类的值组成, 代表存在和不存在分类值。
虚拟变量陷阱–
虚拟变量陷阱是两个或多个高度相关的情况。简单来说, 我们可以说一个变量可以从另一个变量的预测中进行预测。虚拟变量陷阱的解决方案是删除一个类别变量。所以如果有
米
虚拟变量然后
m-1
在模型中使用变量。
D2 = D1-1
Here D2, D1 = Dummy Variables建立模型的方法:
- 全能
- 向后淘汰
- 前向选择
- 双向消除
- 分数比较
向后消除:
第1步 :
选择一个重要级别以开始模型。
第2步 :
用所有可能的预测变量拟合整个模型。
步骤#3:
考虑具有最高P值的预测变量。如果P> SL转到步骤4, 否则模型为就绪。
步骤4 :
删除预测变量。
步骤#5:
没有此变量的模型拟合。
正向选择:
第1步 :
选择一个显着性水平以输入模型(例如SL = 0.05)
第2步 :
拟合所有简单回归模型y〜x(n)。选择P值最低的那个。
步骤#3:
保留此变量, 并在所有已有的模型上添加一个额外的预测变量, 以适合所有可能的模型。
步骤4 :
考虑具有最低P值的预测变量。如果P <SL, 请转到步骤#3, 否则模型为就绪。
任何多元线性回归模型涉及的步骤
第1步:数据预处理
- 导入库。
- 导入数据集。
- 编码分类数据。
- 避免虚拟变量陷阱。
- 将数据集分为训练集和测试集。
第2步:
将多元线性回归拟合到训练集
步骤3:
预测测试集结果。
代码1:
import numpy as np
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
def generate_dataset(n):
x = []
y = []
random_x1 = np.random.rand()
random_x2 = np.random.rand()
for i in range (n):
x1 = i
x2 = i /2 + np.random.rand() * n
x.append([ 1 , x1, x2])
y.append(random_x1 * x1 + random_x2 * x2 + 1 )
return np.array(x), np.array(y)
x, y = generate_dataset( 200 )
mpl.rcParams[ 'legend.fontsize' ] = 12
fig = plt.figure()
ax = fig.gca(projection = '3d' )
ax.scatter(x[:, 1 ], x[:, 2 ], y, label = 'y' , s = 5 )
ax.legend()
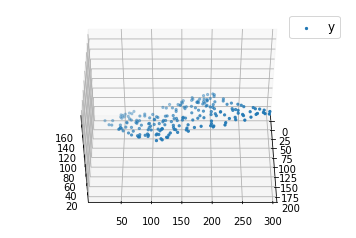
ax.view_init( 45 , 0 )
plt.show()输出如下:
代码2:
def mse(coef, x, y):
return np.mean((np.dot(x, coef) - y) * * 2 ) /2
def gradients(coef, x, y):
return np.mean(x.transpose() * (np.dot(x, coef) - y), axis = 1 )
def multilinear_regression(coef, x, y, lr, b1 = 0.9 , b2 = 0.999 , epsilon = 1e - 8 ):
prev_error = 0
m_coef = np.zeros(coef.shape)
v_coef = np.zeros(coef.shape)
moment_m_coef = np.zeros(coef.shape)
moment_v_coef = np.zeros(coef.shape)
t = 0
while True :
error = mse(coef, x, y)
if abs (error - prev_error) <= epsilon:
break
prev_error = error
grad = gradients(coef, x, y)
t + = 1
m_coef = b1 * m_coef + ( 1 - b1) * grad
v_coef = b2 * v_coef + ( 1 - b2) * grad * * 2
moment_m_coef = m_coef /( 1 - b1 * * t)
moment_v_coef = v_coef /( 1 - b2 * * t)
delta = ((lr /moment_v_coef * * 0.5 + 1e - 8 ) *
(b1 * moment_m_coef + ( 1 - b1) * grad /( 1 - b1 * * t)))
coef = np.subtract(coef, delta)
return coef
coef = np.array([ 0 , 0 , 0 ])
c = multilinear_regression(coef, x, y, 1e - 1 )
fig = plt.figure()
ax = fig.gca(projection = '3d' )
ax.scatter(x[:, 1 ], x[:, 2 ], y, label = 'y' , s = 5 , color = "dodgerblue" )
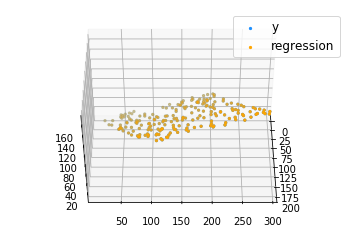
ax.scatter(x[:, 1 ], x[:, 2 ], c[ 0 ] + c[ 1 ] * x[:, 1 ] + c[ 2 ] * x[:, 2 ], label = 'regression' , s = 5 , color = "orange" )
ax.view_init( 45 , 0 )
ax.legend()
plt.show()输出如下: