本文概述
我们已经讨论了奈特的《迷宫之旅》中的《骑士之旅》和《老鼠》套装1和套装2分别。让我们讨论N Queen作为可以使用回溯解决的另一个示例问题。
N Queen是在N×N棋盘上放置N个国际象棋皇后的问题, 这样就不会有两个女王互相攻击。例如, 以下是4 Queen问题的解决方案。
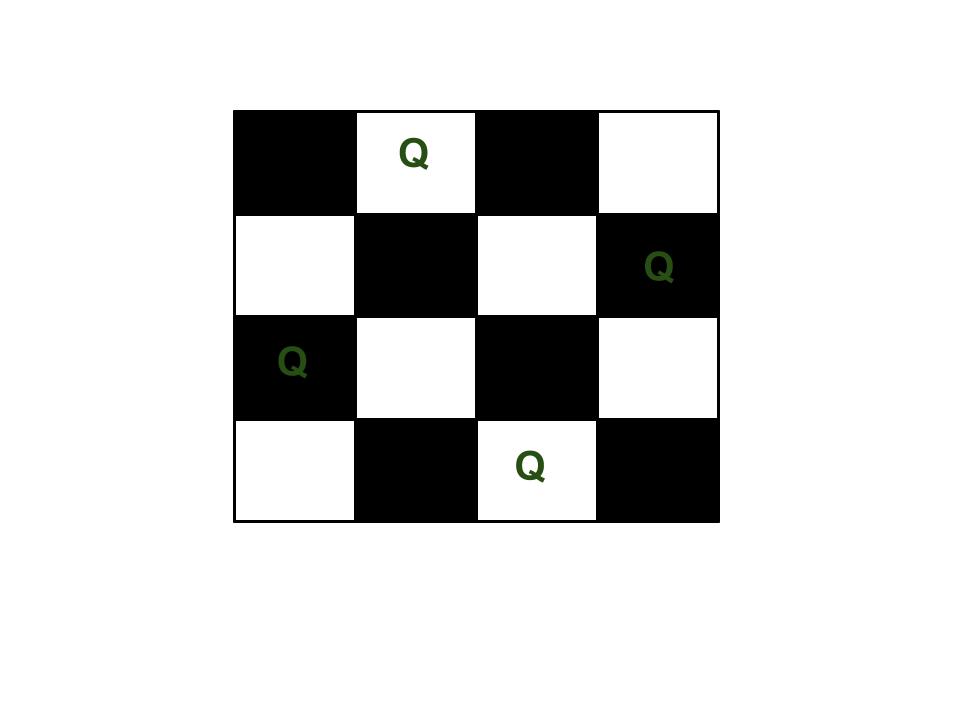
预期的输出是一个二进制矩阵, 其中放置了皇后的块的二进制数为1。例如, 以下是上述4个女王解决方案的输出矩阵。
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}推荐:请在"实践首先, 在继续解决方案之前。
天真的算法
在船上生成皇后区的所有可能配置, 并打印满足给定约束的配置。
while there are untried configurations
{
generate the next configuration
if queens don't attack in this configuration then
{
print this configuration;
}
}这个想法是将皇后区从最左边的列开始一个一列地放置在不同的列中。当我们在一个列中放置一个皇后时, 我们检查是否与已经放置的皇后发生冲突。在当前列中, 如果找到没有冲突的行, 则将该行和列标记为解决方案的一部分。如果由于冲突而找不到这样的行, 那么我们将回溯并返回false。
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column.
Do following for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing the queen in [row, column] leads to
a solution then return true.
c) If placing queen doesn't lead to a solution then
unmark this [row, column] (Backtrack) and go to
step (a) to try other rows.
3) If all rows have been tried and nothing worked, return false to trigger backtracking.回溯解决方案的实施
C / C ++
/* C/C++ program to solve N Queen Problem using
backtracking */
#define N 4
#include <stdbool.h>
#include <stdio.h>
/* A utility function to print solution */
void printSolution( int board[N][N])
{
for ( int i = 0; i < N; i++) {
for ( int j = 0; j < N; j++)
printf ( " %d " , board[i][j]);
printf ( "\n" );
}
}
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens */
bool isSafe( int board[N][N], int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0; i < col; i++)
if (board[row][i])
return false ;
/* Check upper diagonal on left side */
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j])
return false ;
/* Check lower diagonal on left side */
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j])
return false ;
return true ;
}
/* A recursive utility function to solve N
Queen problem */
bool solveNQUtil( int board[N][N], int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true ;
/* Consider this column and try placing
this queen in all rows one by one */
for ( int i = 0; i < N; i++) {
/* Check if the queen can be placed on
board[i][col] */
if (isSafe(board, i, col)) {
/* Place this queen in board[i][col] */
board[i][col] = 1;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1))
return true ;
/* If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] */
board[i][col] = 0; // BACKTRACK
}
}
/* If the queen cannot be placed in any row in
this colum col then return false */
return false ;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQ()
{
int board[N][N] = { { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false ) {
printf ( "Solution does not exist" );
return false ;
}
printSolution(board);
return true ;
}
// driver program to test above function
int main()
{
solveNQ();
return 0;
}Java
/* Java program to solve N Queen Problem using
backtracking */
public class NQueenProblem {
final int N = 4 ;
/* A utility function to print solution */
void printSolution( int board[][])
{
for ( int i = 0 ; i < N; i++) {
for ( int j = 0 ; j < N; j++)
System.out.print( " " + board[i][j]
+ " " );
System.out.println();
}
}
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are already
placeed in columns from 0 to col -1. So we need
to check only left side for attacking queens */
boolean isSafe( int board[][], int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0 ; i < col; i++)
if (board[row][i] == 1 )
return false ;
/* Check upper diagonal on left side */
for (i = row, j = col; i >= 0 && j >= 0 ; i--, j--)
if (board[i][j] == 1 )
return false ;
/* Check lower diagonal on left side */
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1 )
return false ;
return true ;
}
/* A recursive utility function to solve N
Queen problem */
boolean solveNQUtil( int board[][], int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true ;
/* Consider this column and try placing
this queen in all rows one by one */
for ( int i = 0 ; i < N; i++) {
/* Check if the queen can be placed on
board[i][col] */
if (isSafe(board, i, col)) {
/* Place this queen in board[i][col] */
board[i][col] = 1 ;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1 ) == true )
return true ;
/* If placing queen in board[i][col]
doesn't lead to a solution then
remove queen from board[i][col] */
board[i][col] = 0 ; // BACKTRACK
}
}
/* If the queen can not be placed in any row in
this colum col, then return false */
return false ;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil () to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
boolean solveNQ()
{
int board[][] = { { 0 , 0 , 0 , 0 }, { 0 , 0 , 0 , 0 }, { 0 , 0 , 0 , 0 }, { 0 , 0 , 0 , 0 } };
if (solveNQUtil(board, 0 ) == false ) {
System.out.print( "Solution does not exist" );
return false ;
}
printSolution(board);
return true ;
}
// driver program to test above function
public static void main(String args[])
{
NQueenProblem Queen = new NQueenProblem();
Queen.solveNQ();
}
}
// This code is contributed by Abhishek ShankhadharPython3
# Python3 program to solve N Queen
# Problem using backtracking
global N
N = 4
def printSolution(board):
for i in range (N):
for j in range (N):
print (board[i][j], end = " " )
print ()
# A utility function to check if a queen can
# be placed on board[row][col]. Note that this
# function is called when "col" queens are
# already placed in columns from 0 to col -1.
# So we need to check only left side for
# attacking queens
def isSafe(board, row, col):
# Check this row on left side
for i in range (col):
if board[row][i] = = 1 :
return False
# Check upper diagonal on left side
for i, j in zip ( range (row, - 1 , - 1 ), range (col, - 1 , - 1 )):
if board[i][j] = = 1 :
return False
# Check lower diagonal on left side
for i, j in zip ( range (row, N, 1 ), range (col, - 1 , - 1 )):
if board[i][j] = = 1 :
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed
# then return true
if col > = N:
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range (N):
if isSafe(board, i, col):
# Place this queen in board[i][col]
board[i][col] = 1
# recur to place rest of the queens
if solveNQUtil(board, col + 1 ) = = True :
return True
# If placing queen in board[i][col
# doesn't lead to a solution, then
# queen from board[i][col]
board[i][col] = 0
# if the queen can not be placed in any row in
# this colum col then return false
return False
# This function solves the N Queen problem using
# Backtracking. It mainly uses solveNQUtil() to
# solve the problem. It returns false if queens
# cannot be placed, otherwise return true and
# placement of queens in the form of 1s.
# note that there may be more than one
# solutions, this function prints one of the
# feasible solutions.
def solveNQ():
board = [ [ 0 , 0 , 0 , 0 ], [ 0 , 0 , 0 , 0 ], [ 0 , 0 , 0 , 0 ], [ 0 , 0 , 0 , 0 ] ]
if solveNQUtil(board, 0 ) = = False :
print ( "Solution does not exist" )
return False
printSolution(board)
return True
# Driver Code
solveNQ()
# This code is contributed by Divyanshu MehtaC#
// C# program to solve N Queen Problem
// using backtracking
using System;
class GFG
{
readonly int N = 4;
/* A utility function to print solution */
void printSolution( int [, ]board)
{
for ( int i = 0; i < N; i++)
{
for ( int j = 0; j < N; j++)
Console.Write( " " + board[i, j]
+ " " );
Console.WriteLine();
}
}
/* A utility function to check if a queen can
be placed on board[row, col]. Note that this
function is called when "col" queens are already
placeed in columns from 0 to col -1. So we need
to check only left side for attacking queens */
bool isSafe( int [, ]board, int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0; i < col; i++)
if (board[row, i] == 1)
return false ;
/* Check upper diagonal on left side */
for (i = row, j = col; i >= 0 &&
j >= 0; i--, j--)
if (board[i, j] == 1)
return false ;
/* Check lower diagonal on left side */
for (i = row, j = col; j >= 0 &&
i < N; i++, j--)
if (board[i, j] == 1)
return false ;
return true ;
}
/* A recursive utility function to solve N
Queen problem */
bool solveNQUtil( int [, ]board, int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true ;
/* Consider this column and try placing
this queen in all rows one by one */
for ( int i = 0; i < N; i++)
{
/* Check if the queen can be placed on
board[i, col] */
if (isSafe(board, i, col))
{
/* Place this queen in board[i, col] */
board[i, col] = 1;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1) == true )
return true ;
/* If placing queen in board[i, col]
doesn't lead to a solution then
remove queen from board[i, col] */
board[i, col] = 0; // BACKTRACK
}
}
/* If the queen can not be placed in any row in
this colum col, then return false */
return false ;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil () to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQ()
{
int [, ]board = {{ 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }};
if (solveNQUtil(board, 0) == false )
{
Console.Write( "Solution does not exist" );
return false ;
}
printSolution(board);
return true ;
}
// Driver Code
public static void Main(String []args)
{
GFG Queen = new GFG();
Queen.solveNQ();
}
}
// This code is contributed by Princi Singh输出如下:
1值表示皇后区的位置
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0is_safe()函数中的优化
这个想法不是检查左右对角线的每个元素, 而是使用对角线的属性:
1. i和j的和是恒定的, 并且对于每个右对角线都是唯一的, 其中i是元素的行, j是元素的行
元素列。
2. i和j的差是恒定的, 并且对于每个左对角线都是唯一的, 其中i和j分别是元素的行和列。
回溯解决方案的实现(优化)
C / C ++
/* C/C++ program to solve N Queen Problem using
backtracking */
#define N 4
#include <stdbool.h>
#include <stdio.h>
/* ld is an array where its indices indicate row-col+N-1
(N-1) is for shifting the difference to store negative
indices */
int ld[30] = { 0 };
/* rd is an array where its indices indicate row+col
and used to check whether a queen can be placed on
right diagonal or not*/
int rd[30] = { 0 };
/*column array where its indices indicates column and
used to check whether a queen can be placed in that
row or not*/
int cl[30] = { 0 };
/* A utility function to print solution */
void printSolution( int board[N][N])
{
for ( int i = 0; i < N; i++) {
for ( int j = 0; j < N; j++)
printf ( " %d " , board[i][j]);
printf ( "\n" );
}
}
/* A recursive utility function to solve N
Queen problem */
bool solveNQUtil( int board[N][N], int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true ;
/* Consider this column and try placing
this queen in all rows one by one */
for ( int i = 0; i < N; i++) {
/* Check if the queen can be placed on
board[i][col] */
/* A check if a queen can be placed on
board[row][col].We just need to check
ld[row-col+n-1] and rd[row+coln] where
ld and rd are for left and right
diagonal respectively*/
if ((ld[i - col + N - 1] != 1 &&
rd[i + col] != 1) && cl[i] != 1) {
/* Place this queen in board[i][col] */
board[i][col] = 1;
ld[i - col + N - 1] =
rd[i + col] = cl[i] = 1;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1))
return true ;
/* If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] */
board[i][col] = 0; // BACKTRACK
ld[i - col + N - 1] =
rd[i + col] = cl[i] = 0;
}
}
/* If the queen cannot be placed in any row in
this colum col then return false */
return false ;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
bool solveNQ()
{
int board[N][N] = { { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false ) {
printf ( "Solution does not exist" );
return false ;
}
printSolution(board);
return true ;
}
// driver program to test above function
int main()
{
solveNQ();
return 0;
}Java
/* Java program to solve N Queen Problem
using backtracking */
import java.util.*;
class GFG
{
static int N = 4 ;
/* ld is an array where its indices indicate row-col+N-1
(N-1) is for shifting the difference to store negative
indices */
static int []ld = new int [ 30 ];
/* rd is an array where its indices indicate row+col
and used to check whether a queen can be placed on
right diagonal or not*/
static int []rd = new int [ 30 ];
/*column array where its indices indicates column and
used to check whether a queen can be placed in that
row or not*/
static int []cl = new int [ 30 ];
/* A utility function to print solution */
static void printSolution( int board[][])
{
for ( int i = 0 ; i < N; i++)
{
for ( int j = 0 ; j < N; j++)
System.out.printf( " %d " , board[i][j]);
System.out.printf( "\n" );
}
}
/* A recursive utility function to solve N
Queen problem */
static boolean solveNQUtil( int board[][], int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true ;
/* Consider this column and try placing
this queen in all rows one by one */
for ( int i = 0 ; i < N; i++)
{
/* Check if the queen can be placed on
board[i][col] */
/* A check if a queen can be placed on
board[row][col].We just need to check
ld[row-col+n-1] and rd[row+coln] where
ld and rd are for left and right
diagonal respectively*/
if ((ld[i - col + N - 1 ] != 1 &&
rd[i + col] != 1 ) && cl[i] != 1 )
{
/* Place this queen in board[i][col] */
board[i][col] = 1 ;
ld[i - col + N - 1 ] =
rd[i + col] = cl[i] = 1 ;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1 ))
return true ;
/* If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] */
board[i][col] = 0 ; // BACKTRACK
ld[i - col + N - 1 ] =
rd[i + col] = cl[i] = 0 ;
}
}
/* If the queen cannot be placed in any row in
this colum col then return false */
return false ;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
static boolean solveNQ()
{
int board[][] = {{ 0 , 0 , 0 , 0 }, { 0 , 0 , 0 , 0 }, { 0 , 0 , 0 , 0 }, { 0 , 0 , 0 , 0 }};
if (solveNQUtil(board, 0 ) == false )
{
System.out.printf( "Solution does not exist" );
return false ;
}
printSolution(board);
return true ;
}
// Driver Code
public static void main(String[] args)
{
solveNQ();
}
}
// This code is contributed by Princi SinghPython3
""" Python3 program to solve N Queen Problem using
backtracking """
N = 4
""" ld is an array where its indices indicate row-col+N-1
(N-1) is for shifting the difference to store negative
indices """
ld = [ 0 ] * 30
""" rd is an array where its indices indicate row+col
and used to check whether a queen can be placed on
right diagonal or not"""
rd = [ 0 ] * 30
"""column array where its indices indicates column and
used to check whether a queen can be placed in that
row or not"""
cl = [ 0 ] * 30
""" A utility function to print solution """
def printSolution(board):
for i in range (N):
for j in range (N):
print (board[i][j], end = " " )
print ()
""" A recursive utility function to solve N
Queen problem """
def solveNQUtil(board, col):
""" base case: If all queens are placed
then return True """
if (col > = N):
return True
""" Consider this column and try placing
this queen in all rows one by one """
for i in range (N):
""" Check if the queen can be placed on board[i][col] """
""" A check if a queen can be placed on board[row][col].
We just need to check ld[row-col+n-1] and rd[row+coln]
where ld and rd are for left and right diagonal respectively"""
if ((ld[i - col + N - 1 ] ! = 1 and
rd[i + col] ! = 1 ) and cl[i] ! = 1 ):
""" Place this queen in board[i][col] """
board[i][col] = 1
ld[i - col + N - 1 ] = rd[i + col] = cl[i] = 1
""" recur to place rest of the queens """
if (solveNQUtil(board, col + 1 )):
return True
""" If placing queen in board[i][col]
doesn't lead to a solution, then remove queen from board[i][col] """
board[i][col] = 0 # BACKTRACK
ld[i - col + N - 1 ] = rd[i + col] = cl[i] = 0
""" If the queen cannot be placed in
any row in this colum col then return False """
return False
""" This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns False if queens
cannot be placed, otherwise, return True and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions."""
def solveNQ():
board = [[ 0 , 0 , 0 , 0 ], [ 0 , 0 , 0 , 0 ], [ 0 , 0 , 0 , 0 ], [ 0 , 0 , 0 , 0 ]]
if (solveNQUtil(board, 0 ) = = False ):
printf( "Solution does not exist" )
return False
printSolution(board)
return True
# Driver Code
solveNQ()
# This code is contributed by SHUBHAMSINGH10C#
/* C# program to solve N Queen Problem
using backtracking */
using System;
class GFG
{
static int N = 4;
/* ld is an array where its indices indicate row-col+N-1
(N-1) is for shifting the difference to store negative
indices */
static int []ld = new int [30];
/* rd is an array where its indices indicate row+col
and used to check whether a queen can be placed on
right diagonal or not*/
static int []rd = new int [30];
/*column array where its indices indicates column and
used to check whether a queen can be placed in that
row or not*/
static int []cl = new int [30];
/* A utility function to print solution */
static void printSolution( int [, ]board)
{
for ( int i = 0; i < N; i++)
{
for ( int j = 0; j < N; j++)
Console.Write( " {0} " , board[i, j]);
Console.Write( "\n" );
}
}
/* A recursive utility function to solve N
Queen problem */
static bool solveNQUtil( int [, ]board, int col)
{
/* base case: If all queens are placed
then return true */
if (col >= N)
return true ;
/* Consider this column and try placing
this queen in all rows one by one */
for ( int i = 0; i < N; i++)
{
/* Check if the queen can be placed on
board[i, col] */
/* A check if a queen can be placed on
board[row, col].We just need to check
ld[row-col+n-1] and rd[row+coln] where
ld and rd are for left and right
diagonal respectively*/
if ((ld[i - col + N - 1] != 1 &&
rd[i + col] != 1) && cl[i] != 1)
{
/* Place this queen in board[i, col] */
board[i, col] = 1;
ld[i - col + N - 1] =
rd[i + col] = cl[i] = 1;
/* recur to place rest of the queens */
if (solveNQUtil(board, col + 1))
return true ;
/* If placing queen in board[i, col]
doesn't lead to a solution, then
remove queen from board[i, col] */
board[i, col] = 0; // BACKTRACK
ld[i - col + N - 1] =
rd[i + col] = cl[i] = 0;
}
}
/* If the queen cannot be placed in any row in
this colum col then return false */
return false ;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise, return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
static bool solveNQ()
{
int [, ]board = {{ 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }, { 0, 0, 0, 0 }};
if (solveNQUtil(board, 0) == false )
{
Console.Write( "Solution does not exist" );
return false ;
}
printSolution(board);
return true ;
}
// Driver Code
public static void Main(String[] args)
{
solveNQ();
}
}
// This code is contributed by Rajput-Ji输出如下:
1值表示皇后区的位置
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0打印N皇后问题中的所有解决方案
资料来源:
http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf
http://en.literateprograms.org/Eight_queens_puzzle_%28C%29
http://en.wikipedia.org/wiki/Eight_queens_puzzle
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)