算法题：最长回文子串的长度

2021年4月27日17:08:00 发表评论 1,042 次浏览

本文概述

给定一个字符串小号长度ñ, 任务是找到最长回文子串从给定的字符串。

例子：

输入：S ="abcbab"
输出：5
说明：字符串" abcba"是最长的子字符串, 是回文, 长度为5。
输入：S ="abcdaa"
输出：2
说明：字符串" aa"是最长的子字符串那是回文长度为2的回文。

简单的方法：解决问题的最简单方法是生成给定字符串的所有可能的子字符串并打印长度最长子串这是一个回文.

下面是上述方法的实现：

C ++

//C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
//Function to obtain the length of
//the longest palindromic substring
int longestPalSubstr(string str)
{
     //Length of given string
     int n = str.size();
 
     //Stores the maximum length
     int maxLength = 1, start = 0;
 
     //Iterate over the string
     for ( int i = 0;
          i <str.length(); i++) {
 
         //Iterate over the string
         for ( int j = i;
              j <str.length(); j++) {
             int flag = 1;
 
             //Check for palindrome
             for ( int k = 0;
                  k <(j - i + 1) /2; k++)
                 if (str[i + k]
                     != str[j - k])
                     flag = 0;
 
             //If string [i, j - i + 1]
             //is palindromic
             if (flag
                 && (j - i + 1)> maxLength) {
                 start = i;
                 maxLength = j - i + 1;
             }
         }
     }
 
     //Return length of LPS
     return maxLength;
}
 
//Driver Code
int main()
{
     //Given string
     string str = "forgeeksskeegfor" ;
 
     //Function Call
     cout <<longestPalSubstr(str);
     return 0;
}

Java

//Java program for the above approach
import java.io.*;
 
class GFG{
  
//Function to obtain the length of
//the longest palindromic substring
static int longestPalSubstr(String str)
{
     
     //Length of given string
     int n = str.length();
  
     //Stores the maximum length
     int maxLength = 1 , start = 0 ;
  
     //Iterate over the string
     for ( int i = 0 ; i <str.length(); i++)
     {
         
         //Iterate over the string
         for ( int j = i; j <str.length(); j++)
         {
             int flag = 1 ;
  
             //Check for palindrome
             for ( int k = 0 ;
                     k <(j - i + 1 ) /2 ; k++)
                 if (str.charAt(i + k) !=
                     str.charAt(j - k))
                     flag = 0 ;
  
             //If string [i, j - i + 1]
             //is palindromic
             if (flag != 0 &&
                (j - i + 1 )> maxLength)
             {
                 start = i;
                 maxLength = j - i + 1 ;
             }
         }
     }
  
     //Return length of LPS
     return maxLength;
}
  
//Driver Code
public static void main (String[] args)
{
     
     //Given string
     String str = "forgeeksskeegfor" ;
  
     //Function call
     System.out.print(longestPalSubstr(str));
}
}
 
//This code is contributed by code_hunt

Python3

# Python3 program for the above approach
 
# Function to obtain the length of
# the longest palindromic substring
def longestPalSubstr( str ):
     
     # Length of given string
     n = len ( str )
  
     # Stores the maximum length
     maxLength = 1
     start = 0
  
     # Iterate over the string
     for i in range ( len ( str )):
  
         # Iterate over the string
         for j in range (i, len ( str ), 1 ):
             flag = 1
  
             # Check for palindrome
             for k in range ((j - i + 1 ) //2 ):
                 if ( str [i + k] ! = str [j - k]):
                     flag = 0
  
             # If string [i, j - i + 1]
             # is palindromic
             if (flag ! = 0 and
                (j - i + 1 )> maxLength):
                 start = i
                 maxLength = j - i + 1
             
     # Return length of LPS
     return maxLength
 
# Driver Code
 
# Given string
str = "forgeeksskeegfor"
  
# Function call
print (longestPalSubstr( str ))
 
# This code is contributed by code_hunt

C#

//C# program for the above approach 
using System;
 
class GFG{
  
//Function to obtain the length of
//the longest palindromic substring
static int longestPalSubstr( string str)
{
     
     //Length of given string
     int n = str.Length;
  
     //Stores the maximum length
     int maxLength = 1, start = 0;
  
     //Iterate over the string
     for ( int i = 0; i <str.Length; i++)
     {
         
         //Iterate over the string
         for ( int j = i; j <str.Length; j++)
         {
             int flag = 1;
  
             //Check for palindrome
             for ( int k = 0;
                     k <(j - i + 1) /2; k++)
                 if (str[i + k] != str[j - k])
                     flag = 0;
  
             //If string [i, j - i + 1]
             //is palindromic
             if (flag != 0 &&
                (j - i + 1)> maxLength)
             {
                 start = i;
                 maxLength = j - i + 1;
             }
         }
     }
  
     //Return length of LPS
     return maxLength;
}
  
//Driver Code
public static void Main ()
{
     
     //Given string
     string str = "forgeeksskeegfor" ;
  
     //Function call
     Console.Write(longestPalSubstr(str));
}
}
 
//This code is contributed by code_hunt

输出如下：

10

时间复杂度：O(N^3), 其中N是给定字符串的长度。

辅助空间：O(N)

动态规划方法：通过存储以下结果可以优化上述方法重叠子问题。这个想法类似于这个帖子。步骤如下：

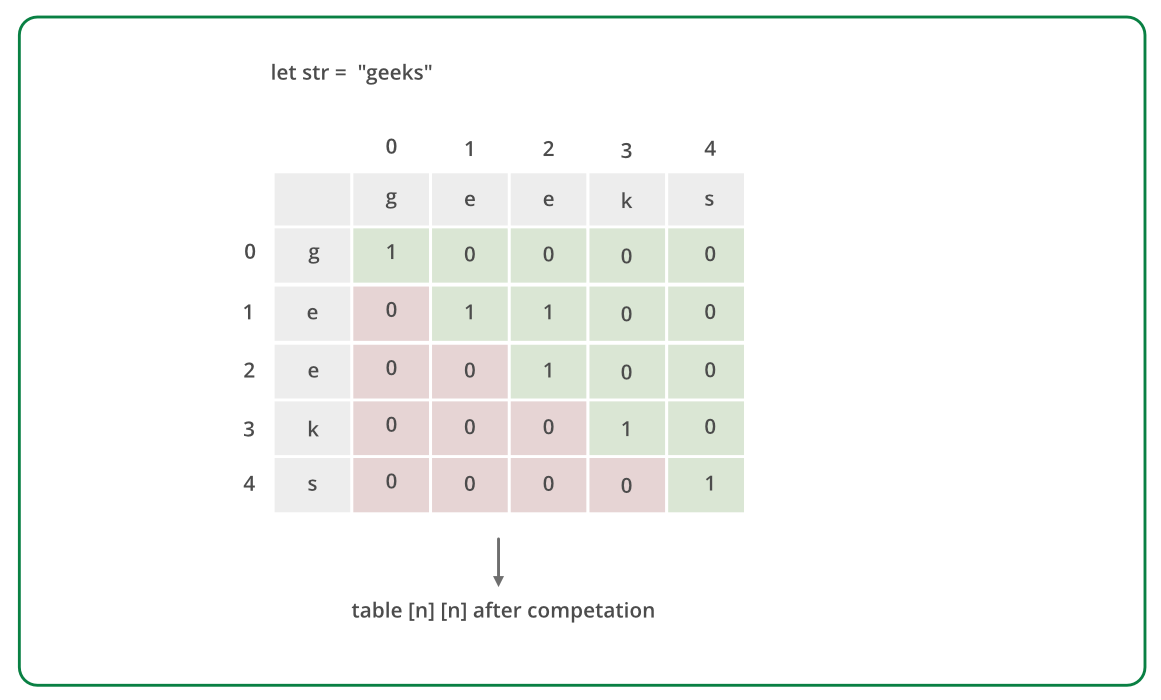
  1. 维护一个布尔表table[N][N]，以自底向上的方式填充。
  2. 如果子字符串是回文，表table[i][j]的值为true，否则为false。
  3. 计算表table[i][j]，检查表table[i + 1][j - 1]的值，如果值为true且str[i]与str[j]相同，则更新表table[i][j]的值为true。
  4. 否则, 表table[i] [j]的值被更新为false。

下面是字符串的插图"geeks":

最长回文子串的长度1

下面是上述方法的实现：

C ++

//C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
//Function to find the length of
//the longest palindromic substring
int longestPalSubstr(string str)
{
     //Length of string str
     int n = str.size();
 
     //Stores the dp states
     bool table[n][n];
 
     //Initialise table[][] as false
     memset (table, 0, sizeof (table));
 
     //All substrings of length 1
     //are palindromes
     int maxLength = 1;
 
     for ( int i = 0; i <n; ++i)
         table[i][i] = true ;
 
     //Check for sub-string of length 2
     int start = 0;
 
     for ( int i = 0; i <n - 1; ++i) {
 
         //If adjacent character are same
         if (str[i] == str[i + 1]) {
 
             //Update table[i][i + 1]
             table[i][i + 1] = true ;
             start = i;
             maxLength = 2;
         }
     }
 
     //Check for lengths greater than 2
     //k is length of substring
     for ( int k = 3; k <= n; ++k) {
 
         //Fix the starting index
         for ( int i = 0; i <n - k + 1; ++i) {
 
             //Ending index of substring
             //of length k
             int j = i + k - 1;
 
             //Check for palindromic
             //substring str[i, j]
             if (table[i + 1][j - 1]
                 && str[i] == str[j]) {
 
                 //Mark true
                 table[i][j] = true ;
 
                 //Update the maximum length
                 if (k> maxLength) {
                     start = i;
                     maxLength = k;
                 }
             }
         }
     }
 
     //Return length of LPS
     return maxLength;
}
 
//Driver Code
int main()
{
     //Given string str
     string str = "forgeeksskeegfor" ;
 
     //Function Call
     cout <<longestPalSubstr(str);
 
     return 0;
}

Java

//Java program for the above approach
import java.util.*;
 
class GFG{
 
//Function to find the length of
//the longest palindromic subString
static int longestPalSubstr(String str)
{
     
     //Length of String str
     int n = str.length();
 
     //Stores the dp states
     boolean [][]table = new boolean [n][n];
 
     //All subStrings of length 1
     //are palindromes
     int maxLength = 1 ;
 
     for ( int i = 0 ; i <n; ++i)
         table[i][i] = true ;
 
     //Check for sub-String of length 2
     int start = 0 ;
 
     for ( int i = 0 ; i <n - 1 ; ++i)
     {
         
         //If adjacent character are same
         if (str.charAt(i) == str.charAt(i + 1 ))
         {
             
             //Update table[i][i + 1]
             table[i][i + 1 ] = true ;
             start = i;
             maxLength = 2 ;
         }
     }
 
     //Check for lengths greater than 2
     //k is length of subString
     for ( int k = 3 ; k <= n; ++k)
     {
         
         //Fix the starting index
         for ( int i = 0 ; i <n - k + 1 ; ++i)
         {
             
             //Ending index of subString
             //of length k
             int j = i + k - 1 ;
 
             //Check for palindromic
             //subString str[i, j]
             if (table[i + 1 ][j - 1 ] &&
                 str.charAt(i) == str.charAt(j))
             {
                 
                 //Mark true
                 table[i][j] = true ;
 
                 //Update the maximum length
                 if (k> maxLength)
                 {
                     start = i;
                     maxLength = k;
                 }
             }
         }
     }
     
     //Return length of LPS
     return maxLength;
}
 
//Driver Code
public static void main(String[] args)
{
     
     //Given String str
     String str = "forgeeksskeegfor" ;
 
     //Function Call
     System.out.print(longestPalSubstr(str));
}
}
 
//This code is contributed by Amit Katiyar

C#

//C# program for
//the above approach
using System;
class GFG{
 
//Function to find the length of
//the longest palindromic subString
static int longestPalSubstr(String str)
{
   //Length of String str
   int n = str.Length;
 
   //Stores the dp states
   bool [, ]table = new bool [n, n];
 
   //All subStrings of length 1
   //are palindromes
   int maxLength = 1;
 
   for ( int i = 0; i <n; ++i)
     table[i, i] = true ;
 
   //Check for sub-String
   //of length 2
   int start = 0;
 
   for ( int i = 0; i <n - 1; ++i)
   {
     //If adjacent character are same
     if (str[i] == str[i + 1])
     {
       //Update table[i, i + 1]
       table[i, i + 1] = true ;
       start = i;
       maxLength = 2;
     }
   }
 
   //Check for lengths greater than 2
   //k is length of subString
   for ( int k = 3; k <= n; ++k)
   {
     //Fix the starting index
     for ( int i = 0; i <n - k + 1; ++i)
     {
       //Ending index of subString
       //of length k
       int j = i + k - 1;
 
       //Check for palindromic
       //subString str[i, j]
       if (table[i + 1, j - 1] &&
           str[i] == str[j])
       {
         //Mark true
         table[i, j] = true ;
 
         //Update the maximum length
         if (k> maxLength)
         {
           start = i;
           maxLength = k;
         }
       }
     }
   }
 
   //Return length of LPS
   return maxLength;
}
 
//Driver Code
public static void Main(String[] args)
{
   //Given String str
   String str = "forgeeksskeegfor" ;
 
   //Function Call
   Console.Write(longestPalSubstr(str));
}
}
 
//This code is contributed by Rajput-Ji

Python3

# Python program for the above approach
 
 
# Function to find the length of
# the longest palindromic subString
def longestPalSubstr( str ):
     # Length of String str
     n = len ( str );
 
     # Stores the dp states
     table = [[ False for i in range (n)] for j in range (n)];
 
     # All subStrings of length 1
     # are palindromes
     maxLength = 1 ;
 
     for i in range (n):
         table[i][i] = True ;
 
     # Check for sub-String of length 2
     start = 0 ;
 
     for i in range (n - 1 ):
 
         # If adjacent character are same
         if ( str [i] = = str [i + 1 ]):
             # Update table[i][i + 1]
             table[i][i + 1 ] = True ;
             start = i;
             maxLength = 2 ;
 
     # Check for lengths greater than 2
     # k is length of subString
     for k in range ( 3 , n + 1 ):
 
         # Fix the starting index
         for i in range (n - k + 1 ):
 
             # Ending index of subString
             # of length k
             j = i + k - 1 ;
 
             # Check for palindromic
             # subString str[i, j]
             if (table[i + 1 ][j - 1 ] and str [i] = = str [j]):
 
                 # Mark True
                 table[i][j] = True ;
 
                 # Update the maximum length
                 if (k> maxLength):
                     start = i;
                     maxLength = k;
 
     # Return length of LPS
     return maxLength;
 
 
# Driver Code
if __name__ = = '__main__' :
     # Given String str
     str = "forgeeksskeegfor" ;
 
     # Function Call
     print (longestPalSubstr( str ));
 
# This code is contributed by 29AjayKumar

输出如下：

10

时间复杂度：O(N^2), 其中N是给定字符串的长度。

辅助空间：O(N))

高效方法：为了优化上述方法, 想法是使用经理的算法。通过使用此算法, 对于每个字符C, 最长的回文子串具有C因为它的中心长度是奇数。但是最长的回文子串也可以具有均匀的长度, 没有任何中心。因此, 可以在每个字符之间添加一些特殊字符。

例如, 如果给定的字符串是" abababc", 则它将变为" $＃a＃b＃a＃b＃a＃b＃c＃@"。现在, 请注意, 在这种情况下, 对于每个字符c, 以c为中心的最长回文子字符串的长度将为奇数。

步骤如下：

  1. 在给定的字符串中添加特殊字符小号如上所述, 让它的长度为ñ.
  2. 初始化数组d [], 中心和[R与0其中d [i]存储回文的左侧部分的长度, 其中S [i]是中心[R表示最右边的访问边界, 而center表示当前字符索引, 它是此最右边边界的中心。
  3. 在遍历字符串时小号, 对于每个索引一世如果我小于r那么它的答案就已经被计算过了d [i]可以设置为等于回答字符镜像一世中心可以计算为(2 *中心– i).
  4. 现在, 检查r后面是否有某些字符, 以使回文变得越来越长。
  5. If(i + d [i])大于r, 更新r =(i + d [i])并以一世.
  6. 在找到每个角色最长的回文之后C作为中心, 打印最大值(2 * d [i] +1)/ 2其中0≤i <N因为d [i]仅存储回文的左侧部分。

下面是上述方法的实现：

Python3

# Python program for the above approach
 
# Function that placed '#' intermediately
# before and after each character
def UpdatedString(string):
 
     newString = [ '#' ]
 
# Traverse the string
     for char in string:
         newString + = [char, '#' ]
 
# Return the string
     return ''.join(newString)
 
# Function that finds the length of
# the longest palindromic substring
def Manacher(string):
 
     # Update the string
     string = UpdatedString(string)
 
     # Stores the longest proper prefix
     # which is also a suffix
     LPS = [ 0 for _ in range ( len (string))]
     C = 0
     R = 0
 
     for i in range ( len (string)):
         imir = 2 * C - i
 
         # Find the minimum length of
         # the palindrome
         if R> i:
             LPS[i] = min (R - i, LPS[imir])
         else :
 
             # Find the actual length of
             # the palindrome
             LPS[i] = 0
 
         # Exception Handling
         try :
             while string[i + 1 + LPS[i]] \
             = = string[i - 1 - LPS[i]]:
                 LPS[i] + = 1
         except :
             pass
 
         # Update C and R
         if i + LPS[i]> R:
             C = i
             R = i + LPS[i]
 
     r, c = max (LPS), LPS.index( max (LPS))
 
     # Return the length r
     return r
 
 
# Driver code
 
# Given string str
str = "forgeeksskeegfor"
 
# Function Call
print (Manacher( str ))

输出如下：

10

时间复杂度：O(N), 其中N是给定字符串的长度。

辅助空间：O(N)

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: