算法题：直方图中最大的矩形区域|S2

2021年4月19日12:20:38 发表评论 972 次浏览

本文概述

C ++
Java
Python3
C#

在给定的直方图中找到最大的矩形区域, 其中最大的矩形可以由许多连续的条形组成。为简单起见, 假定所有条形都具有相同的宽度, 并且宽度为1个单位。

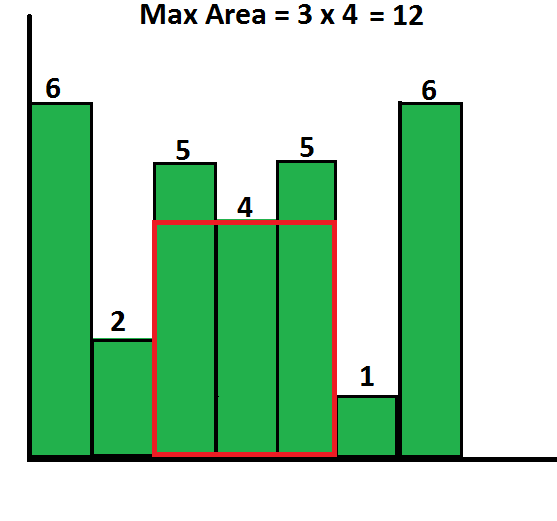
例如, 考虑以下具有7个高度{6, 2, 5, 4, 4, 5, 1, 6}的条形图。可能的最大矩形是12(请参见下图, 最大面积的矩形以红色突出显示)

我们已经讨论了基于分治法的O(nLogn)解决方案

对于这个问题。在这篇文章中, 讨论了O(n)时间解。像以前的帖子, 为简单起见, 所有条的宽度假定为1。对于每个" x"条, 我们以" x"作为矩形中最小的条计算面积。如果我们为每个小节" x"计算这样的面积并找到所有面积的最大值, 那么我们的任务就完成了。如何以" x"作为最小条形来计算面积？我们需要知道" x"左侧第一个较小(小于" x")条的索引, 以及" x"右侧第一个较小的索引。让我们将这些索引分别称为"左索引"和"右索引"。

我们从左到右遍历所有条, 并保持一堆条。每个条被推入堆栈一次。当看到较小高度的条时, 将从堆栈中弹出条。弹出条时, 我们以弹出条为最小条来计算面积。我们如何获得弹出栏的左右索引-当前索引告诉我们"右索引", 而堆栈中上一项的索引就是"左索引"。以下是完整的算法。

1)创建一个空堆栈。

2)从第一个小节开始, 然后对每个小节" hist [i]"执行跟踪, 其中" i"的范围从0到n-1。

……a)如果堆栈为空或hist [i]高于堆栈顶部的条, 则按" i"进行堆栈。

……b)如果此栏小于堆栈顶部, 则在堆栈顶部较大的同时, 继续移除堆栈顶部。令删除的条为hist [tp]。用hist [tp]作为最小条形来计算矩形的面积。对于hist [tp], "左索引"是堆栈中的上一个项目(在tp之前), "右索引"是" i"(当前索引)。

3)如果堆栈不是空的, 则一个接一个地从堆栈中删除所有条, 并对每个已删除的条执行步骤2.b。

以下是上述算法的实现。

C ++

//C++ program to find maximum rectangular area in
//linear time
#include<bits/stdc++.h>
using namespace std;
  
//The main function to find the maximum rectangular 
//area under given histogram with n bars
int getMaxArea( int hist[], int n)
{
     //Create an empty stack. The stack holds indexes 
     //of hist[] array. The bars stored in stack are 
     //always in increasing order of their heights.
     stack<int> s;
  
     int max_area = 0; //Initialize max area
     int tp;  //To store top of stack
     int area_with_top; //To store area with top bar
                        //as the smallest bar
  
     //Run through all bars of given histogram
     int i = 0;
     while (i <n)
     {
         //If this bar is higher than the bar on top 
         //stack, push it to stack
         if (s.empty() || hist[s.top()] <= hist[i])
             s.push(i++);
  
         //If this bar is lower than top of stack, //then calculate area of rectangle with stack 
         //top as the smallest (or minimum height) bar. 
         //'i' is 'right index' for the top and element 
         //before top in stack is 'left index'
         else
         {
             tp = s.top();  //store the top index
             s.pop();  //pop the top
  
             //Calculate the area with hist[tp] stack 
             //as smallest bar
             area_with_top = hist[tp] * (s.empty() ? i : 
                                    i - s.top() - 1);
  
             //update max area, if needed
             if (max_area <area_with_top)
                 max_area = area_with_top;
         }
     }
  
     //Now pop the remaining bars from stack and calculate
     //area with every popped bar as the smallest bar
     while (s.empty() == false )
     {
         tp = s.top();
         s.pop();
         area_with_top = hist[tp] * (s.empty() ? i : 
                                 i - s.top() - 1);
  
         if (max_area <area_with_top)
             max_area = area_with_top;
     }
  
     return max_area;
}
  
//Driver program to test above function
int main()
{
     int hist[] = {6, 2, 5, 4, 5, 1, 6};
     int n = sizeof (hist)/sizeof (hist[0]);
     cout <<"Maximum area is " <<getMaxArea(hist, n);
     return 0;
}

Java

//Java program to find maximum rectangular area in linear time
  
import java.util.Stack;
  
public class RectArea 
{
     //The main function to find the maximum rectangular area under given
     //histogram with n bars
     static int getMaxArea( int hist[], int n) 
     {
         //Create an empty stack. The stack holds indexes of hist[] array
         //The bars stored in stack are always in increasing order of their
         //heights.
         Stack<Integer> s = new Stack<>();
          
         int max_area = 0 ; //Initialize max area
         int tp;  //To store top of stack
         int area_with_top; //To store area with top bar as the smallest bar
       
         //Run through all bars of given histogram
         int i = 0 ;
         while (i <n)
         {
             //If this bar is higher than the bar on top stack, push it to stack
             if (s.empty() || hist[s.peek()] <= hist[i])
                 s.push(i++);
       
             //If this bar is lower than top of stack, then calculate area of rectangle 
             //with stack top as the smallest (or minimum height) bar. 'i' is 
             //'right index' for the top and element before top in stack is 'left index'
             else
             {
                 tp = s.peek();  //store the top index
                 s.pop();  //pop the top
       
                 //Calculate the area with hist[tp] stack as smallest bar
                 area_with_top = hist[tp] * (s.empty() ? i : i - s.peek() - 1 );
       
                 //update max area, if needed
                 if (max_area <area_with_top)
                     max_area = area_with_top;
             }
         }
       
         //Now pop the remaining bars from stack and calculate area with every
         //popped bar as the smallest bar
         while (s.empty() == false )
         {
             tp = s.peek();
             s.pop();
             area_with_top = hist[tp] * (s.empty() ? i : i - s.peek() - 1 );
       
             if (max_area <area_with_top)
                 max_area = area_with_top;
         }
       
         return max_area;
  
     }
      
     //Driver program to test above function
     public static void main(String[] args) 
     {
         int hist[] = { 6 , 2 , 5 , 4 , 5 , 1 , 6 };
         System.out.println( "Maximum area is " + getMaxArea(hist, hist.length));
     }
}
//This code is Contributed by Sumit Ghosh

Python3

# Python3 program to find maximum 
# rectangular area in linear time
  
def max_area_histogram(histogram):
      
     # This function calulates maximum 
     # rectangular area under given 
     # histogram with n bars
  
     # Create an empty stack. The stack 
     # holds indexes of histogram[] list. 
     # The bars stored in the stack are
     # always in increasing order of 
     # their heights.
     stack = list ()
  
     max_area = 0 # Initialize max area
  
     # Run through all bars of
     # given histogram
     index = 0
     while index <len (histogram):
          
         # If this bar is higher 
         # than the bar on top
         # stack, push it to stack
  
         if ( not stack) or (histogram[stack[ - 1 ]] <= histogram[index]):
             stack.append(index)
             index + = 1
  
         # If this bar is lower than top of stack, # then calculate area of rectangle with 
         # stack top as the smallest (or minimum
         # height) bar.'i' is 'right index' for 
         # the top and element before top in stack
         # is 'left index'
         else :
             # pop the top
             top_of_stack = stack.pop()
  
             # Calculate the area with 
             # histogram[top_of_stack] stack
             # as smallest bar
             area = (histogram[top_of_stack] * 
                    ((index - stack[ - 1 ] - 1 ) 
                    if stack else index))
  
             # update max area, if needed
             max_area = max (max_area, area)
  
     # Now pop the remaining bars from 
     # stack and calculate area with 
     # every popped bar as the smallest bar
     while stack:
          
         # pop the top
         top_of_stack = stack.pop()
  
         # Calculate the area with 
         # histogram[top_of_stack] 
         # stack as smallest bar
         area = (histogram[top_of_stack] * 
               ((index - stack[ - 1 ] - 1 ) 
                 if stack else index))
  
         # update max area, if needed
         max_area = max (max_area, area)
  
     # Return maximum area under 
     # the given histogram
     return max_area
  
# Driver Code
hist = [ 6 , 2 , 5 , 4 , 5 , 1 , 6 ]
print ( "Maximum area is" , max_area_histogram(hist))
  
# This code is contributed 
# by Jinay Shah

C#

//C# program to find maximum 
//rectangular area in linear time 
using System;
using System.Collections.Generic;
  
class GFG
{
//The main function to find the 
//maximum rectangular area under 
//given histogram with n bars 
public static int getMaxArea( int [] hist, int n)
{
     //Create an empty stack. The stack 
     //holds indexes of hist[] array 
     //The bars stored in stack are always 
     //in increasing order of their heights. 
     Stack<int> s = new Stack<int>();
  
     int max_area = 0; //Initialize max area
     int tp; //To store top of stack
     int area_with_top; //To store area with top 
                        //bar as the smallest bar
  
     //Run through all bars of
     //given histogram 
     int i = 0;
     while (i <n)
     {
         //If this bar is higher than the 
         //bar on top stack, push it to stack 
         if (s.Count == 0 || hist[s.Peek()] <= hist[i])
         {
             s.Push(i++);
         }
  
         //If this bar is lower than top of stack, //then calculate area of rectangle with 
         //stack top as the smallest (or minimum  
         //height) bar. 'i' is 'right index' for 
         //the top and element before top in stack
         //is 'left index' 
         else
         {
             tp = s.Peek(); //store the top index
             s.Pop(); //pop the top
  
             //Calculate the area with hist[tp]
             //stack as smallest bar 
             area_with_top = hist[tp] * 
                            (s.Count == 0 ? i : i - s.Peek() - 1);
  
             //update max area, if needed 
             if (max_area <area_with_top)
             {
                 max_area = area_with_top;
             }
         }
     }
  
     //Now pop the remaining bars from 
     //stack and calculate area with every 
     //popped bar as the smallest bar 
     while (s.Count> 0)
     {
         tp = s.Peek();
         s.Pop();
         area_with_top = hist[tp] * 
                        (s.Count == 0 ? i : i - s.Peek() - 1);
  
         if (max_area <area_with_top)
         {
             max_area = area_with_top;
         }
     }
  
     return max_area;
  
}
  
//Driver Code
public static void Main( string [] args)
{
     int [] hist = new int [] {6, 2, 5, 4, 5, 1, 6};
     Console.WriteLine( "Maximum area is " + 
                        getMaxArea(hist, hist.Length));
}
}
  
//This code is contributed by Shrikant13

输出如下：