可能的二叉搜索树和具有n个键的二叉树的总数

2021年4月15日19:06:05 发表评论 986 次浏览

本文概述

具有n个不同键的可能二进制搜索树总数(countBST(n))=加泰罗尼亚语编号Cn=(2n)! /((n + 1)!* n!)

对于n = 0、1、2、3, ..., 加泰罗尼亚语值的值为1、1、2、5、14、42、132、429、1430、4862...。二叉搜索树的数目也是如此。

具有n个不同密钥的可能二叉树总数(countBT(n))= countBST(n)* n!

下面的代码用于查找具有n个数字的BST和二叉树的计数。查找第n个加泰罗尼亚语代码的代码取自这里.

C++

//See https://www.lsbin.org/program-nth-catalan-number/
//for reference of below code.
  
#include <bits/stdc++.h>
using namespace std;
  
//A function to find factorial of a given number
unsigned long int factorial(unsigned int n)
{
     unsigned long int res = 1;
  
     //Calculate value of [1*(2)*---*(n-k+1)] /[k*(k-1)*---*1]
     for ( int i = 1; i <= n; ++i)
     {
         res *= i;
     }
  
     return res;
}
  
unsigned long int binomialCoeff(unsigned int n, unsigned int k)
{
     unsigned long int res = 1;
  
     //Since C(n, k) = C(n, n-k)
     if (k> n - k)
         k = n - k;
  
     //Calculate value of [n*(n-1)*---*(n-k+1)] /[k*(k-1)*---*1]
     for ( int i = 0; i <k; ++i)
     {
         res *= (n - i);
         res /= (i + 1);
     }
  
     return res;
}
  
  
//A Binomial coefficient based function to find nth catalan
//number in O(n) time
unsigned long int catalan(unsigned int n)
{
     //Calculate value of 2nCn
     unsigned long int c = binomialCoeff(2*n, n);
  
     //return 2nCn/(n+1)
     return c/(n+1);
}
  
//A function to count number of BST with n nodes 
//using catalan
unsigned long int countBST(unsigned int n)
{
     //find nth catalan number
     unsigned long int count = catalan(n);
  
     //return nth catalan number
     return count;
}
  
//A function to count number of binary trees with n nodes 
unsigned long int countBT(unsigned int n)
{
     //find count of BST with n numbers
     unsigned long int count = catalan(n);
  
     //return count * n!
     return count * factorial(n);
}
  
//Driver Program to test above functions
int main()
{
  
     int count1, count2, n = 5;
  
     //find count of BST and binary trees with n nodes
         count1 = countBST(n);
         count2 = countBT(n); 
      
     //print count of BST and binary trees with n nodes
     cout<<"Count of BST with " <<n<<" nodes is " <<count1<<endl;
         cout<<"Count of binary trees with " <<n<<" nodes is " <<count2;
  
     return 0;
}

Java

//See https://www.lsbin.org/program-nth-catalan-number/
//for reference of below code.
import java.io.*;
  
class GFG 
{
      
//A function to find 
//factorial of a given number
static int factorial( int n)
{
     int res = 1 ;
  
     //Calculate value of 
     //[1*(2)*---*(n-k+1)] /
     //[k*(k-1)*---*1]
     for ( int i = 1 ; i <= n; ++i)
     {
         res *= i;
     }
  
     return res;
}
  
static int binomialCoeff( int n, int k)
{
     int res = 1 ;
  
     //Since C(n, k) = C(n, n-k)
     if (k> n - k)
         k = n - k;
  
     //Calculate value of 
     //[n*(n-1)*---*(n-k+1)] /
     //[k*(k-1)*---*1]
     for ( int i = 0 ; i <k; ++i)
     {
         res *= (n - i);
         res /= (i + 1 );
     }
  
     return res;
}
  
  
//A Binomial coefficient 
//based function to find 
//nth catalan number in 
//O(n) time
static int catalan( int n)
{
      
     //Calculate value of 2nCn
     int c = binomialCoeff( 2 * n, n);
  
     //return 2nCn/(n+1)
     return c /(n + 1 );
}
  
//A function to count number of
//BST with n nodes using catalan
static int countBST( int n)
{
     //find nth catalan number
     int count = catalan(n);
  
     //return nth catalan number
     return count;
}
  
//A function to count number
//of binary trees with n nodes 
static int countBT( int n)
{
     //find count of BST
     //with n numbers
     int count = catalan(n);
  
     //return count * n!
     return count * factorial(n);
}
  
//Driver Code
public static void main (String[] args)
{
     int count1, count2, n = 5 ;
  
     //find count of BST and 
     //binary trees with n nodes
     count1 = countBST(n);
     count2 = countBT(n); 
  
     //print count of BST and 
     //binary trees with n nodes
     System.out.println( "Count of BST with " + 
                             n + " nodes is " + 
                                     count1);
     System.out.println( "Count of binary " + 
                              "trees with " + 
                          n + " nodes is " + 
                                    count2);
}
}
  
//This code is contributed by ajit

Python3

# See https:#www.lsbin.org/program-nth-catalan-number/
# for reference of below code. 
  
# A function to find factorial of a given number 
def factorial(n) :
     res = 1
      
     # Calculate value of [1*(2)*---*
     #(n-k+1)] /[k*(k-1)*---*1] 
     for i in range ( 1 , n + 1 ): 
         res * = i 
     return res 
  
def binomialCoeff(n, k): 
  
     res = 1
  
     # Since C(n, k) = C(n, n-k) 
     if (k> n - k): 
         k = n - k 
  
     # Calculate value of [n*(n-1)*---*(n-k+1)] /
     # [k*(k-1)*---*1] 
     for i in range (k): 
      
         res * = (n - i) 
         res //= (i + 1 ) 
      
     return res 
  
# A Binomial coefficient based function to 
# find nth catalan number in O(n) time 
def catalan(n):
  
     # Calculate value of 2nCn 
     c = binomialCoeff( 2 * n, n) 
  
     # return 2nCn/(n+1) 
     return c //(n + 1 ) 
  
# A function to count number of BST 
# with n nodes using catalan 
def countBST(n):
  
     # find nth catalan number 
     count = catalan(n) 
  
     # return nth catalan number 
     return count 
  
# A function to count number of binary 
# trees with n nodes 
def countBT(n):
  
     # find count of BST with n numbers 
     count = catalan(n) 
  
     # return count * n! 
     return count * factorial(n) 
  
# Driver Code 
if __name__ = = '__main__' :
  
     n = 5
  
     # find count of BST and binary
     # trees with n nodes 
     count1 = countBST(n) 
     count2 = countBT(n) 
  
     # print count of BST and binary trees with n nodes 
     print ( "Count of BST with" , n, "nodes is" , count1) 
     print ( "Count of binary trees with" , n, "nodes is" , count2)
  
# This code is contributed by
# Shubham Singh(SHUBHAMSINGH10)

C#

//See https://www.lsbin.org/program-nth-catalan-number/
//for reference of below code.
using System;
  
class GFG
{
      
//A function to find 
//factorial of a given number
static int factorial( int n)
{
     int res = 1;
  
     //Calculate value of 
     //[1*(2)*---*(n-k+1)] /
     //[k*(k-1)*---*1]
     for ( int i = 1; i <= n; ++i)
     {
         res *= i;
     }
  
     return res;
}
  
static int binomialCoeff( int n, int k)
{
     int res = 1;
  
     //Since C(n, k) = C(n, n-k)
     if (k> n - k)
         k = n - k;
  
     //Calculate value of 
     //[n*(n-1)*---*(n-k+1)] /
     //[k*(k-1)*---*1]
     for ( int i = 0; i <k; ++i)
     {
         res *= (n - i);
         res /= (i + 1);
     }
  
     return res;
}
  
//A Binomial coefficient 
//based function to find 
//nth catalan number in 
//O(n) time
static int catalan( int n)
{
      
     //Calculate value
     //of 2nCn
     int c = binomialCoeff(2 * n, n);
  
     //return 2nCn/(n+1)
     return c /(n + 1);
}
  
//A function to count 
//number of BST with 
//n nodes using catalan
static int countBST( int n)
{
     //find nth catalan number
     int count = catalan(n);
  
     //return nth catalan number
     return count;
}
  
//A function to count number
//of binary trees with n nodes 
static int countBT( int n)
{
     //find count of BST
     //with n numbers
     int count = catalan(n);
  
     //return count * n!
     return count * factorial(n);
}
  
//Driver Code
static public void Main ()
{
     int count1, count2, n = 5;
      
     //find count of BST  
     //and binary trees 
     //with n nodes
     count1 = countBST(n);
     count2 = countBT(n); 
      
     //print count of BST and 
     //binary trees with n nodes
     Console.WriteLine( "Count of BST with " + 
                            n + " nodes is " + 
                                    count1);
     Console.WriteLine( "Count of binary " + 
                             "trees with " + 
                         n + " nodes is " + 
                                    count2);
     }
}
  
//This code is contributed
//by akt_mit

PHP

<?php
//See https://www.lsbin.org/program-nth-catalan-number/
//for reference of below code.
//A function to find factorial
//of a given number
function factorial( $n )
{
     $res = 1;
  
     //Calculate value of
     //[1*(2)*---*(n-k+1)] /
     //[k*(k-1)*---*1]
     for ( $i = 1; $i <= $n ; ++ $i )
     {
         $res *= $i ;
     }
  
     return $res ;
}
  
function binomialCoeff( $n , $k )
{
     $res = 1;
  
     //Since C(n, k) = C(n, n-k)
     if ( $k> $n - $k )
         $k = $n - $k ;
  
     //Calculate value of 
     //[n*(n-1)*---*(n-k+1)] /
     //[k*(k-1)*---*1]
     for ( $i = 0; $i <$k ; ++ $i )
     {
         $res *= ( $n - $i );
         $res = (int) $res /( $i + 1);
     }
  
     return $res ;
}
  
//A Binomial coefficient 
//based function to find 
//nth catalan number in
//O(n) time
function catalan( $n )
{
     //Calculate value of 2nCn
     $c = binomialCoeff(2 * $n , $n );
  
     //return 2nCn/(n+1)
     return (int) $c /( $n + 1);
}
  
//A function to count
//number of BST with 
//n nodes using catalan
function countBST( $n )
{
     //find nth catalan number
     $count = catalan( $n );
  
     //return nth 
     //catalan number
     return $count ;
}
  
//A function to count 
//number of binary 
//trees with n nodes 
function countBT( $n )
{
     //find count of 
     //BST with n numbers
     $count = catalan( $n );
  
     //return count * n!
     return $count * 
            factorial( $n );
}
  
//Driver Code
$count1 ;
$count2 ;
$n = 5;
  
//find count of BST and 
//binary trees with n nodes
$count1 = countBST( $n );
$count2 = countBT( $n ); 
  
//print count of BST and 
//binary trees with n nodes
echo "Count of BST with " , $n , " nodes is " , $count1 , "\n" ;
       
echo "Count of binary trees with " , $n , " nodes is " , $count2 ;
  
//This code is contributed by ajit
?>

输出如下：

Count of BST with 5 nodes is 42
Count of binary trees with 5 nodes is 5040

枚举证明

考虑所有可能的二进制搜索树, 每个元素都位于根目录。如果有n个节点, 则对于每个根节点选择, 都会有n – 1个非根节点, 并且这些非根节点必须划分为小于选定根的节点和大于选定根的节点。 。

假设节点i被选为根。然后是i –比i小1个节点和n –比i大的i节点。对于这两组节点中的每一个, 都有一定数量的可能子树。

令t(n)为具有n个节点的BST总数。以i为根的BST总数为t(i – 1)t(n – i)。由于左和右子树中的排列是独立的, 所以这两个项相乘在一起。也就是说, 对于左树中的每个排列和右树中的每个排列, 你将获得一个以i为根的BST。

对i求和得出具有n个节点的二叉搜索树的总数。

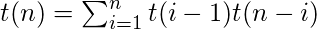
t（n）= \ sum_ {i = 1} ^ {n} t（i-1）t（n-i）

基本情况是t(0)= 1和t(1)= 1, 即有一个空的BST, 有一个BST和一个节点。

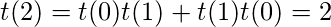
t（2）= t（0）t（1）+ t（1）t（0）= 2
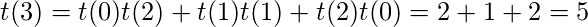
t（3）= t（0）t（2）+ t（1）t（1）+ t（2）t（0）= 2 + 1 + 2 = 5
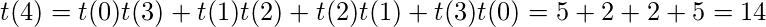
t（4）= t（0）t（3）+ t（1）t（2）+ t（2）t（1）+ t（3）t（0）= 5 + 2 + 2 + 5 = 14

同样, 关系countBT(n)= countBST(n)* n!持有。至于每个可能的BST, 都可以有n!二叉树, 其中n是BST中的节点数。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: