高级算法：跳转指针算法原理介绍和实现

本文概述

• C ++
• Python3

跳转指针算法是一种针对并行算法的设计技术, 该算法对指针结构(例如数组或链表)进行操作。此算法通常用于确定有根树的森林的根。

在跳转指针算法中, 我们对一棵树进行预处理, 以便人们可以回答查询以找到树中任何节点的任何父节点, 时间复杂度为O(log n).

跳转指针算法将最多log2n个指针关联到树的每个顶点。这些指针被称为跳转指针，因为它们向上跳转到树的根节点。对于处理树的任意节点，算法存储一个长度为l的跳数数组，其中l = log2(depth(v))。这个数组的第i个元素指向节点v的第2个父节点。这个数据结构帮助我们从任何给定的节点跳到树的一半。当要求算法处理查找树中任何节点的父节点的查询时，我们使用这些指针重复地向上跳转树。跳转的次数最多为log n，因此任何查找树中任何节点的父节点的问题都可以在O(log n)时间复杂度内得到回答。

在跳转指针中, 有一个从节点N到N的第j个父节点的指针,

j = 1, 2, 4, 8, …, 依此类推。所以我们存储每个节点的第2^(ith)个父节点。

跳转指针算法基本上适用于以下方法动态编程, 我们使用预先计算的结果来查找下一个结果。通过执行一些简单的计算, 我们可以计算出任何节点的数学公式k, 2Ĵk的父级等于21一2的父母1一k的父级.

该公式的简要说明在下面的算法部分中给出。

该算法最常见的用途是解决需要查找O(log n)时间复杂度的任何节点的祖先的查询。

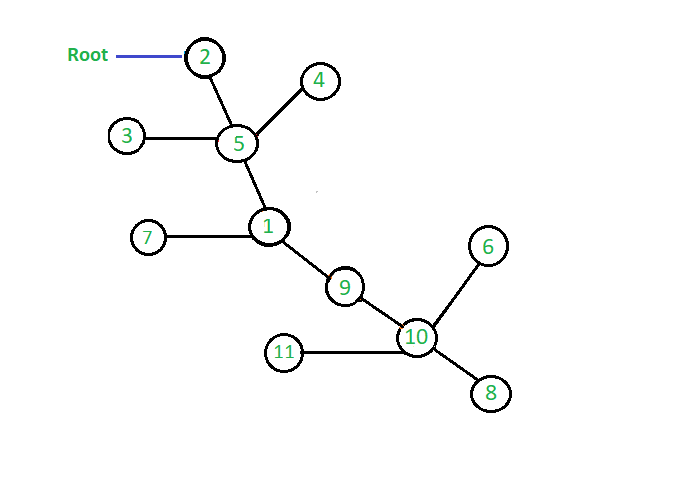
图来实现跳转指针算法：

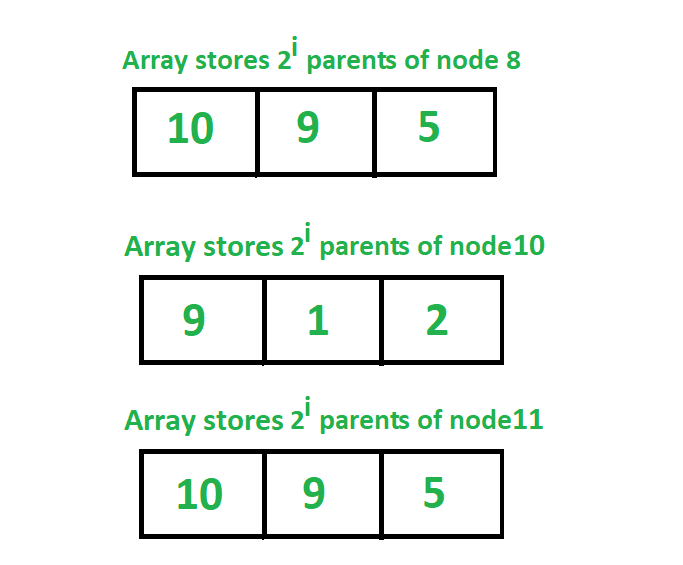
存储所有节点的第2个第i个父节点的跳转数组的表示形式：

例子：

Input: 0th parent of node 2 
Output: 0th parent of node 2 is = 2

Input: 2th parent of node 4
Output: 2th parent of node 4 is = 2

Input: 3rd parent of node 8 
Output: 3rd parent of node 8 is = 1

算法:

下面是实现跳转指针算法的算法，以查找图中任何节点的任何父节点。我们用动态规划的方法确定了跳跃矩阵。这里，我们表示根节点为R，并首先假设根节点的父节点为0，这意味着这个节点没有父节点。现在看看图和上面图中显示的数组，我们可以很容易地理解上面的公式来确定每个节点的第2个父节点。如果我们看看8节点值我们可以看到2^0父节点是10,现在找到2^1父节点我们看到2^1父2^0父节点的值是10和2^0的父节点10是8这意味着2^1的父节点2^0 2^0父节点的父节点8 8。同样，我们也可以看到节点8的第22个父节点是5，这是节点8的第2^1个父节点的第21个父节点，即节点的第2^1个父节点，值为9。

因此，通过这种方式，我们可以计算所有存储第2^i个父节点的跳转指针数组。

下面是伪代码, 用于计算存储2的跳转指针矩阵一世树中所有节点的父级。

jump[k][j] =   it points 2^jth parent of k    
             =  2^j-1th parent of (2^j-1th parent of k)       
             =  jump[jump[i][j-1][j-1]

实现:以下是实现上述算法的代码, 以查找O(logn)时间复杂度的任何节点的任何父节点。

C ++

//C++ program to implement Jump pointer algorithm
#include <bits/stdc++.h>
using namespace std;
 
int R = 0;
//n -> it represent total number of nodes
//len -> it is the maximum length of array
//to hold parent of each node.
//In worst case, the highest value of
//parent a node can have is n-1.
//2 ^ len <= n-1
//len = O(log2n)
int getLen( int n)
{
     int len = ( int )( log (n) /log (2)) + 1;
     return len;
}
 
//jump represent 2D matrix to hold parent of node in jump matrix
//here we pass reference of 2D matrix so that the change made
//occur directly to the original matrix
//len is same as defined above
//n is total nodes in graph
void set_jump_pointer(vector<vector<int>>& jump, int * node, int len, int n)
{
     for ( int j = 1; j <= len; j++)
         for ( int i = 0; i <n; i++)
             jump[node[i]][j] = jump[jump[node[i]][j - 1]][j - 1];
}
 
//c -> it represent child
//p -> it represent parent
//i -> it represent node number
//p=0 means the node is root node
//here also we pass reference of 2D matrix
//and depth vector so that the change made
//occur directly to the original matrix and original vector
void constructGraph(vector<vector<int>>& jump, int * node, int * isNode, int c, int p, int i)
{
     //enter the node in node array
     //it stores all the nodes in the graph
     node[i] = c;
 
     //to confirm that no child node have 2 parents
     if (isNode == 0) {
         isNode = 1;
         //make parent of x as y
         jump[0] = p;
     }
     return ;
}
 
//function to jump to Lth parent of any node
void jumpPointer(vector<vector<int>>& jump, int * isNode, int x, int L)
{
     int j = 0, n = x, k = L;
 
     //to check if node is present in graph or not
     if (isNode[x] == 0) {
         cout <<"Node is not present in graph " <<endl;
         return ;
     }
 
     //in this loop we decrease the value of L by L/2 and
     //increment j by 1 after each iteration, and check for set bit
     //if we get set bit then we update x with jth parent of x
     //as L becomes less than or equal to zero means
     //we have jumped to Lth parent of node x
     while (L> 0) {
         //to check if last bit is 1 or not
         if (L & 1)
             x = jump[x][j];
 
         //use of shift operator to make
         //L = L/2 after every iteration
         L = L>> 1;
         j++;
     }
 
     cout <<k <<"th parent of node " <<n
                    <<" is = " <<x <<endl;
 
     return ;
}
 
//Driver code
int main()
{
     //n represent number of nodes
     int n = 11;
 
     //initialization of parent matrix
     //suppose max range of a node is up to 1000
     //if there are 1000 nodes than also
     //length of jump matrix will not exceed 10
     vector<vector<int>> jump(1000, vector<int>(10));
 
     //node array is used to store all nodes
     int * node = new int [1000];
 
     //isNode is an array to check whether
     //a node is present in graph or not
     int * isNode = new int [1000];
 
     //memset function to initialize isNode array with 0
     memset (isNode, 0, 1000 * sizeof ( int ));
 
     //function to calculate len
     //len -> it is the maximum length of
     //array to hold parent of each node.
     int len = getLen(n);
 
     //R stores root node
     R = 2;
 
     //construction of graph
     //here 0 represent that the node is root node
     constructGraph(jump, node, isNode, 2, 0, 0);
     constructGraph(jump, node, isNode, 5, 2, 1);
     constructGraph(jump, node, isNode, 3, 5, 2);
     constructGraph(jump, node, isNode, 4, 5, 3);
     constructGraph(jump, node, isNode, 1, 5, 4);
     constructGraph(jump, node, isNode, 7, 1, 5);
     constructGraph(jump, node, isNode, 9, 1, 6);
     constructGraph(jump, node, isNode, 10, 9, 7);
     constructGraph(jump, node, isNode, 11, 10, 8);
     constructGraph(jump, node, isNode, 6, 10, 9);
     constructGraph(jump, node, isNode, 8, 10, 10);
 
     //function to pre compute jump matrix
     set_jump_pointer(jump, node, len, n);
 
     //query to jump to parent using jump pointers
     //query to jump to 1st parent of node 2
     jumpPointer(jump, isNode, 2, 0);
 
     //query to jump to 2nd parent of node 4
     jumpPointer(jump, isNode, 4, 2);
 
     //query to jump to 3rd parent of node 8
     jumpPointer(jump, isNode, 8, 3);
 
     //query to jump to 5th parent of node 20
     jumpPointer(jump, isNode, 20, 5);
 
     return 0;
}

Python3

# Python3 program to implement
# Jump pointer algorithm
import math
 
# Initialization of parent matrix
# suppose max range of a node is
# up to 1000 if there are 1000 nodes
#  than also length of jump matrix
# will not exceed 10
jump = [[ 0 for j in range ( 10 )]
            for i in range ( 1000 )]
  
# Node array is used to store all nodes
node = [ 0 for i in range ( 1000 )]
  
# isNode is an array to check whether
# a node is present in graph or not
isNode = [ 0 for i in range ( 1000 )]
 
# n -> it represent total number of nodes
# len -> it is the maximum length of array
# to hold parent of each node.
# In worst case, the highest value of
# parent a node can have is n-1.
# 2 ^ len <= n-1
# len = O(log2n)
def getLen(n):
 
     len = int ((math.log(n)) //
               (math.log( 2 ))) + 1
     return len
 
# jump represent 2D matrix to hold parent
# of node in jump matrix here we pass
# reference of 2D matrix so that the
# change made occur directly to the
# original matrix len is same as
# defined above n is total nodes
# in graph
def set_jump_pointer( len , n):
     
     global jump, node
     for j in range ( 1 , len + 1 ):
         for i in range ( 0 , n):
             jump[node[i]][j] = jump[jump[node[i]][j - 1 ]][j - 1 ]
 
# c -> it represent child
# p -> it represent parent
# i -> it represent node number
# p=0 means the node is root node
# here also we pass reference of
# 2D matrix and depth vector so
# that the change made occur
# directly to the original matrix
# and original vector
def constructGraph(c, p, i):
     
     global jump, node, isNode
     
     # Enter the node in node array
     # it stores all the nodes in the graph
     node[i] = c
  
     # To confirm that no child node
     # have 2 parents
     if (isNode = = 0 ):
         isNode = 1
         
         # Make parent of x as y
         jump[ 0 ] = p
     
     return
 
# function to jump to Lth parent
# of any node
def jumpPointer(x, L):
     
     j = 0
     n = x
     k = L
     
     global jump, isNode
     
     # To check if node is present in
     # graph or not
     if (isNode[x] = = 0 ):
         print ( "Node is not present in graph " )
         return
         
     # In this loop we decrease the value
     # of L by L/2 and increment j by 1
     # after each iteration, and check
     # for set bit if we get set bit
     # then we update x with jth parent
     # of x as L becomes less than or
     # equal to zero means we have
     # jumped to Lth parent of node x
     while (L> 0 ):
         
         # To check if last bit is 1 or not
         if ((L & 1 )! = 0 ):
             x = jump[x][j]
  
         # Use of shift operator to make
         # L = L/2 after every iteration
         L = L>> 1
         j + = 1
         
     print ( str (k) + "th parent of node " +
           str (n) + " is = " + str (x))  
  
     return
 
# Driver code
if __name__ = = "__main__" :
     
     # n represent number of nodes
     n = 11
  
     # Function to calculate len
     # len -> it is the maximum length of
     # array to hold parent of each node.
     len = getLen(n)
  
     # R stores root node
     R = 2
  
     # Construction of graph
     # here 0 represent that
     # the node is root node
     constructGraph( 2 , 0 , 0 )
     constructGraph( 5 , 2 , 1 )
     constructGraph( 3 , 5 , 2 )
     constructGraph( 4 , 5 , 3 )
     constructGraph( 1 , 5 , 4 )
     constructGraph( 7 , 1 , 5 )
     constructGraph( 9 , 1 , 6 )
     constructGraph( 10 , 9 , 7 )
     constructGraph( 11 , 10 , 8 )
     constructGraph( 6 , 10 , 9 )
     constructGraph( 8 , 10 , 10 )
  
     # Function to pre compute jump matrix
     set_jump_pointer( len , n)
  
     # Query to jump to parent using jump pointers
     # query to jump to 1st parent of node 2
     jumpPointer( 2 , 0 )
  
     # Query to jump to 2nd parent of node 4
     jumpPointer( 4 , 2 )
  
     # Query to jump to 3rd parent of node 8
     jumpPointer( 8 , 3 )
  
     # Query to jump to 5th parent of node 20
     jumpPointer( 20 , 5 )
 
# This code is contributed by rutvik_56

输出如下：

0th parent of node 2 is = 2
2th parent of node 4 is = 2
3th parent of node 8 is = 1
Node is not present in graph

---