高级数据结构：二项堆实现原理详细介绍

主要应用二进制堆作为工具优先级队列。二项堆是二进制堆提供更快的合并或合并操作以及Binary Heap提供的其他操作。

二项堆是二项树的集合

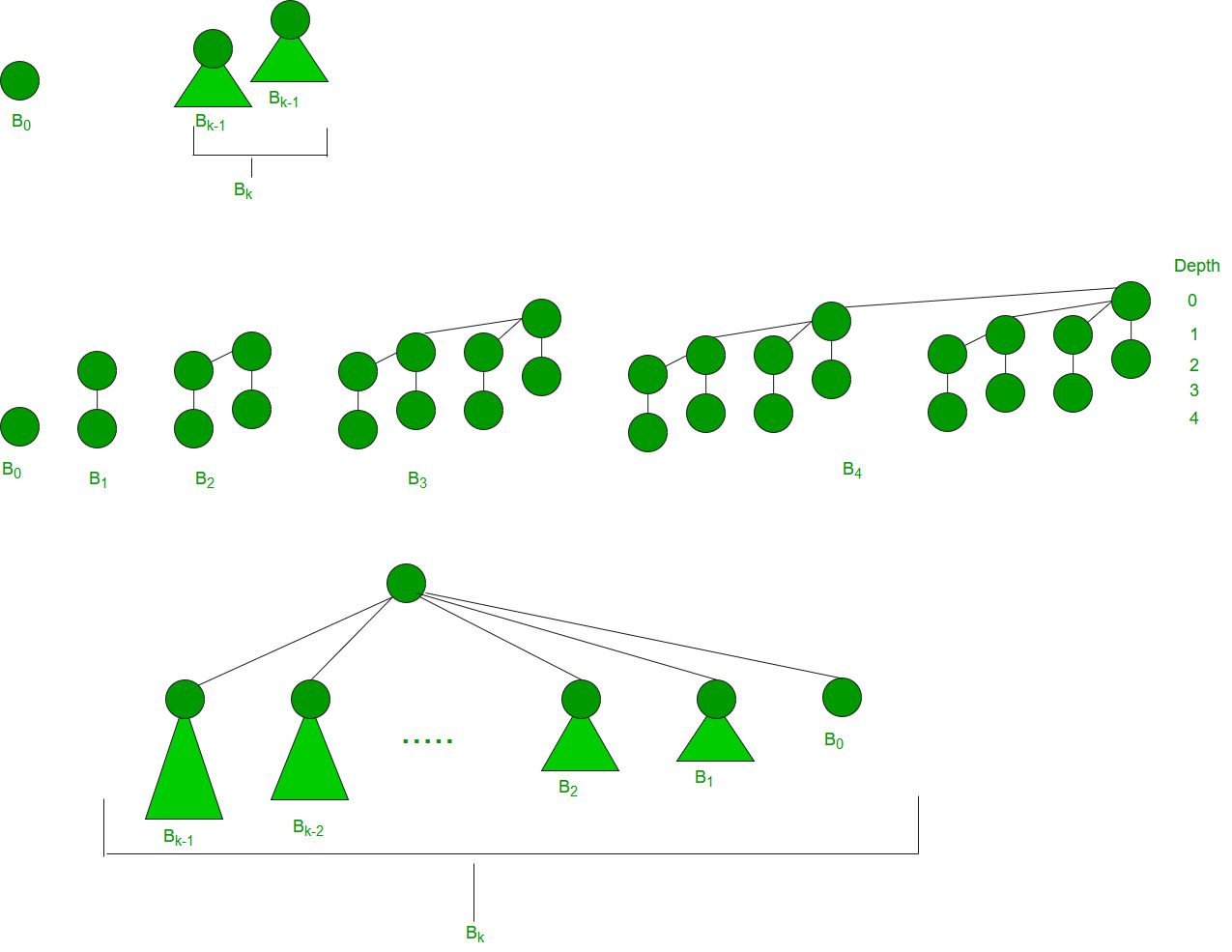
什么是二叉树？

顺序为0的二叉树有1个节点。可以通过取两个k-1阶二项树并将一个作为最左子项或另一个来构造k阶二项树。

k阶二叉树具有以下属性。

a)恰好有2^k个节点

b)深度为k。

c)当i = 0,1,...,k时，在深度i处恰好有kCi节点。

d)根的度数为k, 根的子代本身是二项树, 从左到右依次为k-1, k-2, .. 0。

k = 0 (Single Node)

 o

k = 1 (2 nodes) 
[We take two k = 0 order Binomial Trees, and
make one as child of other]
 o
   \
     o

k = 2 (4 nodes)
[We take two k = 1 order Binomial Trees, and
make one as child of other]
   o
 /\
o     o
       \
        o

k = 3 (8 nodes)
[We take two k = 2 order Binomial Trees, and
make one as child of other]
    o   
 /|  \ 
o   o    o
    |   /\
    o  o    o
             \
              o

下图是从第二版参考CLRS书.

二项堆：

二项堆是一组二项树, 其中每个二项树都遵循"最小堆"属性。最多可以有一个任何程度的二叉树。

二项堆示例：

12------------10--------------------20
             /\                 /| \
           15    50             70  50  40
           |                  /|    |     
           30               80  85  65 
                            |
                           100
A Binomial Heap with 13 nodes. It is a collection of 3 
Binomial Trees of orders 0, 2 and 3 from left to right. 

    10--------------------20
   /\                 /| \
 15    50             70  50  40
 |                  /|    |     
 30               80  85  65 
                  |
                 100

具有12个节点的二项堆。它是2的集合

从左到右顺序为2和3的二叉树。

数字和二项堆的二进制表示

具有n个节点的二项堆的二叉树的数量等于n的二进制表示形式中的设置位的数量。例如, 假设n为13, 则在n的二进制表示中有3个设置位(00001101), 因此有3个二叉树。我们还可以将这些二叉树的程度与设置位的位置相关联。通过这种关系, 我们可以得出结论, 在具有" n"个节点的二项堆中有O(Logn)个二叉树。

二项堆的操作：

二项堆中的主要操作是union(), 所有其他操作主要使用此操作。 union()操作是将两个二项堆合并为一个。让我们首先讨论其他操作, 稍后再讨论联合。

1)insert(H, k)：将键" k"插入二项堆" H"。此操作首先使用单键" k"创建一个二项堆, 然后在H和新的二项堆上调用并集。

2)getMin(H)：一种简单的getMin()方法是遍历二叉树的根列表并返回最小键。此实现需要O(Logn)时间。通过维护指向最小密钥根的指针, 可以将其优化为O(1)。

3)extractMin(H)：此操作还使用union()。我们首先调用getMin()来找到最小键二项树, 然后删除该节点并通过连接删除的最小节点的所有子树来创建新的二项堆。最后, 我们在H和新创建的二项堆上调用union()。此操作需要O(Logn)时间。

4)delete(H)：与Binary Heap一样, delete操作首先将键减小为负无穷大, 然后调用extractMin()。

5)reductionKey(H)：reductionKey()也类似于Binary Heap。我们将减少键与它的父键进行比较, 如果父键的键更多, 则交换键并为父键重复。当到达父级键较小的节点或击中根节点时, 我们将停止。 reductionKey()的时间复杂度为O(Logn)。

二项堆中的联合操作：

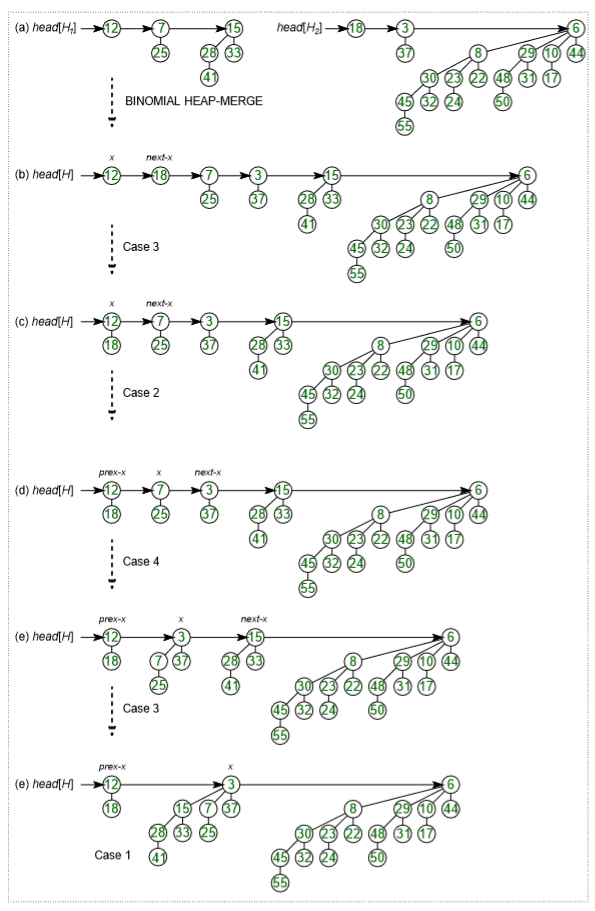
给定两个二项堆H1和H2, union(H1, H2)创建一个单个二项堆。

1)第一步是简单地以非降序合并两个堆。在下图中, 图(b)显示了合并后的结果。

2)简单合并后, 我们需要确保最多有一个任意顺序的二叉树。为此, 我们需要组合相同顺序的二叉树。我们遍历合并根的列表, 我们跟踪三个指针, prev, x和next-x。当遍历根目录列表时, 可能有以下4种情况。

---情况1：x和next-x的顺序不相同, 我们只是继续前进。

在以下3种情况下, x和next-x的顺序相同。

---情况2：如果next-next-x的顺序也相同, 请继续。

---情况3：如果x的键小于或等于next-x的键, 则通过将其与x链接, 使next-x成为x的子代。

---情况4：如果x的键更大, 则使x成为next的子代。

如何表示二项堆？

二项堆是一组二叉树。二叉树必须以允许从最左边的同级开始顺序访问所有同级的方式表示(我们需要in和extractMin()和delete())。想法是将二项树表示为最左侧的子级和右侧同级表示, 即每个节点存储两个指针, 一个指向最左侧的子级, 另一个指向右侧的同级。

二项堆的实现

资料来源：

Clifford Stein, Thomas H.Cormen, Charles E.Leiserson, Ronald L.

本文作者：湿婆。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。