本文概述
什么是最小生成树?
给定一个连通无向图,该图的生成树是一个子图,该子图是一棵连接所有顶点的树。一个图可以有许多不同的生成树。加权连通无向图的最小生成树(MST)或最小权生成树是权值小于或等于其他每棵生成树的权值的一棵生成树。一棵生成树的权值是它的每条边的权值之和。
一个最小生成树有多少条边?
最小生成树具有(V – 1)个边, 其中V是给定图中的顶点数。
最小生成树有哪些应用?
请参阅本文了解MST的应用。
以下是使用Kruskal算法查找MST的步骤
1.按重量的递减顺序对所有边进行排序。
2.选择最小的边。检查它是否与形成的生成树形成一个循环。如果未形成循环, 则包括该边。否则, 将其丢弃。
3.重复步骤2, 直到生成树中有(V-1)个边。
步骤2使用并集查找算法检测周期。因此,我们建议阅读以下文章作为先决条件。
联合查找算法|S1(图形中的检测周期)
联合查找算法|S2(按等级和路径压缩合并)
该算法是贪婪算法。贪婪的选择是选择迄今为止不会造成MST循环的最小重量边。让我们以一个示例来理解它:考虑以下输入图。
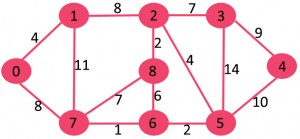
该图包含9个顶点和14个边。因此, 形成的最小生成树将具有(9 – 1)= 8个边。
After sorting:
Weight Src Dest
1 7 6
2 8 2
2 6 5
4 0 1
4 2 5
6 8 6
7 2 3
7 7 8
8 0 7
8 1 2
9 3 4
10 5 4
11 1 7
14 3 5现在从边排序列表中一一挑选所有边
1.挑边7-6:没有形成循环,包括它。

2.挑边8-2:没有形成循环,包括它。
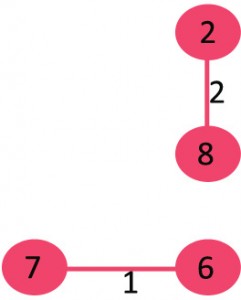
3.挑边6-5:没有形成循环,包括它。
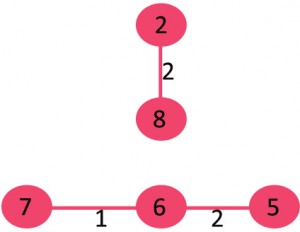
4.挑边0-1:没有形成循环,包括它。
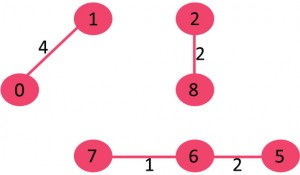
5.挑边2-5:没有形成循环,包括它。
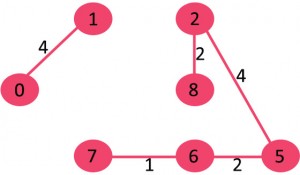
6.选择边8-6:因为包含这条边会导致循环,丢弃它。
7.挑边2-3:没有形成循环,包括它。
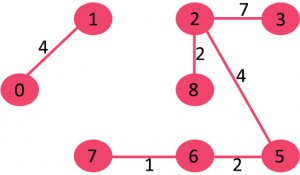
8.选择边7-8:因为包含这条边会导致循环,丢弃它。
9.选择边0-7:没有周期形成, 包括它。
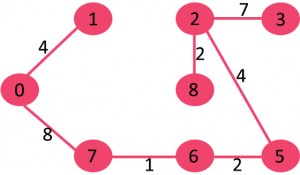
10.挑边1-2:由于包含此边沿会导致循环, 因此将其丢弃。
11.选边3-4:没有周期形成, 包括它。
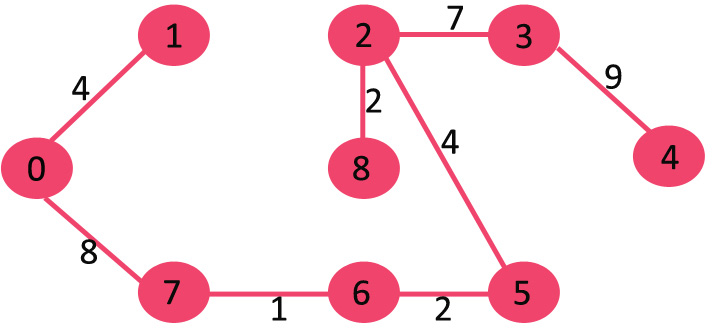
由于包含的边数等于(V – 1), 因此算法在此处停止。
以下是上述想法的实现:
C++
//C++ program for Kruskal's algorithm
// to find Minimum Spanning Tree of a
// given connected, undirected and weighted
// graph
#include <bits/stdc++.h>
using namespace std;
//a structure to represent a
//weighted edge in graph
class Edge {
public :
int src, dest, weight;
};
//a structure to represent a connected, //undirected and weighted graph
class Graph {
public :
//V-> Number of vertices, E-> Number of edges
int V, E;
//graph is represented as an array of edges.
//Since the graph is undirected, the edge
//from src to dest is also edge from dest
//to src. Both are counted as 1 edge here.
Edge* edge;
};
//Creates a graph with V vertices and E edges
Graph* createGraph( int V, int E)
{
Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
//A structure to represent a subset for union-find
class subset {
public :
int parent;
int rank;
};
//A utility function to find set of an element i
//(uses path compression technique)
int find(subset subsets[], int i)
{
//find root and make root as parent of i
//(path compression)
if (subsets[i].parent != i)
subsets[i].parent
= find(subsets, subsets[i].parent);
return subsets[i].parent;
}
//A function that does union of two sets of x and y
//(uses union by rank)
void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
//Attach smaller rank tree under root of high
//rank tree (Union by Rank)
if (subsets[xroot].rank <subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank> subsets[yroot].rank)
subsets[yroot].parent = xroot;
//If ranks are same, then make one as root and
//increment its rank by one
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
//Compare two edges according to their weights.
//Used in qsort() for sorting an array of edges
int myComp( const void * a, const void * b)
{
Edge* a1 = (Edge*)a;
Edge* b1 = (Edge*)b;
return a1->weight> b1->weight;
}
//The main function to construct MST using Kruskal's
//algorithm
void KruskalMST(Graph* graph)
{
int V = graph->V;
Edge result[V]; //Tnis will store the resultant MST
int e = 0; //An index variable, used for result[]
int i = 0; //An index variable, used for sorted edges
//Step 1: Sort all the edges in non-decreasing
//order of their weight. If we are not allowed to
//change the given graph, we can create a copy of
//array of edges
qsort (graph->edge, graph->E, sizeof (graph->edge[0]), myComp);
//Allocate memory for creating V ssubsets
subset* subsets = new subset[(V * sizeof (subset))];
//Create V subsets with single elements
for ( int v = 0; v <V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0;
}
//Number of edges to be taken is equal to V-1
while (e <V - 1 && i <graph->E)
{
//Step 2: Pick the smallest edge. And increment
//the index for next iteration
Edge next_edge = graph->edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
//If including this edge does't cause cycle, //include it in result and increment the index
//of result for next edge
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
//Else discard the next_edge
}
//print the contents of result[] to display the
//built MST
cout <<"Following are the edges in the constructed "
"MST\n" ;
int minimumCost = 0;
for (i = 0; i <e; ++i)
{
cout <<result[i].src <<" -- " <<result[i].dest
<<" == " <<result[i].weight <<endl;
minimumCost = minimumCost + result[i].weight;
}
//return;
cout <<"Minimum Cost Spanning Tree: " <<minimumCost
<<endl;
}
//Driver code
int main()
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; //Number of vertices in graph
int E = 5; //Number of edges in graph
Graph* graph = createGraph(V, E);
//add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
//add edge 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
//add edge 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
//add edge 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
//add edge 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
//Function call
KruskalMST(graph);
return 0;
}
//This code is contributed by rathbhupendraC
//C program for Kruskal's algorithm to find Minimum
//Spanning Tree of a given connected, undirected and
//weighted graph
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//a structure to represent a weighted edge in graph
struct Edge {
int src, dest, weight;
};
//a structure to represent a connected, undirected
//and weighted graph
struct Graph {
//V-> Number of vertices, E-> Number of edges
int V, E;
//graph is represented as an array of edges.
//Since the graph is undirected, the edge
//from src to dest is also edge from dest
//to src. Both are counted as 1 edge here.
struct Edge* edge;
};
//Creates a graph with V vertices and E edges
struct Graph* createGraph( int V, int E)
{
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
//A structure to represent a subset for union-find
struct subset {
int parent;
int rank;
};
//A utility function to find set of an element i
//(uses path compression technique)
int find( struct subset subsets[], int i)
{
//find root and make root as parent of i
//(path compression)
if (subsets[i].parent != i)
subsets[i].parent
= find(subsets, subsets[i].parent);
return subsets[i].parent;
}
//A function that does union of two sets of x and y
//(uses union by rank)
void Union( struct subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
//Attach smaller rank tree under root of high
//rank tree (Union by Rank)
if (subsets[xroot].rank <subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank> subsets[yroot].rank)
subsets[yroot].parent = xroot;
//If ranks are same, then make one as root and
//increment its rank by one
else
{
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
//Compare two edges according to their weights.
//Used in qsort() for sorting an array of edges
int myComp( const void * a, const void * b)
{
struct Edge* a1 = ( struct Edge*)a;
struct Edge* b1 = ( struct Edge*)b;
return a1->weight> b1->weight;
}
//The main function to construct MST using Kruskal's
//algorithm
void KruskalMST( struct Graph* graph)
{
int V = graph->V;
struct Edge
result[V]; //Tnis will store the resultant MST
int e = 0; //An index variable, used for result[]
int i = 0; //An index variable, used for sorted edges
//Step 1: Sort all the edges in non-decreasing
//order of their weight. If we are not allowed to
//change the given graph, we can create a copy of
//array of edges
qsort (graph->edge, graph->E, sizeof (graph->edge[0]), myComp);
//Allocate memory for creating V ssubsets
struct subset* subsets
= ( struct subset*) malloc (V * sizeof ( struct subset));
//Create V subsets with single elements
for ( int v = 0; v <V; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
//Number of edges to be taken is equal to V-1
while (e <V - 1 && i <graph->E) {
//Step 2: Pick the smallest edge. And increment
//the index for next iteration
struct Edge next_edge = graph->edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
//If including this edge does't cause cycle, //include it in result and increment the index
//of result for next edge
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
//Else discard the next_edge
}
//print the contents of result[] to display the
//built MST
printf (
"Following are the edges in the constructed MST\n" );
int minimumCost = 0;
for (i = 0; i <e; ++i)
{
printf ( "%d -- %d == %d\n" , result[i].src, result[i].dest, result[i].weight);
minimumCost += result[i].weight;
}
printf ( "Minimum Cost Spanning tree : %d" , minimumCost);
return ;
}
//Driver program to test above functions
int main()
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; //Number of vertices in graph
int E = 5; //Number of edges in graph
struct Graph* graph = createGraph(V, E);
//add edge 0-1
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = 10;
//add edge 0-2
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 6;
//add edge 0-3
graph->edge[2].src = 0;
graph->edge[2].dest = 3;
graph->edge[2].weight = 5;
//add edge 1-3
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 15;
//add edge 2-3
graph->edge[4].src = 2;
graph->edge[4].dest = 3;
graph->edge[4].weight = 4;
KruskalMST(graph);
return 0;
}Java
//Java program for Kruskal's algorithm to
//find Minimum Spanning Tree of a given
//connected, undirected and weighted graph
import java.util.*;
import java.lang.*;
import java.io.*;
class Graph {
//A class to represent a graph edge
class Edge implements Comparable<Edge>
{
int src, dest, weight;
//Comparator function used for
//sorting edgesbased on their weight
public int compareTo(Edge compareEdge)
{
return this .weight - compareEdge.weight;
}
};
//A class to represent a subset for
//union-find
class subset
{
int parent, rank;
};
int V, E; //V-> no. of vertices & E->no.of edges
Edge edge[]; //collection of all edges
//Creates a graph with V vertices and E edges
Graph( int v, int e)
{
V = v;
E = e;
edge = new Edge[E];
for ( int i = 0 ; i <e; ++i)
edge[i] = new Edge();
}
//A utility function to find set of an
//element i (uses path compression technique)
int find(subset subsets[], int i)
{
//find root and make root as parent of i
//(path compression)
if (subsets[i].parent != i)
subsets[i].parent
= find(subsets, subsets[i].parent);
return subsets[i].parent;
}
//A function that does union of two sets
//of x and y (uses union by rank)
void Union(subset subsets[], int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
//Attach smaller rank tree under root
//of high rank tree (Union by Rank)
if (subsets[xroot].rank
<subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank
> subsets[yroot].rank)
subsets[yroot].parent = xroot;
//If ranks are same, then make one as
//root and increment its rank by one
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
//The main function to construct MST using Kruskal's
//algorithm
void KruskalMST()
{
//Tnis will store the resultant MST
Edge result[] = new Edge[V];
//An index variable, used for result[]
int e = 0 ;
//An index variable, used for sorted edges
int i = 0 ;
for (i = 0 ; i <V; ++i)
result[i] = new Edge();
//Step 1: Sort all the edges in non-decreasing
//order of their weight. If we are not allowed to
//change the given graph, we can create a copy of
//array of edges
Arrays.sort(edge);
//Allocate memory for creating V ssubsets
subset subsets[] = new subset[V];
for (i = 0 ; i <V; ++i)
subsets[i] = new subset();
//Create V subsets with single elements
for ( int v = 0 ; v <V; ++v)
{
subsets[v].parent = v;
subsets[v].rank = 0 ;
}
i = 0 ; //Index used to pick next edge
//Number of edges to be taken is equal to V-1
while (e <V - 1 )
{
//Step 2: Pick the smallest edge. And increment
//the index for next iteration
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
//If including this edge does't cause cycle, //include it in result and increment the index
//of result for next edge
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
//Else discard the next_edge
}
//print the contents of result[] to display
//the built MST
System.out.println( "Following are the edges in "
+ "the constructed MST" );
int minimumCost = 0 ;
for (i = 0 ; i <e; ++i)
{
System.out.println(result[i].src + " -- "
+ result[i].dest
+ " == " + result[i].weight);
minimumCost += result[i].weight;
}
System.out.println( "Minimum Cost Spanning Tree "
+ minimumCost);
}
//Driver Code
public static void main(String[] args)
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4 ; //Number of vertices in graph
int E = 5 ; //Number of edges in graph
Graph graph = new Graph(V, E);
//add edge 0-1
graph.edge[ 0 ].src = 0 ;
graph.edge[ 0 ].dest = 1 ;
graph.edge[ 0 ].weight = 10 ;
//add edge 0-2
graph.edge[ 1 ].src = 0 ;
graph.edge[ 1 ].dest = 2 ;
graph.edge[ 1 ].weight = 6 ;
//add edge 0-3
graph.edge[ 2 ].src = 0 ;
graph.edge[ 2 ].dest = 3 ;
graph.edge[ 2 ].weight = 5 ;
//add edge 1-3
graph.edge[ 3 ].src = 1 ;
graph.edge[ 3 ].dest = 3 ;
graph.edge[ 3 ].weight = 15 ;
//add edge 2-3
graph.edge[ 4 ].src = 2 ;
graph.edge[ 4 ].dest = 3 ;
graph.edge[ 4 ].weight = 4 ;
//Function call
graph.KruskalMST();
}
}
//This code is contributed by Aakash Hasijapython
# Python program for Kruskal's algorithm to find
# Minimum Spanning Tree of a given connected, # undirected and weighted graph
from collections import defaultdict
# Class to represent a graph
class Graph:
def __init__( self , vertices):
self .V = vertices # No. of vertices
self .graph = [] # default dictionary
# to store graph
# function to add an edge to graph
def addEdge( self , u, v, w):
self .graph.append([u, v, w])
# A utility function to find set of an element i
# (uses path compression technique)
def find( self , parent, i):
if parent[i] = = i:
return i
return self .find(parent, parent[i])
# A function that does union of two sets of x and y
# (uses union by rank)
def union( self , parent, rank, x, y):
xroot = self .find(parent, x)
yroot = self .find(parent, y)
# Attach smaller rank tree under root of
# high rank tree (Union by Rank)
if rank[xroot] <rank[yroot]:
parent[xroot] = yroot
elif rank[xroot]> rank[yroot]:
parent[yroot] = xroot
# If ranks are same, then make one as root
# and increment its rank by one
else :
parent[yroot] = xroot
rank[xroot] + = 1
# The main function to construct MST using Kruskal's
# algorithm
def KruskalMST( self ):
result = [] # This will store the resultant MST
# An index variable, used for sorted edges
i = 0
# An index variable, used for result[]
e = 0
# Step 1: Sort all the edges in
# non-decreasing order of their
# weight. If we are not allowed to change the
# given graph, we can create a copy of graph
self .graph = sorted ( self .graph, key = lambda item: item[ 2 ])
parent = []
rank = []
# Create V subsets with single elements
for node in range ( self .V):
parent.append(node)
rank.append( 0 )
# Number of edges to be taken is equal to V-1
while e <self .V - 1 :
# Step 2: Pick the smallest edge and increment
# the index for next iteration
u, v, w = self .graph[i]
i = i + 1
x = self .find(parent, u)
y = self .find(parent, v)
# If including this edge does't
# cause cycle, include it in result
# and increment the indexof result
# for next edge
if x ! = y:
e = e + 1
result.append([u, v, w])
self .union(parent, rank, x, y)
# Else discard the edge
minimumCost = 0
print "Edges in the constructed MST"
for u, v, weight in result:
minimumCost + = weight
print ( "%d -- %d == %d" % (u, v, weight))
print ( "Minimum Spanning Tree" , minimumCost)
# Driver code
g = Graph( 4 )
g.addEdge( 0 , 1 , 10 )
g.addEdge( 0 , 2 , 6 )
g.addEdge( 0 , 3 , 5 )
g.addEdge( 1 , 3 , 15 )
g.addEdge( 2 , 3 , 4 )
# Function call
g.KruskalMST()
# This code is contributed by Neelam YadavC#
//C# Code for above approach
using System;
class Graph {
//A class to represent a graph edge
class Edge : IComparable<Edge> {
public int src, dest, weight;
//Comparator function used for sorting edges
//based on their weight
public int CompareTo(Edge compareEdge)
{
return this .weight
- compareEdge.weight;
}
}
//A class to represent
//a subset for union-find
public class subset
{
public int parent, rank;
};
int V, E; //V-> no. of vertices & E->no.of edges
Edge[] edge; //collection of all edges
//Creates a graph with V vertices and E edges
Graph( int v, int e)
{
V = v;
E = e;
edge = new Edge[E];
for ( int i = 0; i <e; ++i)
edge[i] = new Edge();
}
//A utility function to find set of an element i
//(uses path compression technique)
int find(subset[] subsets, int i)
{
//find root and make root as
//parent of i (path compression)
if (subsets[i].parent != i)
subsets[i].parent
= find(subsets, subsets[i].parent);
return subsets[i].parent;
}
//A function that does union of
//two sets of x and y (uses union by rank)
void Union(subset[] subsets, int x, int y)
{
int xroot = find(subsets, x);
int yroot = find(subsets, y);
//Attach smaller rank tree under root of
//high rank tree (Union by Rank)
if (subsets[xroot].rank <subsets[yroot].rank)
subsets[xroot].parent = yroot;
else if (subsets[xroot].rank> subsets[yroot].rank)
subsets[yroot].parent = xroot;
//If ranks are same, then make one as root
//and increment its rank by one
else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
//The main function to construct MST
//using Kruskal's algorithm
void KruskalMST()
{
//This will store the
//resultant MST
Edge[] result = new Edge[V];
int e = 0; //An index variable, used for result[]
int i
= 0; //An index variable, used for sorted edges
for (i = 0; i <V; ++i)
result[i] = new Edge();
//Step 1: Sort all the edges in non-decreasing
//order of their weight. If we are not allowed
//to change the given graph, we can create
//a copy of array of edges
Array.Sort(edge);
//Allocate memory for creating V ssubsets
subset[] subsets = new subset[V];
for (i = 0; i <V; ++i)
subsets[i] = new subset();
//Create V subsets with single elements
for ( int v = 0; v <V; ++v) {
subsets[v].parent = v;
subsets[v].rank = 0;
}
i = 0; //Index used to pick next edge
//Number of edges to be taken is equal to V-1
while (e <V - 1)
{
//Step 2: Pick the smallest edge. And increment
//the index for next iteration
Edge next_edge = new Edge();
next_edge = edge[i++];
int x = find(subsets, next_edge.src);
int y = find(subsets, next_edge.dest);
//If including this edge does't cause cycle, //include it in result and increment the index
//of result for next edge
if (x != y) {
result[e++] = next_edge;
Union(subsets, x, y);
}
//Else discard the next_edge
}
//print the contents of result[] to display
//the built MST
Console.WriteLine( "Following are the edges in "
+ "the constructed MST" );
int minimumCost = 0
for (i = 0; i <e; ++i)
{
Console.WriteLine(result[i].src + " -- "
+ result[i].dest
+ " == " + result[i].weight);
minimumCost += result[i].weight;
}
Console.WriteLine( "Minimum Cost Spanning Tree"
+ minimumCost);
Console.ReadLine();
}
//Driver Code
public static void Main(String[] args)
{
/* Let us create following weighted graph
10
0--------1
| \ |
6| 5\ |15
| \ |
2--------3
4 */
int V = 4; //Number of vertices in graph
int E = 5; //Number of edges in graph
Graph graph = new Graph(V, E);
//add edge 0-1
graph.edge[0].src = 0;
graph.edge[0].dest = 1;
graph.edge[0].weight = 10;
//add edge 0-2
graph.edge[1].src = 0;
graph.edge[1].dest = 2;
graph.edge[1].weight = 6;
//add edge 0-3
graph.edge[2].src = 0;
graph.edge[2].dest = 3;
graph.edge[2].weight = 5;
//add edge 1-3
graph.edge[3].src = 1;
graph.edge[3].dest = 3;
graph.edge[3].weight = 15;
//add edge 2-3
graph.edge[4].src = 2;
graph.edge[4].dest = 3;
graph.edge[4].weight = 4;
//Function call
graph.KruskalMST();
}
}
//This code is contributed by Aakash Hasija输出如下
Following are the edges in the constructed MST
2 -- 3 == 4
0 -- 3 == 5
0 -- 1 == 10
Minimum Cost Spanning Tree: 19时间复杂度:O(ElogE)或O(ElogV)。边排序需要O(ELogE)时间。排序后, 我们遍历所有边并应用find-union算法。查找和联合操作最多需要O(LogV)时间。因此, 总体复杂度为O(ELogE + ELogV)时间。 E的值最大为O(V2), 因此O(LogV)与O(LogE)相同。因此, 总体时间复杂度为O(ElogE)或O(ElogV)
参考文献:
http://www.ics.uci.edu/~eppstein/161/960206.html
http://en.wikipedia.org/wiki/Minimum_spanning_tree
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)