算法设计：在数组中找到对数(x, y)，使得x^y大于y^x

2021年4月6日19:41:14 发表评论 693 次浏览

本文概述

给定两个正整数数组X []和Y [], 找到对数, 使得x ^ y > y ^ x其中x是X []的元素, y是Y []的元素。

例子：

输入：X [] = {2, 1, 6}, Y = {1, 5}
输出：3
说明：总共有3对, 其中pow(x, y)大于pow(y, x)对是( 2, 1), (2、5)和(6, 1)
输入：X [] = {10, 19, 18}, Y [] = {11, 15, 9}
输出：2
说明：总共2对, 其中pow(x, y)大于pow(y, x)对是(10, 11)和(10, 15)

蛮力解决方案是考虑X []和Y []的每个元素, 并检查给定条件是否满足。

以下是基于蛮力解决方案的C ++代码。

Python3

def countPairsBruteForce(X, Y, m, n):
     ans = 0 
     for i in range (m):
         for j in range (n):
             if ( pow (X[i], Y[j]) > pow (Y[j], X[i])):
                 ans + = 1 
     return ans 
      
# This code is contributed by shubhamsingh10

C ++

int countPairsBruteForce( int X[], int Y[], int m, int n)
{
     int ans = 0;
     for ( int i = 0; i < m; i++)
        for ( int j = 0; j < n; j++)
           if ( pow (X[i], Y[j]) > pow (Y[j], X[i]))
               ans++;
     return ans;
}

时间复杂度：O(M * N)其中中号和ñ是给定数组的大小。

高效的解决方案：

这个问题可以解决

O(nLogn + mLogn)

时间。诀窍是, 如果

y> x

然后

x ^ y> y ^ x

除了一些例外。

以下是基于此技巧的简单步骤。

  • 排序数组Y []。
  • 对于X []中的每个x, 使用以下公式找到Y []中大于x的最小数字的索引idx(也称为x的ceil)二进制搜索或者我们可以使用内置功能upper_bound()在算法库中。
  • idx之后的所有数字都满足该关系, 因此只需将(n-idx)添加到计数中即可。

基本案例和例外：

以下是X []中的x和Y []中的y的例外

  • 如果x = 0, 则此x的对数为0。
  • 如果x = 1, 则此x的对数等于Y []中的0s数。
  • x小于y表示x ^ y大于y ^ x。
    1. x = 2, y = 3或4
    2. x = 3, y = 2

注意, 不存在x = 4和y = 2的情况

下图以表格形式显示了所有例外情况。值1表示对应的(x, y)形成有效对。

异常表

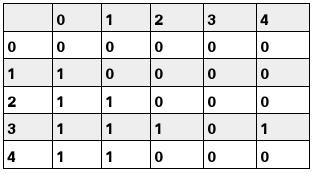
在下面的实现中, 我们对Y数组进行预处理, 并对其中的0、1、2、3和4进行计数, 以便我们可以在恒定时间内处理所有异常。数组NoOfY []用于存储计数。

下面是上述方法的实现：

C ++

// C++ program to finds the number of pairs (x, y)
// in an array such that x^y > y^x
  
#include<bits/stdc++.h>
using namespace std;
  
// Function to return count of pairs with x as one element
// of the pair. It mainly looks for all values in Y[] where
// x ^ Y[i] > Y[i] ^ x
int count( int x, int Y[], int n, int NoOfY[])
{
     // If x is 0, then there cannot be any value in Y such that
     // x^Y[i] > Y[i]^x
     if (x == 0) return 0;
  
     // If x is 1, then the number of pais is equal to number of
     // zeroes in Y[]
     if (x == 1) return NoOfY[0];
  
     // Find number of elements in Y[] with values greater than x
     // upper_bound() gets address of first greater element in Y[0..n-1]
     int * idx = upper_bound(Y, Y + n, x);
     int ans = (Y + n) - idx;
  
     // If we have reached here, then x must be greater than 1, // increase number of pairs for y=0 and y=1
     ans += (NoOfY[0] + NoOfY[1]);
  
     // Decrease number of pairs for x=2 and (y=4 or y=3)
     if (x == 2)  ans -= (NoOfY[3] + NoOfY[4]);
  
     // Increase number of pairs for x=3 and y=2
     if (x == 3)  ans += NoOfY[2];
  
     return ans;
}
  
// Function to return count of pairs (x, y) such that
// x belongs to X[], y belongs to Y[] and x^y > y^x
int countPairs( int X[], int Y[], int m, int n)
{
     // To store counts of 0, 1, 2, 3 and 4 in array Y
     int NoOfY[5] = {0};
     for ( int i = 0; i < n; i++)
         if (Y[i] < 5)
             NoOfY[Y[i]]++;
  
     // Sort Y[] so that we can do binary search in it
     sort(Y, Y + n);
  
     int total_pairs = 0; // Initialize result
  
     // Take every element of X and count pairs with it
     for ( int i=0; i<m; i++)
         total_pairs += count(X[i], Y, n, NoOfY);
  
     return total_pairs;
}
  
// Driver program 
int main()
{
     int X[] = {2, 1, 6};
     int Y[] = {1, 5};
  
     int m = sizeof (X)/ sizeof (X[0]);
     int n = sizeof (Y)/ sizeof (Y[0]);
  
     cout << "Total pairs = " << countPairs(X, Y, m, n);
  
     return 0;
}

Java

// Java program to finds number of pairs (x, y)
// in an array such that x^y > y^x
  
import java.util.Arrays;
  
class Test
{
     // Function to return count of pairs with x as one element
     // of the pair. It mainly looks for all values in Y[] where
     // x ^ Y[i] > Y[i] ^ x
     static int count( int x, int Y[], int n, int NoOfY[])
     {
         // If x is 0, then there cannot be any value in Y such that
         // x^Y[i] > Y[i]^x
         if (x == 0 ) return 0 ;
       
         // If x is 1, then the number of pais is equal to number of
         // zeroes in Y[]
         if (x == 1 ) return NoOfY[ 0 ];
       
         // Find number of elements in Y[] with values greater than x
         // getting upperbound of x with binary search
         int idx = Arrays.binarySearch(Y, x);
         int ans;
         if (idx < 0 ){
             idx = Math.abs(idx+ 1 );
             ans = Y.length - idx;
         }
         else {
             while (idx<n && Y[idx]==x) {
                 idx++;
             }
             ans = Y.length - idx;
         }
       
         // If we have reached here, then x must be greater than 1, // increase number of pairs for y=0 and y=1
         ans += (NoOfY[ 0 ] + NoOfY[ 1 ]);
       
         // Decrease number of pairs for x=2 and (y=4 or y=3)
         if (x == 2 )  ans -= (NoOfY[ 3 ] + NoOfY[ 4 ]);
       
         // Increase number of pairs for x=3 and y=2
         if (x == 3 )  ans += NoOfY[ 2 ];
       
         return ans;
     }
       
     // Function to returns count of pairs (x, y) such that
     // x belongs to X[], y belongs to Y[] and x^y > y^x
     static int countPairs( int X[], int Y[], int m, int n)
     {
         // To store counts of 0, 1, 2, 3 and 4 in array Y
         int NoOfY[] = new int [ 5 ];
         for ( int i = 0 ; i < n; i++)
             if (Y[i] < 5 )
                 NoOfY[Y[i]]++;
       
         // Sort Y[] so that we can do binary search in it
         Arrays.sort(Y);
       
         int total_pairs = 0 ; // Initialize result
       
         // Take every element of X and count pairs with it
         for ( int i= 0 ; i<m; i++)
             total_pairs += count(X[i], Y, n, NoOfY);
       
         return total_pairs;
     }
      
     // Driver method
     public static void main(String args[])
     {
         int X[] = { 2 , 1 , 6 };
         int Y[] = { 1 , 5 };
       
         System.out.println( "Total pairs = " + countPairs(X, Y, X.length, Y.length));
     }
}

Python3

# Python3 program to find the number 
# of pairs (x, y) in an array
# such that x^y > y^x 
import bisect
  
# Function to return count of pairs 
# with x as one element of the pair.
# It mainly looks for all values in Y 
# where x ^ Y[i] > Y[i] ^ x 
def count(x, Y, n, NoOfY):
      
     # If x is 0, then there cannot be 
     # any value in Y such that
     # x^Y[i] > Y[i]^x 
     if x = = 0 :
         return 0
  
     # If x is 1, then the number of pairs 
     # is equal to number of zeroes in Y
     if x = = 1 :
         return NoOfY[ 0 ]
  
     # Find number of elements in Y[] with 
     # values greater than x, bisect.bisect_right 
     # gets address of first greater element 
     # in Y[0..n-1]
     idx = bisect.bisect_right(Y, x)
     ans = n - idx
  
     # If we have reached here, then x must be greater than 1, # increase number of pairs for y=0 and y=1 
     ans + = NoOfY[ 0 ] + NoOfY[ 1 ]
  
     # Decrease number of pairs 
     # for x=2 and (y=4 or y=3)
     if x = = 2 :
         ans - = NoOfY[ 3 ] + NoOfY[ 4 ]
  
     # Increase number of pairs
     # for x=3 and y=2 
     if x = = 3 :
         ans + = NoOfY[ 2 ]
  
     return ans
  
# Function to return count of pairs (x, y) 
# such that x belongs to X, # y belongs to Y and x^y > y^x
def count_pairs(X, Y, m, n):
  
     # To store counts of 0, 1, 2, 3, # and 4 in array Y
     NoOfY = [ 0 ] * 5
     for i in range (n):
         if Y[i] < 5 :
             NoOfY[Y[i]] + = 1
              
     # Sort Y so that we can do binary search in it
     Y.sort()
     total_pairs = 0 # Initialize result
  
     # Take every element of X and 
     # count pairs with it 
     for x in X:
         total_pairs + = count(x, Y, n, NoOfY)
  
     return total_pairs
  
# Driver Code
if __name__ = = '__main__' :
  
     X = [ 2 , 1 , 6 ]
     Y = [ 1 , 5 ]
     print ( "Total pairs = " , count_pairs(X, Y, len (X), len (Y)))
  
# This code is contributed by shaswatd673

C#

// C# program to finds number of pairs (x, y)
// in an array such that x^y > y^x
using System;
  
class GFG {
      
     // Function to return count of pairs 
     // with x as one element of the pair.
     // It mainly looks for all values in Y[] 
     // where x ^ Y[i] > Y[i] ^ x
     static int count( int x, int [] Y, int n, int [] NoOfY)
     {
         // If x is 0, then there cannot be any 
         // value in Y such that x^Y[i] > Y[i]^x
         if (x == 0)
             return 0;
  
         // If x is 1, then the number of pais 
         // is equal to number of zeroes in Y[]
         if (x == 1)
             return NoOfY[0];
  
         // Find number of elements in Y[] with 
         // values greater than x getting 
         // upperbound of x with binary search
         int idx = Array.BinarySearch(Y, x);
         int ans;
         if (idx < 0) {
             idx = Math.Abs(idx + 1);
             ans = Y.Length - idx;
         }
          
         else {
             while (idx<n && Y[idx] == x) {
                 idx++;
             }
             ans = Y.Length - idx;
         }
  
         // If we have reached here, then x
         // must be greater than 1, increase 
         // number of pairs for y = 0 and y = 1
         ans += (NoOfY[0] + NoOfY[1]);
  
         // Decrease number of pairs 
         // for x = 2 and (y = 4 or y = 3)
         if (x == 2)
             ans -= (NoOfY[3] + NoOfY[4]);
  
         // Increase number of pairs for x = 3 and y = 2
         if (x == 3)
             ans += NoOfY[2];
  
         return ans;
     }
  
     // Function to that returns count
     // of pairs (x, y) such that x belongs 
     // to X[], y belongs to Y[] and x^y > y^x
     static int countPairs( int [] X, int [] Y, int m, int n)
     {
         // To store counts of 0, 1, 2, 3 and 4 in array Y
         int [] NoOfY = new int [5];
         for ( int i = 0; i < n; i++)
             if (Y[i] < 5)
                 NoOfY[Y[i]]++;
  
         // Sort Y[] so that we can do binary search in it
         Array.Sort(Y);
  
         int total_pairs = 0; // Initialize result
  
         // Take every element of X and count pairs with it
         for ( int i = 0; i < m; i++)
             total_pairs += count(X[i], Y, n, NoOfY);
  
         return total_pairs;
     }
  
     // Driver method
     public static void Main()
     {
         int [] X = { 2, 1, 6 };
         int [] Y = { 1, 5 };
  
         Console.Write( "Total pairs = " + 
                        countPairs(X, Y, X.Length, Y.Length));
     }
}
  
// This code is contributed by Sam007

输出如下：

Total pairs = 3

时间复杂度：O(nLogn + mLogn), 其中m和n分别是数组X []和Y []的大小。排序步骤需要O(nLogn)时间。然后, 使用二进制搜索在Y []中搜索X []的每个元素。此步骤需要O(mLogn)时间。

本文作者：Shubham Mittal。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: