本文概述
树的层次顺序遍历是树的广度优先遍历。
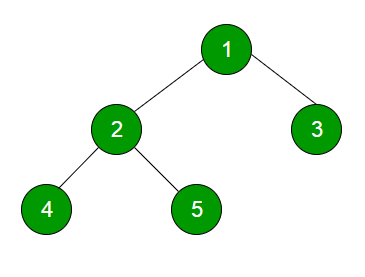
上面树的级别顺序遍历为1 2 3 4 5
方法1(使用函数打印给定级别)
算法:
此方法基本上有两个函数。一种是打印给定级别(printGivenLevel)的所有节点, 另一种是打印树的级别顺序遍历(printLevelorder)。 printLevelorder利用printGivenLevel从根开始一个接一个地打印所有级别的节点。
/*Function to print level order traversal of tree*/
printLevelorder(tree)
for d = 1 to height(tree)
printGivenLevel(tree, d);
/*Function to print all nodes at a given level*/
printGivenLevel(tree, level)
if tree is NULL then return;
if level is 1, then
print(tree->data);
else if level greater than 1, then
printGivenLevel(tree->left, level-1);
printGivenLevel(tree->right, level-1);实现
C ++
// Recursive CPP program for level
// order traversal of Binary Tree
#include <bits/stdc++.h>
using namespace std;
/* A binary tree node has data, pointer to left child
and a pointer to right child */
class node
{
public :
int data;
node* left, *right;
};
/* Function protoypes */
void printGivenLevel(node* root, int level);
int height(node* node);
node* newNode( int data);
/* Function to print level
order traversal a tree*/
void printLevelOrder(node* root)
{
int h = height(root);
int i;
for (i = 1; i <= h; i++)
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel(node* root, int level)
{
if (root == NULL)
return ;
if (level == 1)
cout << root->data << " " ;
else if (level > 1)
{
printGivenLevel(root->left, level-1);
printGivenLevel(root->right, level-1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(node* node)
{
if (node == NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return (lheight + 1);
else return (rheight + 1);
}
}
/* Helper function that allocates
a new node with the given data and
NULL left and right pointers. */
node* newNode( int data)
{
node* Node = new node();
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return (Node);
}
/* Driver code*/
int main()
{
node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n" ;
printLevelOrder(root);
return 0;
}
// This code is contributed by rathbhupendraC
// Recursive C program for level
// order traversal of Binary Tree
#include <stdio.h>
#include <stdlib.h>
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left, *right;
};
/* Function protoypes */
void printGivenLevel( struct node* root, int level);
int height( struct node* node);
struct node* newNode( int data);
/* Function to print level order traversal a tree*/
void printLevelOrder( struct node* root)
{
int h = height(root);
int i;
for (i=1; i<=h; i++)
printGivenLevel(root, i);
}
/* Print nodes at a given level */
void printGivenLevel( struct node* root, int level)
{
if (root == NULL)
return ;
if (level == 1)
printf ( "%d " , root->data);
else if (level > 1)
{
printGivenLevel(root->left, level-1);
printGivenLevel(root->right, level-1);
}
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height( struct node* node)
{
if (node==NULL)
return 0;
else
{
/* compute the height of each subtree */
int lheight = height(node->left);
int rheight = height(node->right);
/* use the larger one */
if (lheight > rheight)
return (lheight+1);
else return (rheight+1);
}
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode( int data)
{
struct node* node = ( struct node*)
malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf ( "Level Order traversal of binary tree is \n" );
printLevelOrder(root);
return 0;
}Java
// Recursive Java program for level
// order traversal of Binary Tree
/* Class containing left and right child of current
node and key value*/
class Node
{
int data;
Node left, right;
public Node( int item)
{
data = item;
left = right = null ;
}
}
class BinaryTree
{
// Root of the Binary Tree
Node root;
public BinaryTree()
{
root = null ;
}
/* function to print level order traversal of tree*/
void printLevelOrder()
{
int h = height(root);
int i;
for (i= 1 ; i<=h; i++)
printGivenLevel(root, i);
}
/* Compute the "height" of a tree -- the number of
nodes along the longest path from the root node
down to the farthest leaf node.*/
int height(Node root)
{
if (root == null )
return 0 ;
else
{
/* compute height of each subtree */
int lheight = height(root.left);
int rheight = height(root.right);
/* use the larger one */
if (lheight > rheight)
return (lheight+ 1 );
else return (rheight+ 1 );
}
}
/* Print nodes at the given level */
void printGivenLevel (Node root , int level)
{
if (root == null )
return ;
if (level == 1 )
System.out.print(root.data + " " );
else if (level > 1 )
{
printGivenLevel(root.left, level- 1 );
printGivenLevel(root.right, level- 1 );
}
}
/* Driver program to test above functions */
public static void main(String args[])
{
BinaryTree tree = new BinaryTree();
tree.root= new Node( 1 );
tree.root.left= new Node( 2 );
tree.root.right= new Node( 3 );
tree.root.left.left= new Node( 4 );
tree.root.left.right= new Node( 5 );
System.out.println("Level order traversal of
binary tree is ");
tree.printLevelOrder();
}
}Python3
# Recursive Python program for level
# order traversal of Binary Tree
# A node structure
class Node:
# A utility function to create a new node
def __init__( self , key):
self .data = key
self .left = None
self .right = None
# Function to print level order traversal of tree
def printLevelOrder(root):
h = height(root)
for i in range ( 1 , h + 1 ):
printGivenLevel(root, i)
# Print nodes at a given level
def printGivenLevel(root , level):
if root is None :
return
if level = = 1 :
print (root.data, end = " " )
elif level > 1 :
printGivenLevel(root.left , level - 1 )
printGivenLevel(root.right , level - 1 )
""" Compute the height of a tree--the number of nodes
along the longest path from the root node down to
the farthest leaf node
"""
def height(node):
if node is None :
return 0
else :
# Compute the height of each subtree
lheight = height(node.left)
rheight = height(node.right)
#Use the larger one
if lheight > rheight :
return lheight + 1
else :
return rheight + 1
# Driver program to test above function
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
print ( "Level order traversal of binary tree is -" )
printLevelOrder(root)
#This code is contributed by Nikhil Kumar Singh(nickzuck_007)C#
// Recursive c# program for level
// order traversal of Binary Tree
using System;
/* Class containing left and right
child of current node and key value*/
public class Node
{
public int data;
public Node left, right;
public Node( int item)
{
data = item;
left = right = null ;
}
}
class GFG
{
// Root of the Binary Tree
public Node root;
public void BinaryTree()
{
root = null ;
}
/* function to print level order
traversal of tree*/
public virtual void printLevelOrder()
{
int h = height(root);
int i;
for (i = 1; i <= h; i++)
{
printGivenLevel(root, i);
}
}
/* Compute the "height" of a tree --
the number of nodes along the longest
path from the root node down to the
farthest leaf node.*/
public virtual int height(Node root)
{
if (root == null )
{
return 0;
}
else
{
/* compute height of each subtree */
int lheight = height(root.left);
int rheight = height(root.right);
/* use the larger one */
if (lheight > rheight)
{
return (lheight + 1);
}
else
{
return (rheight + 1);
}
}
}
/* Print nodes at the given level */
public virtual void printGivenLevel(Node root, int level)
{
if (root == null )
{
return ;
}
if (level == 1)
{
Console.Write(root.data + " " );
}
else if (level > 1)
{
printGivenLevel(root.left, level - 1);
printGivenLevel(root.right, level - 1);
}
}
// Driver Code
public static void Main( string [] args)
{
GFG tree = new GFG();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
Console.WriteLine( "Level order traversal " +
"of binary tree is " );
tree.printLevelOrder();
}
}
// This code is contributed by Shrikant13输出如下:
Level order traversal of binary tree is -
1 2 3 4 5时间复杂度:
O(n ^ 2)在最坏的情况下。对于倾斜的树, printGivenLevel()花费O(n)时间, 其中n是倾斜的树中的节点数。因此printLevelOrder()的时间复杂度为O(n)+ O(n-1)+ O(n-2)+ .. + O(1), 即O(n ^ 2)。
空间复杂度:
O(n)在最坏的情况下。对于倾斜的树, printGivenLevel()将O(n)空间用于调用堆栈。对于平衡树, 调用堆栈使用O(log n)空间(即平衡树的高度)。
方法2(使用队列)
算法:
对于每个节点, 首先访问该节点, 然后将其子节点放入FIFO队列中。
printLevelorder(tree)
1) Create an empty queue q
2) temp_node = root /*start from root*/
3) Loop while temp_node is not NULL
a) print temp_node->data.
b) Enqueue temp_node’s children (first left then right children) to q
c) Dequeue a node from q and assign it’s value to temp_node实现
这是上述算法的简单实现。使用最大大小为500的数组实现队列。我们也可以将队列实现为链表。
C ++
/* C++ program to print level
order traversal using STL */
#include <bits/stdc++.h>
using namespace std;
// A Binary Tree Node
struct Node
{
int data;
struct Node *left, *right;
};
// Iterative method to find height of Binary Tree
void printLevelOrder(Node *root)
{
// Base Case
if (root == NULL) return ;
// Create an empty queue for level order traversal
queue<Node *> q;
// Enqueue Root and initialize height
q.push(root);
while (q.empty() == false )
{
// Print front of queue and remove it from queue
Node *node = q.front();
cout << node->data << " " ;
q.pop();
/* Enqueue left child */
if (node->left != NULL)
q.push(node->left);
/*Enqueue right child */
if (node->right != NULL)
q.push(node->right);
}
}
// Utility function to create a new tree node
Node* newNode( int data)
{
Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
// Driver program to test above functions
int main()
{
// Let us create binary tree shown in above diagram
Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
cout << "Level Order traversal of binary tree is \n" ;
printLevelOrder(root);
return 0;
}C
// Iterative Queue based C program
// to do level order traversal
// of Binary Tree
#include <stdio.h>
#include <stdlib.h>
#define MAX_Q_SIZE 500
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct node
{
int data;
struct node* left;
struct node* right;
};
/* frunction prototypes */
struct node** createQueue( int *, int *);
void enQueue( struct node **, int *, struct node *);
struct node *deQueue( struct node **, int *);
/* Given a binary tree, print its nodes in level order
using array for implementing queue */
void printLevelOrder( struct node* root)
{
int rear, front;
struct node **queue = createQueue(&front, &rear);
struct node *temp_node = root;
while (temp_node)
{
printf ( "%d " , temp_node->data);
/*Enqueue left child */
if (temp_node->left)
enQueue(queue, &rear, temp_node->left);
/*Enqueue right child */
if (temp_node->right)
enQueue(queue, &rear, temp_node->right);
/*Dequeue node and make it temp_node*/
temp_node = deQueue(queue, &front);
}
}
/*UTILITY FUNCTIONS*/
struct node** createQueue( int *front, int *rear)
{
struct node **queue =
( struct node **) malloc ( sizeof ( struct node*)
*MAX_Q_SIZE);
*front = *rear = 0;
return queue;
}
void enQueue( struct node **queue, int *rear, struct node *new_node)
{
queue[*rear] = new_node;
(*rear)++;
}
struct node *deQueue( struct node **queue, int *front)
{
(*front)++;
return queue[*front - 1];
}
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newNode( int data)
{
struct node* node = ( struct node*)
malloc ( sizeof ( struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
/* Driver program to test above functions*/
int main()
{
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
printf ( "Level Order traversal of binary tree is \n" );
printLevelOrder(root);
return 0;
}Java
// Iterative Queue based Java program
// to do level order traversal
// of Binary Tree
/* importing the inbuilt java classes
required for the program */
import java.util.Queue;
import java.util.LinkedList;
/* Class to represent Tree node */
class Node {
int data;
Node left, right;
public Node( int item) {
data = item;
left = null ;
right = null ;
}
}
/* Class to print Level Order Traversal */
class BinaryTree {
Node root;
/* Given a binary tree. Print
its nodes in level order
using array for implementing queue */
void printLevelOrder()
{
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
while (!queue.isEmpty())
{
/* poll() removes the present head.
For more information on poll() visit
http://www.lsbin.com/java/
util/linkedlist_poll.htm */
Node tempNode = queue.poll();
System.out.print(tempNode.data + " " );
/*Enqueue left child */
if (tempNode.left != null ) {
queue.add(tempNode.left);
}
/*Enqueue right child */
if (tempNode.right != null ) {
queue.add(tempNode.right);
}
}
}
public static void main(String args[])
{
/* creating a binary tree and entering
the nodes */
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node( 1 );
tree_level.root.left = new Node( 2 );
tree_level.root.right = new Node( 3 );
tree_level.root.left.left = new Node( 4 );
tree_level.root.left.right = new Node( 5 );
System.out.println("Level order traversal
of binary tree is - ");
tree_level.printLevelOrder();
}
}Python3
# Python program to print level
# order traversal using Queue
# A node structure
class Node:
# A utility function to create a new node
def __init__( self , key):
self .data = key
self .left = None
self .right = None
# Iterative Method to print the
# height of a binary tree
def printLevelOrder(root):
# Base Case
if root is None :
return
# Create an empty queue
# for level order traversal
queue = []
# Enqueue Root and initialize height
queue.append(root)
while ( len (queue) > 0 ):
# Print front of queue and
# remove it from queue
print (queue[ 0 ].data)
node = queue.pop( 0 )
#Enqueue left child
if node.left is not None :
queue.append(node.left)
# Enqueue right child
if node.right is not None :
queue.append(node.right)
#Driver Program to test above function
root = Node( 1 )
root.left = Node( 2 )
root.right = Node( 3 )
root.left.left = Node( 4 )
root.left.right = Node( 5 )
print ( "Level Order Traversal of binary tree is -" )
printLevelOrder(root)
#This code is contributed by Nikhil Kumar Singh(nickzuck_007)C#
// Iterative Queue based C# program
// to do level order traversal
// of Binary Tree
using System;
using System.Collections.Generic;
/* Class to represent Tree node */
public class Node
{
public int data;
public Node left, right;
public Node( int item)
{
data = item;
left = null ;
right = null ;
}
}
/* Class to print Level Order Traversal */
public class BinaryTree
{
Node root;
/* Given a binary tree. Print
its nodes in level order using
array for implementing queue */
void printLevelOrder()
{
Queue<Node> queue = new Queue<Node>();
queue.Enqueue(root);
while (queue.Count != 0)
{
/* poll() removes the present head.
For more information on poll() visit
http://www.lsbin.com/
java/util/linkedlist_poll.htm */
Node tempNode = queue.Dequeue();
Console.Write(tempNode.data + " " );
/*Enqueue left child */
if (tempNode.left != null )
{
queue.Enqueue(tempNode.left);
}
/*Enqueue right child */
if (tempNode.right != null )
{
queue.Enqueue(tempNode.right);
}
}
}
// Driver code
public static void Main()
{
/* creating a binary tree and entering
the nodes */
BinaryTree tree_level = new BinaryTree();
tree_level.root = new Node(1);
tree_level.root.left = new Node(2);
tree_level.root.right = new Node(3);
tree_level.root.left.left = new Node(4);
tree_level.root.left.right = new Node(5);
Console.WriteLine( "Level order traversal " +
"of binary tree is - " );
tree_level.printLevelOrder();
}
}
/* This code contributed by PrinciRaj1992 */输出如下:
Level order traversal of binary tree is -
1 2 3 4 5时间复杂度:O(n)其中n是二叉树中的节点数
空间复杂度:O(n)其中n是二叉树中的节点数
参考文献:
http://en.wikipedia.org/wiki/Breadth-first_traversal
如果你发现上述程序/算法或其他解决同一问题的方法有任何错误, 请发表评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)