本文概述
像合并排序, QuickSort是分治算法的一个例子。它选择一个元素作为枢轴, 并围绕拾取的枢轴对给定数组进行分区。quickSort有许多不同的版本, 它们以不同的方式选择枢轴。
- 始终选择第一个元素作为枢轴。
- 始终选择最后一个元素作为枢轴(在下面实现)
- 选择一个随机元素作为枢轴。
- 选择中位数作为枢轴。
quickSort中的关键过程是partition()。分区的目标是, 给定一个数组和一个数组元素x作为枢轴, 将x放在已排序数组中的正确位置, 并将所有较小的元素(小于x)放在x之前, 并将所有较大的元素(大于x)放在之后X。所有这些都应在线性时间内完成。
递归QuickSort函数的伪代码:
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}
分割算法
进行分区的方法有很多, 下面的伪代码采用CLRS书中给出的方法。逻辑很简单, 我们从最左边的元素开始, 然后将较小(或等于)元素的索引记为i。遍历时, 如果找到较小的元素, 则将当前元素与arr [i]交换。否则, 我们将忽略当前元素。
/* low --> Starting index, high --> Ending index */
quickSort(arr[], low, high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is now
at right place */
pi = partition(arr, low, high);
quickSort(arr, low, pi - 1); // Before pi
quickSort(arr, pi + 1, high); // After pi
}
}partition()的伪代码
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
partition (arr[], low, high)
{
// pivot (Element to be placed at right position)
pivot = arr[high];
i = (low - 1) // Index of smaller element
for (j = low; j <= high- 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap arr[i] and arr[j]
}
}
swap arr[i + 1] and arr[high])
return (i + 1)
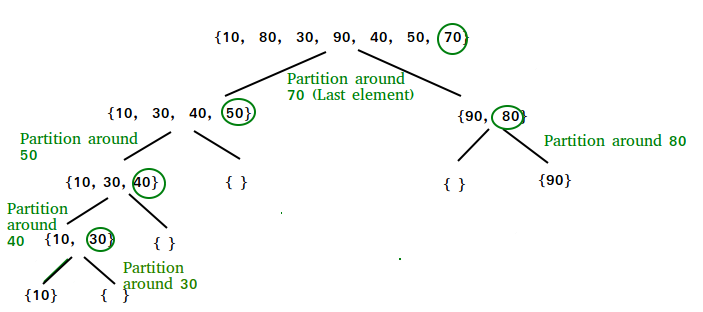
}partition()的插图:
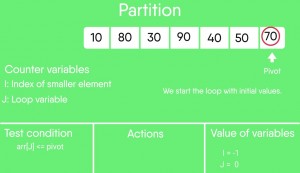
arr[] = {10, 80, 30, 90, 40, 50, 70}
Indexes: 0 1 2 3 4 5 6
low = 0, high = 6, pivot = arr[h] = 70
Initialize index of smaller element, i = -1
Traverse elements from j = low to high-1
j = 0 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 0
arr[] = {10, 80, 30, 90, 40, 50, 70} // No change as i and j
// are same
j = 1 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
j = 2 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 1
arr[] = {10, 30, 80, 90, 40, 50, 70} // We swap 80 and 30
j = 3 : Since arr[j] > pivot, do nothing
// No change in i and arr[]
j = 4 : Since arr[j] <= pivot, do i++ and swap(arr[i], arr[j])
i = 2
arr[] = {10, 30, 40, 90, 80, 50, 70} // 80 and 40 Swapped
j = 5 : Since arr[j] <= pivot, do i++ and swap arr[i] with arr[j]
i = 3
arr[] = {10, 30, 40, 50, 80, 90, 70} // 90 and 50 Swapped
We come out of loop because j is now equal to high-1.
Finally we place pivot at correct position by swapping
arr[i+1] and arr[high] (or pivot)
arr[] = {10, 30, 40, 50, 70, 90, 80} // 80 and 70 Swapped
Now 70 is at its correct place. All elements smaller than
70 are before it and all elements greater than 70 are after
it.以下是QuickSort的实现:
C ++
/* C++ implementation of QuickSort */
#include <bits/stdc++.h>
using namespace std;
// A utility function to swap two elements
void swap( int * a, int * b)
{
int t = *a;
*a = *b;
*b = t;
}
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition ( int arr[], int low, int high)
{
int pivot = arr[high]; // pivot
int i = (low - 1); // Index of smaller element
for ( int j = low; j <= high - 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* The main function that implements QuickSort
arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */
void quickSort( int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr is now
at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray( int arr[], int size)
{
int i;
for (i = 0; i < size; i++)
cout << arr[i] << " " ;
cout << endl;
}
// Driver Code
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof (arr) / sizeof (arr[0]);
quickSort(arr, 0, n - 1);
cout << "Sorted array: \n" ;
printArray(arr, n);
return 0;
}
// This code is contributed by rathbhupendra
C
/* C implementation QuickSort */
#include<stdio.h>
// A utility function to swap two elements
void swap( int * a, int * b)
{
int t = *a;
*a = *b;
*b = t;
}
/* This function takes last element as pivot, places
the pivot element at its correct position in sorted
array, and places all smaller (smaller than pivot)
to left of pivot and all greater elements to right
of pivot */
int partition ( int arr[], int low, int high)
{
int pivot = arr[high]; // pivot
int i = (low - 1); // Index of smaller element
for ( int j = low; j <= high- 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
/* The main function that implements QuickSort
arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */
void quickSort( int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr is now
at right place */
int pi = partition(arr, low, high);
// Separately sort elements before
// partition and after partition
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
/* Function to print an array */
void printArray( int arr[], int size)
{
int i;
for (i=0; i < size; i++)
printf ( "%d " , arr[i]);
printf ( "\n" );
}
// Driver program to test above functions
int main()
{
int arr[] = {10, 7, 8, 9, 1, 5};
int n = sizeof (arr)/ sizeof (arr[0]);
quickSort(arr, 0, n-1);
printf ( "Sorted array: \n" );
printArray(arr, n);
return 0;
}
Java
// Java program for implementation of QuickSort
class QuickSort
{
/* This function takes last element as pivot, places the pivot element at its correct
position in sorted array, and places all
smaller (smaller than pivot) to left of
pivot and all greater elements to right
of pivot */
int partition( int arr[], int low, int high)
{
int pivot = arr[high];
int i = (low- 1 ); // index of smaller element
for ( int j=low; j<high; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++;
// swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp = arr[i+ 1 ];
arr[i+ 1 ] = arr[high];
arr[high] = temp;
return i+ 1 ;
}
/* The main function that implements QuickSort()
arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */
void sort( int arr[], int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is
now at right place */
int pi = partition(arr, low, high);
// Recursively sort elements before
// partition and after partition
sort(arr, low, pi- 1 );
sort(arr, pi+ 1 , high);
}
}
/* A utility function to print array of size n */
static void printArray( int arr[])
{
int n = arr.length;
for ( int i= 0 ; i<n; ++i)
System.out.print(arr[i]+ " " );
System.out.println();
}
// Driver program
public static void main(String args[])
{
int arr[] = { 10 , 7 , 8 , 9 , 1 , 5 };
int n = arr.length;
QuickSort ob = new QuickSort();
ob.sort(arr, 0 , n- 1 );
System.out.println( "sorted array" );
printArray(arr);
}
}
/*This code is contributed by Rajat Mishra */python
# Python program for implementation of Quicksort Sort
# This function takes last element as pivot, places
# the pivot element at its correct position in sorted
# array, and places all smaller (smaller than pivot)
# to left of pivot and all greater elements to right
# of pivot
def partition(arr, low, high):
i = ( low - 1 ) # index of smaller element
pivot = arr[high] # pivot
for j in range (low , high):
# If current element is smaller than the pivot
if arr[j] < pivot:
# increment index of smaller element
i = i + 1
arr[i], arr[j] = arr[j], arr[i]
arr[i + 1 ], arr[high] = arr[high], arr[i + 1 ]
return ( i + 1 )
# The main function that implements QuickSort
# arr[] --> Array to be sorted, # low --> Starting index, # high --> Ending index
# Function to do Quick sort
def quickSort(arr, low, high):
if low < high:
# pi is partitioning index, arr is now
# at right place
pi = partition(arr, low, high)
# Separately sort elements before
# partition and after partition
quickSort(arr, low, pi - 1 )
quickSort(arr, pi + 1 , high)
# Driver code to test above
arr = [ 10 , 7 , 8 , 9 , 1 , 5 ]
n = len (arr)
quickSort(arr, 0 , n - 1 )
print ( "Sorted array is:" )
for i in range (n):
print ( "%d" % arr[i]), # This code is contributed by Mohit Kumra
C#
// C# program for implementation of QuickSort
using System;
class GFG {
/* This function takes last element as pivot, places the pivot element at its correct
position in sorted array, and places all
smaller (smaller than pivot) to left of
pivot and all greater elements to right
of pivot */
static int partition( int []arr, int low, int high)
{
int pivot = arr[high];
// index of smaller element
int i = (low - 1);
for ( int j = low; j < high; j++)
{
// If current element is smaller
// than the pivot
if (arr[j] < pivot)
{
i++;
// swap arr[i] and arr[j]
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
// swap arr[i+1] and arr[high] (or pivot)
int temp1 = arr[i+1];
arr[i+1] = arr[high];
arr[high] = temp1;
return i+1;
}
/* The main function that implements QuickSort()
arr[] --> Array to be sorted, low --> Starting index, high --> Ending index */
static void quickSort( int []arr, int low, int high)
{
if (low < high)
{
/* pi is partitioning index, arr[pi] is
now at right place */
int pi = partition(arr, low, high);
// Recursively sort elements before
// partition and after partition
quickSort(arr, low, pi-1);
quickSort(arr, pi+1, high);
}
}
// A utility function to print array of size n
static void printArray( int []arr, int n)
{
for ( int i = 0; i < n; ++i)
Console.Write(arr[i] + " " );
Console.WriteLine();
}
// Driver program
public static void Main()
{
int []arr = {10, 7, 8, 9, 1, 5};
int n = arr.Length;
quickSort(arr, 0, n-1);
Console.WriteLine( "sorted array " );
printArray(arr, n);
}
}
// This code is contributed by Sam007.输出如下:
Sorted array:
1 5 7 8 9 10QuickSort分析
通常, QuickSort所花费的时间可以编写如下。
T(n) = T(k) + T(n-k-1) + (n)前两个术语用于两个递归调用, 最后一个术语用于分区过程。 k是小于枢轴的元素数。
QuickSort花费的时间取决于输入阵列和分区策略。以下是三种情况。
最坏的情况下:最坏的情况发生在分区过程始终选择最大或最小元素作为枢轴时。如果我们考虑以上总是将最后一个元素选作枢轴的分区策略, 则当数组已经按升序或降序排序时, 最坏的情况就会发生。以下是最坏情况下的重复发生。
T(n) = T(0) + T(n-1) + (n)
which is equivalent to
T(n) = T(n-1) + (n)上述递归式的解为0(n2)。
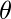
最佳情况:最好的情况是分区过程始终选择中间元素作为枢轴。以下是最佳情况的重复发生。
T(n) = 2T(n/2) + (n)以上递归的解决方法是
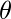
上述递归式的解是0(nLogn)。它可以用主定理的情形2来解决。
平均情况:
为了进行平均情况分析,我们需要考虑所有可能的数组排列,并计算每个排列所花费的时间,这看起来并不容易。
通过考虑分区将O(n / 9)元素放在一个集合中而将O(9n / 10)元素放在另一个集合中的情况, 我们可以获得平均情况的想法。以下是这种情况的重复发生。
T(n) = T(n/9) + T(9n/10) + (n)上述重复的解决方案也是O(nLogn)
尽管QuickSort在最坏情况下的时间复杂度为O(n2)比其他许多排序算法(例如合并排序和堆排序, QuickSort在实践中会更快, 因为它的内部循环可以在大多数体系结构和大多数实际数据中有效地实现。通过更改数据透视表的选择, 可以以不同的方式实现QuickSort, 因此对于给定类型的数据, 最坏的情况很少发生。但是, 当数据量巨大并存储在外部存储中时, 通常认为合并排序更好。
QuickSort稳定吗?
默认实现不稳定。但是, 通过将索引视为比较参数, 可以使任何排序算法保持稳定。
快速排序就地吗?
根据就地算法的广义定义, 它有资格作为就地排序算法, 因为它仅使用额外的空间来存储递归函数调用, 而不使用操纵输入。
什么是3向QuickSort?
在简单的QuickSort算法中, 我们选择一个元素作为枢轴, 围绕枢轴对数组进行分区, 并在枢轴的左右两侧递归子数组。
考虑具有许多冗余元素的阵列。例如, {1, 4, 2, 4, 2, 4, 1, 2, 4, 1, 2, 2, 2, 2, 4, 1, 1, 4, 4, 4}。如果在Simple QuickSort中将4选作枢轴, 我们将只修复1个4并递归处理剩余的事件。在3 Way QuickSort中, 数组arr [l..r]分为3部分:
a)小于枢轴的arr [l..i]元素。
b)arr [i + 1..j-1]元素等于数据透视。
c)大于枢轴的arr [j..r]元素。
如何实现链表的QuickSort?
单链接列表上的QuickSort
双链表上的QuickSort
我们可以迭代地实现QuickSort吗?
是的, 请参考:迭代快速排序
为什么快速排序优先于MergeSort来对数组进行排序
快速排序的一般形式是就地排序(即不需要任何额外的存储空间), 而合并排序则需要O(N)的额外存储空间, N表示数组大小, 这可能会非常昂贵。分配和取消分配用于合并排序的额外空间会增加算法的运行时间。比较平均复杂度, 我们发现两种类型的排序均具有O(NlogN)平均复杂度, 但常量不同。对于阵列, 由于使用了额外的O(N)存储空间, 合并排序会丢失。
快速排序的大多数实际实现使用随机版本。随机版本的预期时间复杂度为O(nLogn)。随机版本也可能出现最坏的情况, 但是对于特定模式(如排序数组)不会发生最坏情况, 并且随机快速排序在实践中效果很好。
快速排序也是一种缓存友好的排序算法, 因为它在用于数组时具有良好的引用局部性。
快速排序也是尾部递归的, 因此完成了尾部调用优化。
为什么对于链接列表, 首选MergeSort而不是QuickSort?
对于链表, 情况有所不同, 主要是由于数组和链表的内存分配不同。与数组不同, 链接列表节点在内存中可能不相邻。与数组不同, 在链表中, 我们可以在O(1)额外空间和O(1)时间的中间插入项目。因此, 可以实现合并排序的合并操作而不必为链接列表增加空间。
在数组中, 由于元素在内存中是连续的, 因此我们可以进行随机访问。假设我们有一个整数(4字节)数组A, 并且将A [0]的地址设为x, 然后访问A [i], 我们可以直接访问(x + i * 4)处的内存。与数组不同, 我们不能在链表中进行随机访问。快速排序需要很多此类访问权限。在链接列表中, 要访问第i个索引, 由于没有连续的内存块, 我们必须将每个节点从头到第i个节点。因此, 用于快速分类的开销增加了。合并排序顺序访问数据, 并且对随机访问的需求低。
如何优化QuickSort, 以便在最坏的情况下占用O(Log n)额外的空间?
请参阅:QuickSort尾部调用优化(将最坏情况的空间减少到Log n)
图解:

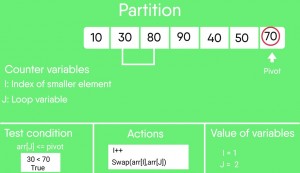
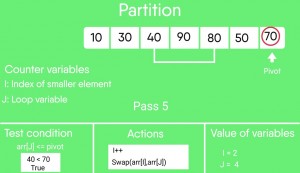




- 快速排序测验
- 有关QuickSort的最新文章
- 排序的编码实践。
参考文献:
http://en.wikipedia.org/wiki/Quicksort
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)