算法题：如何使用高斯消除法求解线性方程？

2021年4月2日11:27:06 发表评论 1,010 次浏览

本文概述

这篇文章着重于用一种算法来求解线性方程组。我们将处理系数矩阵。高斯消去对奇异矩阵不起作用(它们导致除零)。

Input: For N unknowns, input is an augmented 
       matrix of size N x (N+1). One extra 
       column is for Right Hand Side (RHS)
  mat[N][N+1] = {{3.0, 2.0, -4.0, 3.0}, {2.0, 3.0, 3.0, 15.0}, {5.0, -3, 1.0, 14.0}
               };
Output: Solution to equations is:
        3.000000
        1.000000
        2.000000

Explanation:
Given matrix represents following equations
3.0X1 + 2.0X2 - 4.0X3 =  3.0
2.0X1 + 3.0X2 + 3.0X3 = 15.0
5.0X1 - 3.0X2 +    X3 = 14.0

There is a unique solution for given equations, solutions is, X1 = 3.0, X2 = 1.0, X3 = 2.0,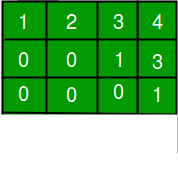
矩阵11

行阶梯形:如果满足以下条件，则称矩阵处于r.e.f.中:

  1. 每行中的第一个非零元素(称为前导系数)为1。
  2. 每个前导系数位于前一行前导系数右侧的一栏中。
  3. 具有全零的行位于具有至少一个非零元素的行的下方。
矩阵1

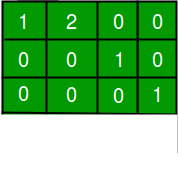
简化的行阶梯形形式：

据说Matrix位于r.r.e.f.如果符合以下条件, 则–

  1. r.e.f.的所有条件
  2. 每行中的前导系数是其列中唯一的非零条目。

该算法主要是关于在矩阵的行上执行一系列操作。在执行这些操作时, 我们要记住的是, 我们希望将矩阵转换为行阶梯形形式的上三角矩阵。操作可以是：

  1. 交换两行
  2. 将行乘以非零标量
  3. 将另一行的倍数添加到一行

过程：

  1. 向前消除：简化为行阶梯形形式。使用它可以告诉你是否存在解决方案, 唯一解决方案或无限多个解决方案。
  2. 反向替换：进一步简化为简化的行阶梯形形式。

算法：

  1. 部分枢轴：通过交换行来查找第k个枢轴, 以将绝对值最大的条目移动到枢轴位置。这使算法具有计算稳定性。
  2. 对于枢轴以下的每一行, 计算使第k个条目为零的因子f, 并为该行中的每个元素减去第k行中相应元素的f倍。
  3. 对每个未知重复上述步骤。我们将获得部分R.e.f.矩阵。

下面是上述算法的实现。

C

// C++ program to demonstrate working of Guassian Elimination
// method
#include<bits/stdc++.h>
using namespace std;
  
#define N 3        // Number of unknowns
  
// function to reduce matrix to r.e.f.  Returns a value to 
// indicate whether matrix is singular or not
int forwardElim( double mat[N][N+1]);
  
// function to calculate the values of the unknowns
void backSub( double mat[N][N+1]);
  
// function to get matrix content
void gaussianElimination( double mat[N][N+1])
{
     /* reduction into r.e.f. */
     int singular_flag = forwardElim(mat);
  
     /* if matrix is singular */
     if (singular_flag != -1)
     {
         printf ( "Singular Matrix.\n" );
  
         /* if the RHS of equation corresponding to
            zero row  is 0, * system has infinitely
            many solutions, else inconsistent*/
         if (mat[singular_flag][N])
             printf ( "Inconsistent System." );
         else
             printf ( "May have infinitely many "
                    "solutions." );
  
         return ;
     }
  
     /* get solution to system and print it using
        backward substitution */
     backSub(mat);
}
  
// function for elementary operation of swapping two rows
void swap_row( double mat[N][N+1], int i, int j)
{
     //printf("Swapped rows %d and %d\n", i, j);
  
     for ( int k=0; k<=N; k++)
     {
         double temp = mat[i][k];
         mat[i][k] = mat[j][k];
         mat[j][k] = temp;
     }
}
  
// function to print matrix content at any stage
void print( double mat[N][N+1])
{
     for ( int i=0; i<N; i++, printf ( "\n" ))
         for ( int j=0; j<=N; j++)
             printf ( "%lf " , mat[i][j]);
  
     printf ( "\n" );
}
  
// function to reduce matrix to r.e.f.
int forwardElim( double mat[N][N+1])
{
     for ( int k=0; k<N; k++)
     {
         // Initialize maximum value and index for pivot
         int i_max = k;
         int v_max = mat[i_max][k];
  
         /* find greater amplitude for pivot if any */
         for ( int i = k+1; i < N; i++)
             if ( abs (mat[i][k]) > v_max)
                 v_max = mat[i][k], i_max = i;
  
         /* if a prinicipal diagonal element  is zero, * it denotes that matrix is singular, and
          * will lead to a division-by-zero later. */
         if (!mat[k][i_max])
             return k; // Matrix is singular
  
         /* Swap the greatest value row with current row */
         if (i_max != k)
             swap_row(mat, k, i_max);
  
  
         for ( int i=k+1; i<N; i++)
         {
             /* factor f to set current row kth element to 0, * and subsequently remaining kth column to 0 */
             double f = mat[i][k]/mat[k][k];
  
             /* subtract fth multiple of corresponding kth
                row element*/
             for ( int j=k+1; j<=N; j++)
                 mat[i][j] -= mat[k][j]*f;
  
             /* filling lower triangular matrix with zeros*/
             mat[i][k] = 0;
         }
  
         //print(mat);        //for matrix state
     }
     //print(mat);            //for matrix state
     return -1;
}
  
// function to calculate the values of the unknowns
void backSub( double mat[N][N+1])
{
     double x[N];  // An array to store solution
  
     /* Start calculating from last equation up to the
        first */
     for ( int i = N-1; i >= 0; i--)
     {
         /* start with the RHS of the equation */
         x[i] = mat[i][N];
  
         /* Initialize j to i+1 since matrix is upper
            triangular*/
         for ( int j=i+1; j<N; j++)
         {
             /* subtract all the lhs values
              * except the coefficient of the variable
              * whose value is being calculated */
             x[i] -= mat[i][j]*x[j];
         }
  
         /* divide the RHS by the coefficient of the
            unknown being calculated */
         x[i] = x[i]/mat[i][i];
     }
  
     printf ( "\nSolution for the system:\n" );
     for ( int i=0; i<N; i++)
         printf ( "%lf\n" , x[i]);
}
  
// Driver program
int main()
{
     /* input matrix */
     double mat[N][N+1] = {{3.0, 2.0, -4.0, 3.0}, {2.0, 3.0, 3.0, 15.0}, {5.0, -3, 1.0, 14.0}
                          };
  
     gaussianElimination(mat);
  
     return 0;
}

的PHP

<?php
// PHP program to demonstrate working 
// of Guassian Elimination method
  
$N = 3; // Number of unknowns
  
  
// function to get matrix content
function gaussianElimination( $mat )
{
     global $N ;
      
     /* reduction into r.e.f. */
     $singular_flag = forwardElim( $mat );
  
     /* if matrix is singular */
     if ( $singular_flag != -1)
     {
         print ( "Singular Matrix.\n" );
  
         /* if the RHS of equation corresponding to
         zero row is 0, * system has infinitely
         many solutions, else inconsistent*/
         if ( $mat [ $singular_flag ][ $N ])
             print ( "Inconsistent System." );
         else
             print ( "May have infinitely many solutions." );
  
         return ;
     }
  
     /* get solution to system and print it using
     backward substitution */
     backSub( $mat );
}
  
// function for elementary operation
// of swapping two rows
function swap_row(& $mat , $i , $j )
{
     global $N ;
     //printf("Swapped rows %d and %d\n", i, j);
  
     for ( $k = 0; $k <= $N ; $k ++)
     {
         $temp = $mat [ $i ][ $k ];
         $mat [ $i ][ $k ] = $mat [ $j ][ $k ];
         $mat [ $j ][ $k ] = $temp ;
     }
}
  
// function to print matrix content at any stage
function print1( $mat )
{
     global $N ;
     for ( $i =0; $i < $N ; $i ++, print ( "\n" ))
         for ( $j =0; $j <= $N ; $j ++)
             print ( $mat [ $i ][ $j ]);
  
     print ( "\n" );
}
  
// function to reduce matrix to r.e.f.
function forwardElim(& $mat )
{
     global $N ;
     for ( $k =0; $k < $N ; $k ++)
     {
         // Initialize maximum value and index for pivot
         $i_max = $k ;
         $v_max = $mat [ $i_max ][ $k ];
  
         /* find greater amplitude for pivot if any */
         for ( $i = $k +1; $i < $N ; $i ++)
             if ( abs ( $mat [ $i ][ $k ]) > $v_max )
                 {
                     $v_max = $mat [ $i ][ $k ];
                     $i_max = $i ;
                 }
  
         /* if a prinicipal diagonal element is zero, * it denotes that matrix is singular, and
         * will lead to a division-by-zero later. */
         if (! $mat [ $k ][ $i_max ])
             return $k ; // Matrix is singular
  
         /* Swap the greatest value row with current row */
         if ( $i_max != $k )
             swap_row( $mat , $k , $i_max );
  
  
         for ( $i = $k + 1; $i < $N ; $i ++)
         {
             /* factor f to set current row kth element to 0, * and subsequently remaining kth column to 0 */
             $f = $mat [ $i ][ $k ]/ $mat [ $k ][ $k ];
  
             /* subtract fth multiple of corresponding kth
             row element*/
             for ( $j = $k + 1; $j <= $N ; $j ++)
                 $mat [ $i ][ $j ] -= $mat [ $k ][ $j ] * $f ;
  
             /* filling lower triangular matrix with zeros*/
             $mat [ $i ][ $k ] = 0;
         }
  
         //print(mat); //for matrix state
     }
     //print(mat);     //for matrix state
     return -1;
}
  
// function to calculate the values of the unknowns
function backSub(& $mat )
{
     global $N ;
     $x = array_fill (0, $N , 0); // An array to store solution
  
     /* Start calculating from last equation up to the
     first */
     for ( $i = $N - 1; $i >= 0; $i --)
     {
         /* start with the RHS of the equation */
         $x [ $i ] = $mat [ $i ][ $N ];
  
         /* Initialize j to i+1 since matrix is upper
         triangular*/
         for ( $j = $i + 1; $j < $N ; $j ++)
         {
             /* subtract all the lhs values
             * except the coefficient of the variable
             * whose value is being calculated */
             $x [ $i ] -= $mat [ $i ][ $j ] * $x [ $j ];
         }
  
         /* divide the RHS by the coefficient of the
         unknown being calculated */
         $x [ $i ] = $x [ $i ] / $mat [ $i ][ $i ];
     }
  
     print ( "\nSolution for the system:\n" );
     for ( $i = 0; $i < $N ; $i ++)
         print (number_format( strval ( $x [ $i ]), 6). "\n" );
}
  
// Driver program
  
     /* input matrix */
     $mat = array ( array (3.0, 2.0, -4.0, 3.0), array (2.0, 3.0, 3.0, 15.0), array (5.0, -3, 1.0, 14.0));
  
     gaussianElimination( $mat );
  
// This code is contributed by mits
?>

输出如下：

Solution for the system:
3.000000
1.000000
2.000000

插图：

处理

时间复杂度：由于对于每个枢轴, 我们遍历该零件在其下面的每一行的右侧, 因此O(n)*(O(n)* O(n))= O(n3)。

我们还可以应用高斯消去法来计算：

  1. 矩阵的等级
  2. 矩阵的行列式
  3. 可逆方阵的逆

本文作者：Yash Varyani。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: