质因子分解：求一个数的质数因子

2021年4月2日10:55:52 发表评论 1,747 次浏览

本文概述

质数因子是指给定的质数的因数。因式就是把数相乘得到另一个数。简单地说，质数因子就是找出哪些质数相乘得到原来的数。

例子：

例:15的质数因子是3和5(因为3×5=15, 3和5是质数)。

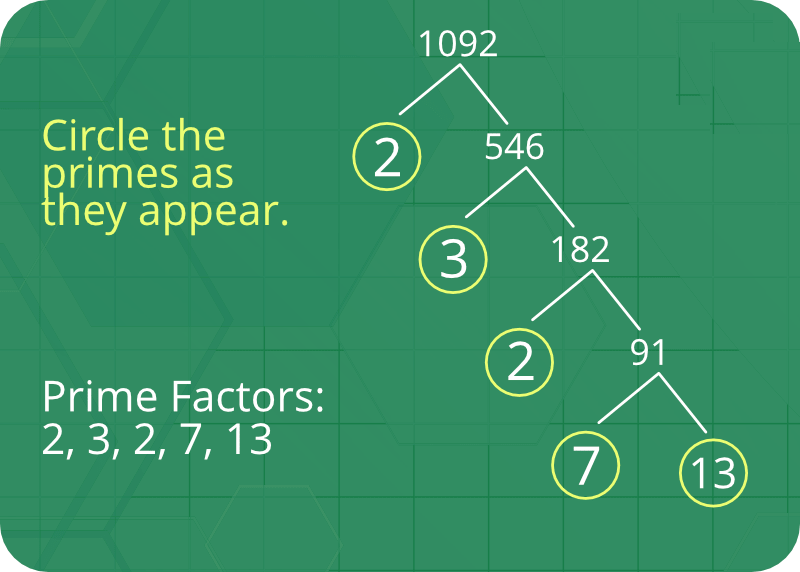
质因子分解

关于质数因子的一些有趣的事实：

  1. 对于任何数量, 只有一组(唯一！)素数因子。
  2. 为了保持唯一素数分解的这一特性, 必须将数字1既不是素数也不是复合数。
  3. 素因式分解可以帮助我们进行除数运算, 简化分数并找到分数的公共分母。
  4. Pollard的Rho是素数分解算法, 对于大型复合数与小的主要因素。
  5. 密码学是对密码的研究。素数分解对于尝试根据数字创建(或破解)秘密代码的人们非常重要。

如何打印一个数的质数因子？

天真的解决方案：

给定一个数字n, 编写一个函数打印n的所有素数。例如, 如果输入数字为12,

那么输出应该是" 2 2 3", 如果输入数字是315, 那么输出应该是" 3 3 5 7"。

以下是查找所有主要因素的步骤：

  1. 当n被2整除时，打印2并将n除以2。。
  2. 步骤1之后，n必须为奇数。现在开始一个循环，从i = 3到n的平方根。当i除以n时，打印i并将n除以i，将i增加2，然后继续。
  3. 如果n是一个质数并且大于2，那么n在以上两步之后不会变成1。如果n大于2，输出n。

C/C++

// Program to print all prime factors
# include <stdio.h>
# include <math.h>
  
// A function to print all prime factors of a given number n
void primeFactors( int n)
{
     // Print the number of 2s that divide n
     while (n%2 == 0)
     {
         printf ( "%d " , 2);
         n = n/2;
     }
  
     // n must be odd at this point.  So we can skip 
     // one element (Note i = i +2)
     for ( int i = 3; i <= sqrt (n); i = i+2)
     {
         // While i divides n, print i and divide n
         while (n%i == 0)
         {
             printf ( "%d " , i);
             n = n/i;
         }
     }
  
     // This condition is to handle the case when n 
     // is a prime number greater than 2
     if (n > 2)
         printf ( "%d " , n);
}
  
/* Driver program to test above function */
int main()
{
     int n = 315;
     primeFactors(n);
     return 0;
}

Java

// Program to print all prime factors
import java.io.*;
import java.lang.Math;
  
class GFG {
     // A function to print all prime factors
     // of a given number n
     public static void primeFactors( int n)
     {
         // Print the number of 2s that divide n
         while (n % 2 == 0 ) {
             System.out.print( 2 + " " );
             n /= 2 ;
         }
  
         // n must be odd at this point.  So we can
         // skip one element (Note i = i +2)
         for ( int i = 3 ; i <= Math.sqrt(n); i += 2 ) {
             // While i divides n, print i and divide n
             while (n % i == 0 ) {
                 System.out.print(i + " " );
                 n /= i;
             }
         }
  
         // This condition is to handle the case whien
         // n is a prime number greater than 2
         if (n > 2 )
             System.out.print(n);
     }
  
     public static void main(String[] args)
     {
         int n = 315 ;
         primeFactors(n);
     }
}

python

# Python program to print prime factors
  
import math
  
# A function to print all prime factors of 
# a given number n
def primeFactors(n):
      
     # Print the number of two's that divide n
     while n % 2 = = 0 :
         print 2 , n = n / 2
          
     # n must be odd at this point
     # so a skip of 2 ( i = i + 2) can be used
     for i in range ( 3 , int (math.sqrt(n)) + 1 , 2 ):
          
         # while i divides n, print i ad divide n
         while n % i = = 0 :
             print i, n = n / i
              
     # Condition if n is a prime
     # number greater than 2
     if n > 2 :
         print n
          
# Driver Program to test above function
  
n = 315
primeFactors(n)
  
# This code is contributed by Harshit Agrawal

C#

// C# Program to print all prime factors
using System;
  
namespace prime {
public class GFG {
  
     // A function to print all prime
     // factors of a given number n
     public static void primeFactors( int n)
     {
         // Print the number of 2s that divide n
         while (n % 2 == 0) {
             Console.Write(2 + " " );
             n /= 2;
         }
  
         // n must be odd at this point. So we can
         // skip one element (Note i = i +2)
         for ( int i = 3; i <= Math.Sqrt(n); i += 2) {
             // While i divides n, print i and divide n
             while (n % i == 0) {
                 Console.Write(i + " " );
                 n /= i;
             }
         }
  
         // This condition is to handle the case whien
         // n is a prime number greater than 2
         if (n > 2)
             Console.Write(n);
     }
  
     // Driver Code
     public static void Main()
     {
         int n = 315;
         primeFactors(n);
     }
}
}
  
// This code is contributed by Sam007

PHP

<?php
// PHP Efficient program to print all
// prime factors of a given number
  
// function to print all prime 
// factors of a given number n
function primeFactors( $n )
{
      
     // Print the number of
     // 2s that divide n
     while ( $n % 2 == 0)
     {
         echo 2, " " ;
         $n = $n / 2;
     }
  
     // n must be odd at this 
     // point. So we can skip 
     // one element (Note i = i +2)
     for ( $i = 3; $i <= sqrt( $n ); 
                    $i = $i + 2)
     {
          
         // While i divides n, // print i and divide n
         while ( $n % $i == 0)
         {
             echo $i , " " ;
             $n = $n / $i ;
         }
     }
  
     // This condition is to 
     // handle the case when n 
     // is a prime number greater
     // than 2
     if ( $n > 2)
         echo $n , " " ;
}
  
     // Driver Code
     $n = 315;
     primeFactors( $n );
  
// This code is contributed by aj_36
?>

输出如下：

3 3 5 7

这是如何运作的？

步骤1和2处理合数步骤3处理质数。为了证明完整的算法是可行的，我们需要证明步骤1和2实际上是处理合数的。

现在主要的部分是，循环运行到n的平方根。为了证明这个优化是有效的，让我们考虑以下合数的性质。

每个复合数至少具有一个小于或等于其平方根的素数。

可以使用计数器语句证明此属性。令a和b为n的两个因数, 使得a * b = n。如果两者均大于√n, 则a.b>√n, *√n, 这与表达式" a * b = n"相矛盾。

在上述算法的第2步中, 我们运行一个循环并执行以下操作-

  • 找到最小素数因子i(必须小于√n, )
  • 重复将n除以i, 从n中删除所有出现的i。
  • 重复步骤a和b, 除以n, i = i +2。重复步骤a和b, 直到n变为1或质数。

高效的解决方案：

找出数字素数的程序

  • 阵列产品的主要因素
  • 给定数的第N个素数
  • 程序可成对打印多个因子
  • 前n个自然数的不同质数的数量
  • 许多唯一素数的乘积

与素数有关的更多问题

  • 计算主要因子仅为2和3的范围中的数字
  • 两个数的共同素数
  • 直到n的数字的最小素因数
  • 数的最小除数
  • 使用素数分解的数的因子之和
  • 数字和等于其所有素数的数字之和的数字
  • 具有最大素数在M到N范围内的数字

最近关于素数的文章！

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: