本文概述
给定两个字符串str1和str2及其以下的操作,可以在str1上执行。找出将' str1 '转换为' str2 '所需的最小编辑次数(操作)。
- 插入insert
- 删除remove
- 替换replace
以上所有操作成本均相等。
例子:
Input: str1 = "geek", str2 = "gesek"
Output: 1
We can convert str1 into str2 by inserting a 's'.
Input: str1 = "cat", str2 = "cut"
Output: 1
We can convert str1 into str2 by replacing 'a' with 'u'.
Input: str1 = "sunday", str2 = "saturday"
Output: 3
Last three and first characters are same. We basically
need to convert "un" to "atur". This can be done using
below three operations.
Replace 'n' with 'r', insert t, insert a在这种情况下, 有哪些子问题?
这个想法是从两个字符串的左侧或右侧逐一处理所有字符。
让我们从右上角遍历, 遍历每对字符有两种可能性。
m: Length of str1 (first string)
n: Length of str2 (second string)- 如果两个字符串的最后一个字符相同, 则无事可做。忽略最后一个字符并获得剩余字符串的计数。因此我们重复长度为m-1和n-1。
- 否则(如果最后一个字符不同), 我们考虑对" str1"的所有操作, 考虑对第一个字符串的最后一个字符的所有三个操作, 递归计算这三个操作的最低成本, 并取三个值中的最小值。
- 插入:重复出现m和n-1
- 删除:重复执行m-1和n
- 替换:重复执行m-1和n-1
下面是上述Naive递归解决方案的C++实现。
C++
// A Naive recursive C++ program to find minimum number
// operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
// Utility function to find minimum of three numbers
int min( int x, int y, int z)
{
return min(min(x, y), z);
}
int editDist(string str1, string str2, int m, int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0)
return m;
// If last characters of two strings are same, nothing
// much to do. Ignore last characters and get count for
// remaining strings.
if (str1[m - 1] == str2[n - 1])
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all three
// operations on last character of first string, recursively
// compute minimum cost for all three operations and take
// minimum of three values.
return 1 + min(editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1, n - 1) // Replace
);
}
// Driver program
int main()
{
// your code goes here
string str1 = "sunday" ;
string str2 = "saturday" ;
cout << editDist(str1, str2, str1.length(), str2.length());
return 0;
}Java
// A Naive recursive Java program to find minimum number
// operations to convert str1 to str2
class EDIST {
static int min( int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDist(String str1, String str2, int m, int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0 )
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0 )
return m;
// If last characters of two strings are same, nothing
// much to do. Ignore last characters and get count for
// remaining strings.
if (str1.charAt(m - 1 ) == str2.charAt(n - 1 ))
return editDist(str1, str2, m - 1 , n - 1 );
// If last characters are not same, consider all three
// operations on last character of first string, recursively
// compute minimum cost for all three operations and take
// minimum of three values.
return 1 + min(editDist(str1, str2, m, n - 1 ), // Insert
editDist(str1, str2, m - 1 , n), // Remove
editDist(str1, str2, m - 1 , n - 1 ) // Replace
);
}
public static void main(String args[])
{
String str1 = "sunday" ;
String str2 = "saturday" ;
System.out.println(editDist(str1, str2, str1.length(), str2.length()));
}
}
/*This code is contributed by Rajat Mishra*/python
# A Naive recursive Python program to fin minimum number
# operations to convert str1 to str2
def editDistance(str1, str2, m, n):
# If first string is empty, the only option is to
# insert all characters of second string into first
if m = = 0 :
return n
# If second string is empty, the only option is to
# remove all characters of first string
if n = = 0 :
return m
# If last characters of two strings are same, nothing
# much to do. Ignore last characters and get count for
# remaining strings.
if str1[m - 1 ] = = str2[n - 1 ]:
return editDistance(str1, str2, m - 1 , n - 1 )
# If last characters are not same, consider all three
# operations on last character of first string, recursively
# compute minimum cost for all three operations and take
# minimum of three values.
return 1 + min (editDistance(str1, str2, m, n - 1 ), # Insert
editDistance(str1, str2, m - 1 , n), # Remove
editDistance(str1, str2, m - 1 , n - 1 ) # Replace
)
# Driver program to test the above function
str1 = "sunday"
str2 = "saturday"
print editDistance(str1, str2, len (str1), len (str2))
# This code is contributed by Bhavya JainC#
// A Naive recursive C# program to
// find minimum numberoperations
// to convert str1 to str2
using System;
class GFG {
static int min( int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDist(String str1, String str2, int m, int n)
{
// If first string is empty, the only option is to
// insert all characters of second string into first
if (m == 0)
return n;
// If second string is empty, the only option is to
// remove all characters of first string
if (n == 0)
return m;
// If last characters of two strings are same, nothing
// much to do. Ignore last characters and get count for
// remaining strings.
if (str1[m - 1] == str2[n - 1])
return editDist(str1, str2, m - 1, n - 1);
// If last characters are not same, consider all three
// operations on last character of first string, recursively
// compute minimum cost for all three operations and take
// minimum of three values.
return 1 + min(editDist(str1, str2, m, n - 1), // Insert
editDist(str1, str2, m - 1, n), // Remove
editDist(str1, str2, m - 1, n - 1) // Replace
);
}
// Driver code
public static void Main()
{
String str1 = "sunday" ;
String str2 = "saturday" ;
Console.WriteLine(editDist(str1, str2, str1.Length, str2.Length));
}
}
// This Code is Contributed by Sam007PHP
<?php
// A Naive recursive Python program
// to find minimum number operations
// to convert str1 to str2
function editDistance( $str1 , $str2 , $m , $n )
{
// If first string is empty, // the only option is to insert.
// all characters of second
// string into first
if ( $m == 0)
return $n ;
// If second string is empty, // the only option is to
// remove all characters of
// first string
if ( $n == 0)
return $m ;
// If last characters of two
// strings are same, nothing
// much to do. Ignore last
// characters and get count
// for remaining strings.
if ( $str1 [ $m - 1] == $str2 [ $n - 1])
{
return editDistance( $str1 , $str2 , $m - 1, $n - 1);
}
// If last characters are not same, // consider all three operations on
// last character of first string, // recursively compute minimum cost
// for all three operations and take
// minimum of three values.
return 1 + min(editDistance( $str1 , $str2 , $m , $n - 1), // Insert
editDistance( $str1 , $str2 , $m - 1, $n ), // Remove
editDistance( $str1 , $str2 , $m - 1, $n - 1)); // Replace
}
// Driver Code
$str1 = "sunday" ;
$str2 = "saturday" ;
echo editDistance( $str1 , $str2 , strlen ( $str1 ), strlen ( $str2 ));
// This code is contributed
// by Shivi_Aggarwal
?>输出如下:
3上述解决方案的时间复杂度是指数的。在最坏的情况下, 我们可能最终会做O(3^m)操作。当两个字符串的字符都不匹配时, 会发生最坏的情况。下面是最坏情况的递归调用图。
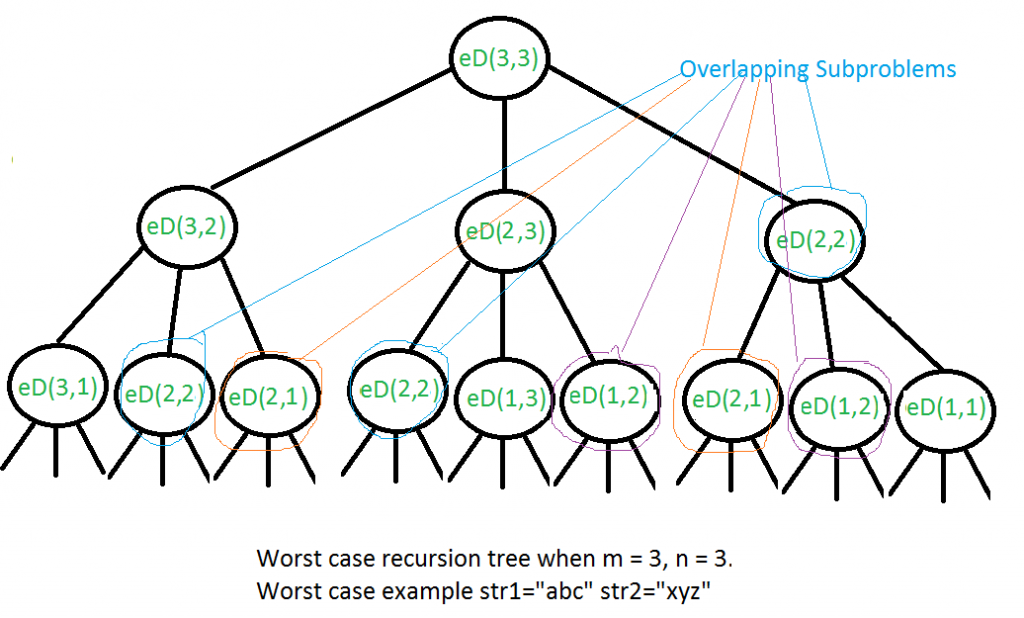
我们可以看到, 许多子问题被一次又一次地解决了, 例如, eD(2, 2)被调用了三次。由于再次调用了相同的问题, 因此此问题具有"重叠子问题"属性。因此, "编辑距离"问题具有两个属性(请参见这个和这个)的动态编程问题。像其他典型的动态编程(DP)问题一样, 可以通过构造一个存储子问题结果的临时数组来避免相同子问题的重新计算。
C++
// A Dynamic Programming based C++ program to find minimum
// number operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
// Utility function to find the minimum of three numbers
int min( int x, int y, int z)
{
return min(min(x, y), z);
}
int editDistDP(string str1, string str2, int m, int n)
{
// Create a table to store results of subproblems
int dp[m + 1][n + 1];
// Fill d[][] in bottom up manner
for ( int i = 0; i <= m; i++) {
for ( int j = 0; j <= n; j++) {
// If first string is empty, only option is to
// insert all characters of second string
if (i == 0)
dp[i][j] = j; // Min. operations = j
// If second string is empty, only option is to
// remove all characters of second string
else if (j == 0)
dp[i][j] = i; // Min. operations = i
// If last characters are same, ignore last char
// and recur for remaining string
else if (str1[i - 1] == str2[j - 1])
dp[i][j] = dp[i - 1][j - 1];
// If the last character is different, consider all
// possibilities and find the minimum
else
dp[i][j] = 1 + min(dp[i][j - 1], // Insert
dp[i - 1][j], // Remove
dp[i - 1][j - 1]); // Replace
}
}
return dp[m][n];
}
// Driver program
int main()
{
// your code goes here
string str1 = "sunday" ;
string str2 = "saturday" ;
cout << editDistDP(str1, str2, str1.length(), str2.length());
return 0;
}Java
// A Dynamic Programming based Java program to find minimum
// number operations to convert str1 to str2
class EDIST {
static int min( int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDistDP(String str1, String str2, int m, int n)
{
// Create a table to store results of subproblems
int dp[][] = new int [m + 1 ][n + 1 ];
// Fill d[][] in bottom up manner
for ( int i = 0 ; i <= m; i++) {
for ( int j = 0 ; j <= n; j++) {
// If first string is empty, only option is to
// insert all characters of second string
if (i == 0 )
dp[i][j] = j; // Min. operations = j
// If second string is empty, only option is to
// remove all characters of second string
else if (j == 0 )
dp[i][j] = i; // Min. operations = i
// If last characters are same, ignore last char
// and recur for remaining string
else if (str1.charAt(i - 1 ) == str2.charAt(j - 1 ))
dp[i][j] = dp[i - 1 ][j - 1 ];
// If the last character is different, consider all
// possibilities and find the minimum
else
dp[i][j] = 1 + min(dp[i][j - 1 ], // Insert
dp[i - 1 ][j], // Remove
dp[i - 1 ][j - 1 ]); // Replace
}
}
return dp[m][n];
}
public static void main(String args[])
{
String str1 = "sunday" ;
String str2 = "saturday" ;
System.out.println(editDistDP(str1, str2, str1.length(), str2.length()));
}
} /*This code is contributed by Rajat Mishra*/python
# A Dynamic Programming based Python program for edit
# distance problem
def editDistDP(str1, str2, m, n):
# Create a table to store results of subproblems
dp = [[ 0 for x in range (n + 1 )] for x in range (m + 1 )]
# Fill d[][] in bottom up manner
for i in range (m + 1 ):
for j in range (n + 1 ):
# If first string is empty, only option is to
# insert all characters of second string
if i = = 0 :
dp[i][j] = j # Min. operations = j
# If second string is empty, only option is to
# remove all characters of second string
elif j = = 0 :
dp[i][j] = i # Min. operations = i
# If last characters are same, ignore last char
# and recur for remaining string
elif str1[i - 1 ] = = str2[j - 1 ]:
dp[i][j] = dp[i - 1 ][j - 1 ]
# If last character are different, consider all
# possibilities and find minimum
else :
dp[i][j] = 1 + min (dp[i][j - 1 ], # Insert
dp[i - 1 ][j], # Remove
dp[i - 1 ][j - 1 ]) # Replace
return dp[m][n]
# Driver program
str1 = "sunday"
str2 = "saturday"
print (editDistDP(str1, str2, len (str1), len (str2)))
# This code is contributed by Bhavya JainC#
// A Dynamic Programming based
// C# program to find minimum
// number operations to
// convert str1 to str2
using System;
class GFG {
static int min( int x, int y, int z)
{
if (x <= y && x <= z)
return x;
if (y <= x && y <= z)
return y;
else
return z;
}
static int editDistDP(String str1, String str2, int m, int n)
{
// Create a table to store
// results of subproblems
int [, ] dp = new int [m + 1, n + 1];
// Fill d[][] in bottom up manner
for ( int i = 0; i <= m; i++) {
for ( int j = 0; j <= n; j++) {
// If first string is empty, only option is to
// insert all characters of second string
if (i == 0)
// Min. operations = j
dp[i, j] = j;
// If second string is empty, only option is to
// remove all characters of second string
else if (j == 0)
// Min. operations = i
dp[i, j] = i;
// If last characters are same, ignore last char
// and recur for remaining string
else if (str1[i - 1] == str2[j - 1])
dp[i, j] = dp[i - 1, j - 1];
// If the last character is different, consider all
// possibilities and find the minimum
else
dp[i, j] = 1 + min(dp[i, j - 1], // Insert
dp[i - 1, j], // Remove
dp[i - 1, j - 1]); // Replace
}
}
return dp[m, n];
}
// Driver code
public static void Main()
{
String str1 = "sunday" ;
String str2 = "saturday" ;
Console.Write(editDistDP(str1, str2, str1.Length, str2.Length));
}
}
// This Code is Contributed by Sam007PHP
<?php
// A Dynamic Programming based
// Python program for edit
// distance problem
function editDistDP( $str1 , $str2 , $m , $n )
{
// Fill d[][] in bottom up manner
for ( $i = 0; $i <= $m ; $i ++)
{
for ( $j = 0; $j <= $n ; $j ++)
{
// If first string is empty, // only option is to insert
// all characters of second string
if ( $i == 0)
$dp [ $i ][ $j ] = $j ; // Min. operations = j
// If second string is empty, // only option is to remove
// all characters of second string
else if ( $j == 0)
$dp [ $i ][ $j ] = $i ; // Min. operations = i
// If last characters are same, // ignore last char and recur
// for remaining string
else if ( $str1 [ $i - 1] == $str2 [ $j - 1])
$dp [ $i ][ $j ] = $dp [ $i - 1][ $j - 1];
// If last character are different, // consider all possibilities and
// find minimum
else
{
$dp [ $i ][ $j ] = 1 + min( $dp [ $i ][ $j - 1], // Insert
$dp [ $i - 1][ $j ], // Remove
$dp [ $i - 1][ $j - 1]); // Replace
}
}
}
return $dp [ $m ][ $n ] ;
}
// Driver Code
$str1 = "sunday" ;
$str2 = "saturday" ;
echo editDistDP( $str1 , $str2 , strlen ( $str1 ), strlen ( $str2 ));
// This code is contributed
// by Shivi_Aggarwal
?>输出如下:
3时间复杂度:O(m x n)
辅助空间:O(m x n)
复杂空间解决方案:在上述方法中, 我们需要O(m x n)空间。如果字符串的长度大于2000, 这将不合适, 因为它只能创建2000 x 2000的2D数组。要填充DP数组中的一行, 我们只需要在上一行中添加一行。例如, 如果要在DP数组中填充i = 10行, 则仅需要第9行的值。因此, 我们只需创建一个长度为2 x str1的DP数组。这种方法降低了空间复杂度。这是上述问题的C++实现。
// A Space efficient Dynamic Programming
// based C++ program to find minimum
// number operations to convert str1 to str2
#include <bits/stdc++.h>
using namespace std;
void EditDistDP(string str1, string str2)
{
int len1 = str1.length();
int len2 = str2.length();
// Create a DP array to memoize result
// of previous computations
int DP[2][len1 + 1];
// To fill the DP array with 0
memset (DP, 0, sizeof DP);
// Base condition when second string
// is empty then we remove all characters
for ( int i = 0; i <= len1; i++)
DP[0][i] = i;
// Start filling the DP
// This loop run for every
// character in second string
for ( int i = 1; i <= len2; i++) {
// This loop compares the char from
// second string with first string
// characters
for ( int j = 0; j <= len1; j++) {
// if first string is empty then
// we have to perform add character
// operation to get second string
if (j == 0)
DP[i % 2][j] = i;
// if character from both string
// is same then we do not perform any
// operation . here i % 2 is for bound
// the row number.
else if (str1[j - 1] == str2[i - 1]) {
DP[i % 2][j] = DP[(i - 1) % 2][j - 1];
}
// if character from both string is
// not same then we take the minimum
// from three specified operation
else {
DP[i % 2][j] = 1 + min(DP[(i - 1) % 2][j], min(DP[i % 2][j - 1], DP[(i - 1) % 2][j - 1]));
}
}
}
// after complete fill the DP array
// if the len2 is even then we end
// up in the 0th row else we end up
// in the 1th row so we take len2 % 2
// to get row
cout << DP[len2 % 2][len1] << endl;
}
// Driver program
int main()
{
string str1 = "food" ;
string str2 = "money" ;
EditDistDP(str1, str2);
return 0;
}输出如下:
4时间复杂度:O(m x n)
辅助空间:O(m)
应用领域:编辑距离算法有很多实际应用, 请参考Lucene示例API。另一个示例, 显示词典中与给定单词拼写错误的单词接近的所有单词。
感谢Vivek Kumar建议更新。
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请发表评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)