如何实现树遍历？先序、中序和后序遍历详细代码

2021年3月31日18:36:23 发表评论 1,242 次浏览

本文概述

与只有一种逻辑方式遍历线性数据结构(数组, 链表, 队列, 栈等)的树不同, 可以以不同的方式遍历树。以下是遍历树的常用方法。

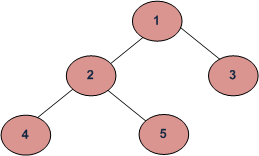
树tree示例

树示例

深度优先遍历：

(a)先序遍历(左, 根, 右)：4 2 5 1 3

(b)中序遍历(根, 左, 右)：1 2 4 5 3

(c)后续遍历(左, 右, 根)：4 5 2 3 1

广度优先或级别顺序遍历：1 2 3 4 5

请参阅这篇文章了解广度优先遍历。

先序遍历(实践)：

Algorithm Inorder(tree)
   1. Traverse the left subtree, i.e., call Inorder(left-subtree)
   2. Visit the root.
   3. Traverse the right subtree, i.e., call Inorder(right-subtree)

中序遍历的使用

对于二叉搜索树(BST)， 中序遍历以非递减的顺序给出节点。为了以非递增的顺序获取BST节点，可以使用中序遍历的一种变体，即中序遍历的反转。

示例：上面给出的数字的顺序遍历为4 2 5 1 3。

先序遍历：

Algorithm Preorder(tree)
   1. Visit the root.
   2. Traverse the left subtree, i.e., call Preorder(left-subtree)
   3. Traverse the right subtree, i.e., call Preorder(right-subtree)

先序遍历的用法

先序遍历遍历用于创建树的副本。先序遍历还用于在表达式树上获取前缀表达式。请参阅：http://en.wikipedia.org/wiki/Polish_notation了解为什么前缀表达式有用。

示例：上图给定的遍历为1 2 4 5 3。

后序遍历

Algorithm Postorder(tree)
   1. Traverse the left subtree, i.e., call Postorder(left-subtree)
   2. Traverse the right subtree, i.e., call Postorder(right-subtree)
   3. Visit the root.

后序遍历

后序遍历用于删除树。请参阅删除树的问题

有关详细信息。后序遍历对于获取表达式树的后缀表达式也很有用。请参阅http://en.wikipedia.org/wiki/Reverse_Polish_notation了解后缀表达式的用法。

示例：上图给定的事后遍历为4 5 2 3 1。

C++

// C program for different tree traversals
#include <iostream>
using namespace std;
  
/* A binary tree node has data, pointer to left child
and a pointer to right child */
struct Node
{
     int data;
     struct Node* left, *right;
     Node( int data)
     {
         this ->data = data;
         left = right = NULL;
     }
};
  
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder( struct Node* node)
{
     if (node == NULL)
         return ;
  
     // first recur on left subtree
     printPostorder(node->left);
  
     // then recur on right subtree
     printPostorder(node->right);
  
     // now deal with the node
     cout << node->data << " " ;
}
  
/* Given a binary tree, print its nodes in inorder*/
void printInorder( struct Node* node)
{
     if (node == NULL)
         return ;
  
     /* first recur on left child */
     printInorder(node->left);
  
     /* then print the data of node */
     cout << node->data << " " ;
  
     /* now recur on right child */
     printInorder(node->right);
}
  
/* Given a binary tree, print its nodes in preorder*/
void printPreorder( struct Node* node)
{
     if (node == NULL)
         return ;
  
     /* first print data of node */
     cout << node->data << " " ;
  
     /* then recur on left sutree */
     printPreorder(node->left); 
  
     /* now recur on right subtree */
     printPreorder(node->right);
} 
  
/* Driver program to test above functions*/
int main()
{
     struct Node *root = new Node(1);
     root->left             = new Node(2);
     root->right         = new Node(3);
     root->left->left     = new Node(4);
     root->left->right = new Node(5); 
  
     cout << "\nPreorder traversal of binary tree is \n" ;
     printPreorder(root);
  
     cout << "\nInorder traversal of binary tree is \n" ;
     printInorder(root); 
  
     cout << "\nPostorder traversal of binary tree is \n" ;
     printPostorder(root);
  
     return 0;
}

C

// C program for different tree traversals
#include <stdio.h>
#include <stdlib.h>
  
/* A binary tree node has data, pointer to left child
    and a pointer to right child */
struct node
{
      int data;
      struct node* left;
      struct node* right;
};
  
/* Helper function that allocates a new node with the
    given data and NULL left and right pointers. */
struct node* newNode( int data)
{
      struct node* node = ( struct node*)
                                   malloc ( sizeof ( struct node));
      node->data = data;
      node->left = NULL;
      node->right = NULL;
  
      return (node);
}
  
/* Given a binary tree, print its nodes according to the
   "bottom-up" postorder traversal. */
void printPostorder( struct node* node)
{
      if (node == NULL)
         return ;
  
      // first recur on left subtree
      printPostorder(node->left);
  
      // then recur on right subtree
      printPostorder(node->right);
  
      // now deal with the node
      printf ( "%d " , node->data);
}
  
/* Given a binary tree, print its nodes in inorder*/
void printInorder( struct node* node)
{
      if (node == NULL)
           return ;
  
      /* first recur on left child */
      printInorder(node->left);
  
      /* then print the data of node */
      printf ( "%d " , node->data);  
  
      /* now recur on right child */
      printInorder(node->right);
}
  
/* Given a binary tree, print its nodes in preorder*/
void printPreorder( struct node* node)
{
      if (node == NULL)
           return ;
  
      /* first print data of node */
      printf ( "%d " , node->data);  
  
      /* then recur on left sutree */
      printPreorder(node->left);  
  
      /* now recur on right subtree */
      printPreorder(node->right);
}    
  
/* Driver program to test above functions*/
int main()
{
      struct node *root  = newNode(1);
      root->left             = newNode(2);
      root->right           = newNode(3);
      root->left->left     = newNode(4);
      root->left->right   = newNode(5); 
  
      printf ( "\nPreorder traversal of binary tree is \n" );
      printPreorder(root);
  
      printf ( "\nInorder traversal of binary tree is \n" );
      printInorder(root);  
  
      printf ( "\nPostorder traversal of binary tree is \n" );
      printPostorder(root);
  
      getchar ();
      return 0;
}

python

# Python program to for tree traversals
  
# A class that represents an individual node in a
# Binary Tree
class Node:
     def __init__( self , key):
         self .left = None
         self .right = None
         self .val = key
  
  
# A function to do inorder tree traversal
def printInorder(root):
  
     if root:
  
         # First recur on left child
         printInorder(root.left)
  
         # then print the data of node
         print (root.val), # now recur on right child
         printInorder(root.right)
  
  
  
# A function to do postorder tree traversal
def printPostorder(root):
  
     if root:
  
         # First recur on left child
         printPostorder(root.left)
  
         # the recur on right child
         printPostorder(root.right)
  
         # now print the data of node
         print (root.val), # A function to do preorder tree traversal
def printPreorder(root):
  
     if root:
  
         # First print the data of node
         print (root.val), # Then recur on left child
         printPreorder(root.left)
  
         # Finally recur on right child
         printPreorder(root.right)
  
  
# Driver code
root = Node( 1 )
root.left      = Node( 2 )
root.right     = Node( 3 )
root.left.left  = Node( 4 )
root.left.right  = Node( 5 )
print "Preorder traversal of binary tree is"
printPreorder(root)
  
print "\nInorder traversal of binary tree is"
printInorder(root)
  
print "\nPostorder traversal of binary tree is"
printPostorder(root)

Java

// Java program for different tree traversals
  
/* Class containing left and right child of current
    node and key value*/
class Node
{
     int key;
     Node left, right;
  
     public Node( int item)
     {
         key = item;
         left = right = null ;
     }
}
  
class BinaryTree
{
     // Root of Binary Tree
     Node root;
  
     BinaryTree()
     {
         root = null ;
     }
  
     /* Given a binary tree, print its nodes according to the
       "bottom-up" postorder traversal. */
     void printPostorder(Node node)
     {
         if (node == null )
             return ;
  
         // first recur on left subtree
         printPostorder(node.left);
  
         // then recur on right subtree
         printPostorder(node.right);
  
         // now deal with the node
         System.out.print(node.key + " " );
     }
  
     /* Given a binary tree, print its nodes in inorder*/
     void printInorder(Node node)
     {
         if (node == null )
             return ;
  
         /* first recur on left child */
         printInorder(node.left);
  
         /* then print the data of node */
         System.out.print(node.key + " " );
  
         /* now recur on right child */
         printInorder(node.right);
     }
  
     /* Given a binary tree, print its nodes in preorder*/
     void printPreorder(Node node)
     {
         if (node == null )
             return ;
  
         /* first print data of node */
         System.out.print(node.key + " " );
  
         /* then recur on left sutree */
         printPreorder(node.left);
  
         /* now recur on right subtree */
         printPreorder(node.right);
     }
  
     // Wrappers over above recursive functions
     void printPostorder()  {     printPostorder(root);  }
     void printInorder()    {     printInorder(root);   }
     void printPreorder()   {     printPreorder(root);  }
  
     // Driver method
     public static void main(String[] args)
     {
         BinaryTree tree = new BinaryTree();
         tree.root = new Node( 1 );
         tree.root.left = new Node( 2 );
         tree.root.right = new Node( 3 );
         tree.root.left.left = new Node( 4 );
         tree.root.left.right = new Node( 5 );
  
         System.out.println( "Preorder traversal of binary tree is " );
         tree.printPreorder();
  
         System.out.println( "\nInorder traversal of binary tree is " );
         tree.printInorder();
  
         System.out.println( "\nPostorder traversal of binary tree is " );
         tree.printPostorder();
     }
}

C#

// C# program for different 
// tree traversals
using System; 
  
/* Class containing left and 
right child of current
node and key value*/
class Node
{
     public int key;
     public Node left, right;
  
     public Node( int item)
     {
         key = item;
         left = right = null ;
     }
}
  
class BinaryTree
{
// Root of Binary Tree
Node root;
  
BinaryTree()
{
     root = null ;
}
  
/* Given a binary tree, print 
    its nodes according to the
    "bottom-up" postorder traversal. */
void printPostorder(Node node)
{
     if (node == null )
         return ;
  
     // first recur on left subtree
     printPostorder(node.left);
  
     // then recur on right subtree
     printPostorder(node.right);
  
     // now deal with the node
     Console.Write(node.key + " " );
}
  
/* Given a binary tree, print 
    its nodes in inorder*/
void printInorder(Node node)
{
     if (node == null )
         return ;
  
     /* first recur on left child */
     printInorder(node.left);
  
     /* then print the data of node */
     Console.Write(node.key + " " );
  
     /* now recur on right child */
     printInorder(node.right);
}
  
/* Given a binary tree, print
    its nodes in preorder*/
void printPreorder(Node node)
{
     if (node == null )
         return ;
  
     /* first print data of node */
     Console.Write(node.key + " " );
  
     /* then recur on left sutree */
     printPreorder(node.left);
  
     /* now recur on right subtree */
     printPreorder(node.right);
}
  
// Wrappers over above recursive functions
void printPostorder() {printPostorder(root);}
void printInorder()  {printInorder(root);}
void printPreorder() {printPreorder(root);}
  
// Driver Code
static public void Main(String []args)
{
     BinaryTree tree = new BinaryTree();
     tree.root = new Node(1);
     tree.root.left = new Node(2);
     tree.root.right = new Node(3);
     tree.root.left.left = new Node(4);
     tree.root.left.right = new Node(5);
  
     Console.WriteLine( "Preorder traversal " + 
                        "of binary tree is " );
     tree.printPreorder();
  
     Console.WriteLine( "\nInorder traversal " +  
                         "of binary tree is " );
     tree.printInorder();
  
     Console.WriteLine( "\nPostorder traversal " + 
                           "of binary tree is " );
     tree.printPostorder();
}
}
  
// This code is contributed by Arnab Kundu

输出如下：

Preorder traversal of binary tree is
1 2 4 5 3 
Inorder traversal of binary tree is
4 2 5 1 3 
Postorder traversal of binary tree is
4 5 2 3 1

再举一个例子：

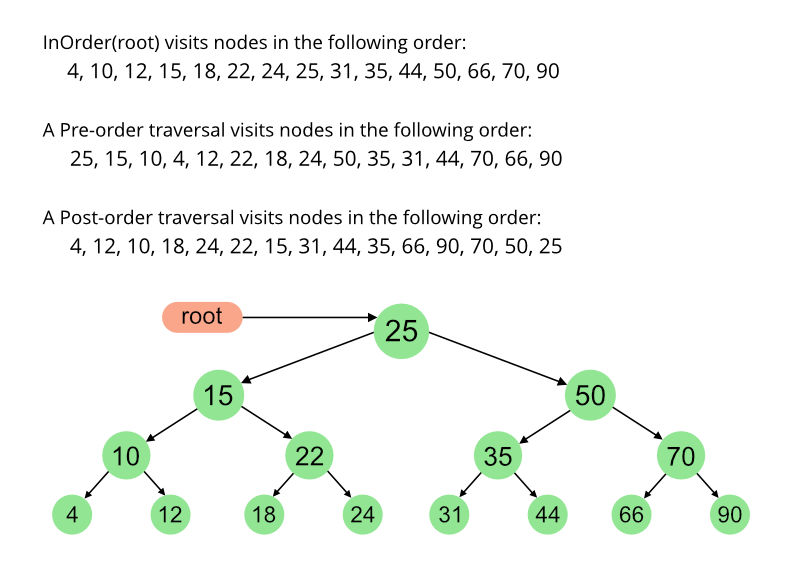
如何实现树遍历？先序、中序和后序遍历详细代码

时间复杂度：O(n)

让我们看看不同的极端情况。

对于涉及树遍历的所有问题, 复杂度函数T(n)可以定义为：

T(n)= T(k)+ T(n – k – 1)+ c

其中k是根的一侧上的节点数, 而n-k-1在另一侧上。

让我们来分析边界条件

情况1：倾斜的树(子树之一为空, 其他子树为非空)

在这种情况下, k为0。

T(n)= T(0)+ T(n-1)+ c

T(n)= 2T(0)+ T(n-2)+ 2c

T(n)= 3T(0)+ T(n-3)+ 3c

T(n)= 4T(0)+ T(n-4)+ 4c

…………………………………………

…………………………………………。

T(n)=(n-1)T(0)+ T(1)+(n-1)c

T(n)= nT(0)+(n)c

T(0)的值将是一个常数, 例如d。 (遍历一棵空树将花费一些常量时间)

T(n)= n(c + d)

T(n)=Θ(n)(n的θ)

情况2：左右子树的节点数相等。

T(n)= 2T(| _n / 2_ |)+ c

对于主方法, 此递归函数为标准形式(T(n)= aT(n / b)+(-)(n))http://en.wikipedia.org/wiki/Master_theorem。如果我们通过主方法解决它, 我们得到(-)(n)

辅助空间：如果我们不考虑函数调用的栈大小, 则为O(1)否则为O(n)。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: