怎么实现堆排序？详细解析和代码实现

2021年3月31日13:24:36 发表评论 869 次浏览

本文概述

堆排序是基于二叉堆数据结构的基于比较的排序技术。它类似于选择排序, 在这里我们首先找到最大元素, 然后将最大元素放在最后。我们对其余元素重复相同的过程。

什么是二叉堆？?

让我们首先定义一个完整的二叉树。完整的二叉树是一个二叉树, 其中除最后一个级别外, 每个级别都已完全填充, 并且所有节点都尽可能地靠左(来源维基百科：http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)

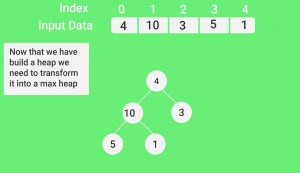
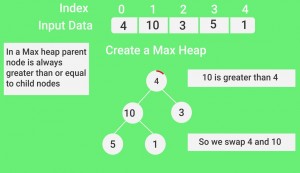
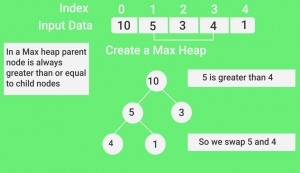
一种二叉堆是一个完整的二叉树, 其中项以特殊顺序存储, 使得父节点中的值大于(或小于)其两个子节点中的值。前者称为最大堆, 后者称为最小堆。堆可以由二叉树或数组表示。

为什么要基于数组表示二叉堆？

由于Binary Heap是完整的Binary Tree, 因此可以很容易地将其表示为数组, 并且基于数组的表示节省空间。如果父节点存储在索引I处, 则可以通过2 * I + 1来计算左子节点, 通过2 * I + 2来计算右子节点(假设索引从0开始)。

用于按升序排序的堆排序算法：

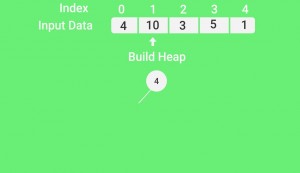
1. 根据输入数据构建最大堆。

2. 此时, 最大的项目存储在堆的根目录中。将其替换为堆的最后一项, 然后将堆的大小减小1。最后, 堆放树的根。

3. 堆大小大于1时, 请重复步骤2。

如何构建堆？

只有在堆满了其子节点后, 堆过程才能应用于该节点。因此, 必须按自下而上的顺序执行堆化。

让我们借助示例来理解：

Input data: 4, 10, 3, 5, 1
         4(0)
        /   \
     10(1)   3(2)
    /   \
 5(3)    1(4)

The numbers in bracket represent the indices in the array 
representation of data.

Applying heapify procedure to index 1:
         4(0)
        /   \
    10(1)    3(2)
    /   \
5(3)    1(4)

Applying heapify procedure to index 0:
        10(0)
        /  \
     5(1)  3(2)
    /   \
 4(3)    1(4)
The heapify procedure calls itself recursively to build heap
 in top down manner.

C++

// C++ program for implementation of Heap Sort
#include <iostream>
  
using namespace std;
  
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
void heapify( int arr[], int n, int i)
{
     int largest = i; // Initialize largest as root
     int l = 2*i + 1; // left = 2*i + 1
     int r = 2*i + 2; // right = 2*i + 2
  
     // If left child is larger than root
     if (l < n && arr[l] > arr[largest])
         largest = l;
  
     // If right child is larger than largest so far
     if (r < n && arr[r] > arr[largest])
         largest = r;
  
     // If largest is not root
     if (largest != i)
     {
         swap(arr[i], arr[largest]);
  
         // Recursively heapify the affected sub-tree
         heapify(arr, n, largest);
     }
}
  
// main function to do heap sort
void heapSort( int arr[], int n)
{
     // Build heap (rearrange array)
     for ( int i = n / 2 - 1; i >= 0; i--)
         heapify(arr, n, i);
  
     // One by one extract an element from heap
     for ( int i=n-1; i>0; i--)
     {
         // Move current root to end
         swap(arr[0], arr[i]);
  
         // call max heapify on the reduced heap
         heapify(arr, i, 0);
     }
}
  
/* A utility function to print array of size n */
void printArray( int arr[], int n)
{
     for ( int i=0; i<n; ++i)
         cout << arr[i] << " " ;
     cout << "\n" ;
}
  
// Driver program
int main()
{
     int arr[] = {12, 11, 13, 5, 6, 7};
     int n = sizeof (arr)/ sizeof (arr[0]);
  
     heapSort(arr, n);
  
     cout << "Sorted array is \n" ;
     printArray(arr, n);
}

Java

// Java program for implementation of Heap Sort
public class HeapSort
{
     public void sort( int arr[])
     {
         int n = arr.length;
  
         // Build heap (rearrange array)
         for ( int i = n / 2 - 1 ; i >= 0 ; i--)
             heapify(arr, n, i);
  
         // One by one extract an element from heap
         for ( int i=n- 1 ; i> 0 ; i--)
         {
             // Move current root to end
             int temp = arr[ 0 ];
             arr[ 0 ] = arr[i];
             arr[i] = temp;
  
             // call max heapify on the reduced heap
             heapify(arr, i, 0 );
         }
     }
  
     // To heapify a subtree rooted with node i which is
     // an index in arr[]. n is size of heap
     void heapify( int arr[], int n, int i)
     {
         int largest = i; // Initialize largest as root
         int l = 2 *i + 1 ; // left = 2*i + 1
         int r = 2 *i + 2 ; // right = 2*i + 2
  
         // If left child is larger than root
         if (l < n && arr[l] > arr[largest])
             largest = l;
  
         // If right child is larger than largest so far
         if (r < n && arr[r] > arr[largest])
             largest = r;
  
         // If largest is not root
         if (largest != i)
         {
             int swap = arr[i];
             arr[i] = arr[largest];
             arr[largest] = swap;
  
             // Recursively heapify the affected sub-tree
             heapify(arr, n, largest);
         }
     }
  
     /* A utility function to print array of size n */
     static void printArray( int arr[])
     {
         int n = arr.length;
         for ( int i= 0 ; i<n; ++i)
             System.out.print(arr[i]+ " " );
         System.out.println();
     }
  
     // Driver program
     public static void main(String args[])
     {
         int arr[] = { 12 , 11 , 13 , 5 , 6 , 7 };
         int n = arr.length;
  
         HeapSort ob = new HeapSort();
         ob.sort(arr);
  
         System.out.println( "Sorted array is" );
         printArray(arr);
     }
}

python

# Python program for implementation of heap Sort
  
# To heapify subtree rooted at index i.
# n is size of heap
def heapify(arr, n, i):
     largest = i # Initialize largest as root
     l = 2 * i + 1     # left = 2*i + 1
     r = 2 * i + 2     # right = 2*i + 2
  
     # See if left child of root exists and is
     # greater than root
     if l < n and arr[i] < arr[l]:
         largest = l
  
     # See if right child of root exists and is
     # greater than root
     if r < n and arr[largest] < arr[r]:
         largest = r
  
     # Change root, if needed
     if largest ! = i:
         arr[i], arr[largest] = arr[largest], arr[i] # swap
  
         # Heapify the root.
         heapify(arr, n, largest)
  
# The main function to sort an array of given size
def heapSort(arr):
     n = len (arr)
  
     # Build a maxheap.
     for i in range (n / / 2 - 1 , - 1 , - 1 ):
         heapify(arr, n, i)
  
     # One by one extract elements
     for i in range (n - 1 , 0 , - 1 ):
         arr[i], arr[ 0 ] = arr[ 0 ], arr[i] # swap
         heapify(arr, i, 0 )
  
# Driver code to test above
arr = [ 12 , 11 , 13 , 5 , 6 , 7 ]
heapSort(arr)
n = len (arr)
print ( "Sorted array is" )
for i in range (n):
     print ( "%d" % arr[i]), # This code is contributed by Mohit Kumra

C#

// C# program for implementation of Heap Sort
using System;
  
public class HeapSort
{
     public void sort( int [] arr)
     {
         int n = arr.Length;
  
         // Build heap (rearrange array)
         for ( int i = n / 2 - 1; i >= 0; i--)
             heapify(arr, n, i);
  
         // One by one extract an element from heap
         for ( int i=n-1; i>0; i--)
         {
             // Move current root to end
             int temp = arr[0];
             arr[0] = arr[i];
             arr[i] = temp;
  
             // call max heapify on the reduced heap
             heapify(arr, i, 0);
         }
     }
  
     // To heapify a subtree rooted with node i which is
     // an index in arr[]. n is size of heap
     void heapify( int [] arr, int n, int i)
     {
         int largest = i; // Initialize largest as root
         int l = 2*i + 1; // left = 2*i + 1
         int r = 2*i + 2; // right = 2*i + 2
  
         // If left child is larger than root
         if (l < n && arr[l] > arr[largest])
             largest = l;
  
         // If right child is larger than largest so far
         if (r < n && arr[r] > arr[largest])
             largest = r;
  
         // If largest is not root
         if (largest != i)
         {
             int swap = arr[i];
             arr[i] = arr[largest];
             arr[largest] = swap;
  
             // Recursively heapify the affected sub-tree
             heapify(arr, n, largest);
         }
     }
  
     /* A utility function to print array of size n */
     static void printArray( int [] arr)
     {
         int n = arr.Length;
         for ( int i=0; i<n; ++i)
             Console.Write(arr[i]+ " " );
         Console.Read();
     }
  
     // Driver program
     public static void Main()
     {
         int [] arr = {12, 11, 13, 5, 6, 7};
         int n = arr.Length;
  
         HeapSort ob = new HeapSort();
         ob.sort(arr);
  
         Console.WriteLine( "Sorted array is" );
         printArray(arr);
     }
}
  
// This code is contributed 
// by Akanksha Rai(Abby_akku)

PHP

<?php
  
// Php program for implementation of Heap Sort
  
// To heapify a subtree rooted with node i which is
// an index in arr[]. n is size of heap
function heapify(& $arr , $n , $i )
{
     $largest = $i ; // Initialize largest as root
     $l = 2* $i + 1; // left = 2*i + 1
     $r = 2* $i + 2; // right = 2*i + 2
  
     // If left child is larger than root
     if ( $l < $n && $arr [ $l ] > $arr [ $largest ])
         $largest = $l ;
  
     // If right child is larger than largest so far
     if ( $r < $n && $arr [ $r ] > $arr [ $largest ])
         $largest = $r ;
  
     // If largest is not root
     if ( $largest != $i )
     {
         $swap = $arr [ $i ];
         $arr [ $i ] = $arr [ $largest ];
         $arr [ $largest ] = $swap ;
  
         // Recursively heapify the affected sub-tree
         heapify( $arr , $n , $largest );
     }
}
  
// main function to do heap sort
function heapSort(& $arr , $n )
{
     // Build heap (rearrange array)
     for ( $i = $n / 2 - 1; $i >= 0; $i --)
         heapify( $arr , $n , $i );
  
     // One by one extract an element from heap
     for ( $i = $n -1; $i > 0; $i --)
     {
         // Move current root to end
         $temp = $arr [0];
             $arr [0] = $arr [ $i ];
             $arr [ $i ] = $temp ;
  
         // call max heapify on the reduced heap
         heapify( $arr , $i , 0);
     }
}
  
/* A utility function to print array of size n */
function printArray(& $arr , $n )
{
     for ( $i = 0; $i < $n ; ++ $i )
         echo ( $arr [ $i ]. " " ) ; 
          
} 
  
// Driver program
     $arr = array (12, 11, 13, 5, 6, 7);
     $n = sizeof( $arr )/sizeof( $arr [0]);
  
     heapSort( $arr , $n );
  
     echo 'Sorted array is ' . "\n" ;
      
     printArray( $arr , $n );
  
// This code is contributed by Shivi_Aggarwal
?>

输出如下：

Sorted array is
5 6 7 11 12 13

这里是以前的C代码供参考。

注意：

堆排序是一种就地算法。

它的典型实现方式不稳定, 但是可以使其稳定(参考lsin这篇文章)

时间复杂度：heapify的时间复杂度为O(Logn)。 createAndBuildHeap()的时间复杂度为O(n), 堆排序的整体时间复杂度为O(nLogn)。

HeapSort的应用

1.对几乎排序(或K排序)的数组进行排序

2.数组中的k个最大(或最小)元素

堆排序算法的用途有限, 因为Quicksort和Mergesort在实践中更好。但是, 堆数据结构本身已被大量使用。看到堆数据结构的应用

堆排序图解：

堆排序
堆排序
堆排序
堆排序
堆排序
堆排序

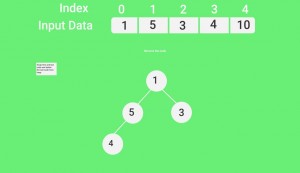
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: