算法：计算数组中的反转(逆序)S1（使用合并排序）

2021年3月30日12:45:49 发表评论 1,432 次浏览

本文概述

C ++
C
Java
Python3
C#
的PHP
C ++
C
Java
Python3
C#

数组的反转计数指示了数组距离被排序有多远(或多近)。如果数组已经排序，则反转计数为0，但如果数组是以相反的顺序排序，则反转计数为最大值。

形式上讲, 如果a [i]> a [j]且i <j, 则两个元素a [i]和a [j]构成一个求逆

例子：

Input: arr[] = {8, 4, 2, 1}
Output: 6

Explanation: Given array has six inversions:
(8, 4), (4, 2), (8, 2), (8, 1), (4, 1), (2, 1).


Input: arr[] = {3, 1, 2}
Output: 2

Explanation: Given array has two inversions:
(3, 1), (3, 2)

方法1(简单)

方法：遍历数组, 并为每个索引找到数组右侧较小元素的数量。这可以使用嵌套循环来完成。对数组中所有索引的计数求和, 然后打印总和。
算法：
1. 从头到尾遍历数组
2. 对于每个元素, 使用另一个循环查找小于当前数量的元素数, 直到该索引为止。
3. 总结每个索引的反转计数。
4. 打印反转计数。
实现

C ++

// C++ program to Count Inversions
// in an array
#include <bits/stdc++.h>
using namespace std;
 
int getInvCount( int arr[], int n)
{
     int inv_count = 0;
     for ( int i = 0; i < n - 1; i++)
         for ( int j = i + 1; j < n; j++)
             if (arr[i] > arr[j])
                 inv_count++;
 
     return inv_count;
}
 
// Driver Code
int main()
{
     int arr[] = { 1, 20, 6, 4, 5 };
     int n = sizeof (arr) / sizeof (arr[0]);
     cout << " Number of inversions are "
          << getInvCount(arr, n);
     return 0;
}
 
// This code is contributed
// by Akanksha Rai

C

// C program to Count
// Inversions in an array
#include <stdio.h>
#include <stdlib.h>
int getInvCount( int arr[], int n)
{
     int inv_count = 0;
     for ( int i = 0; i < n - 1; i++)
         for ( int j = i + 1; j < n; j++)
             if (arr[i] > arr[j])
                 inv_count++;
 
     return inv_count;
}
 
/* Driver program to test above functions */
int main()
{
     int arr[] = { 1, 20, 6, 4, 5 };
     int n = sizeof (arr) / sizeof (arr[0]);
     printf ( " Number of inversions are %d \n" , getInvCount(arr, n));
     return 0;
}

Java

// Java program to count
// inversions in an array
class Test {
     static int arr[] = new int [] { 1 , 20 , 6 , 4 , 5 };
 
     static int getInvCount( int n)
     {
         int inv_count = 0 ;
         for ( int i = 0 ; i < n - 1 ; i++)
             for ( int j = i + 1 ; j < n; j++)
                 if (arr[i] > arr[j])
                     inv_count++;
 
         return inv_count;
     }
 
     // Driver method to test the above function
     public static void main(String[] args)
     {
         System.out.println( "Number of inversions are "
                            + getInvCount(arr.length));
     }
}

Python3

# Python3 program to count
# inversions in an array
 
def getInvCount(arr, n):
 
     inv_count = 0
     for i in range (n):
         for j in range (i + 1 , n):
             if (arr[i] > arr[j]):
                 inv_count + = 1
 
     return inv_count
 
# Driver Code
arr = [ 1 , 20 , 6 , 4 , 5 ]
n = len (arr)
print ( "Number of inversions are" , getInvCount(arr, n))
 
# This code is contributed by Smitha Dinesh Semwal

C#

// C# program to count inversions
// in an array
using System;
using System.Collections.Generic;
 
class GFG {
 
     static int [] arr = new int [] { 1, 20, 6, 4, 5 };
 
     static int getInvCount( int n)
     {
         int inv_count = 0;
 
         for ( int i = 0; i < n - 1; i++)
             for ( int j = i + 1; j < n; j++)
                 if (arr[i] > arr[j])
                     inv_count++;
 
         return inv_count;
     }
 
     // Driver code
     public static void Main()
     {
         Console.WriteLine( "Number of "
                           + "inversions are "
                           + getInvCount(arr.Length));
     }
}
 
// This code is contributed by Sam007

的PHP

<?php
// PHP program to Count Inversions
// in an array
 
function getInvCount(& $arr , $n )
{
     $inv_count = 0;
     for ( $i = 0; $i < $n - 1; $i ++)
         for ( $j = $i + 1; $j < $n ; $j ++)
             if ( $arr [ $i ] > $arr [ $j ])
                 $inv_count ++;
 
     return $inv_count ;
}
 
// Driver Code
$arr = array (1, 20, 6, 4, 5 );
$n = sizeof( $arr );
echo "Number of inversions are " , getInvCount( $arr , $n );
 
// This code is contributed by ita_c
?>

输出如下：

Number of inversions are 5

复杂度分析：
- 时间复杂度：O(n ^ 2), 需要两个嵌套循环才能从头到尾遍历数组, 因此时间复杂度为O(n ^ 2)
- 空间复杂:O(1), 不需要额外的空间。

方法2(增强合并排序)

方法：
假设数组左半边和右半边的反转次数(分别为inv1和inv2), 在Inv1 + Inv2中没有考虑哪些反转？答案是–在合并步骤中需要计算的反转数。因此, 要获得许多反转, 需要在左子数组, 右子数组和merge()中添加许多反转。

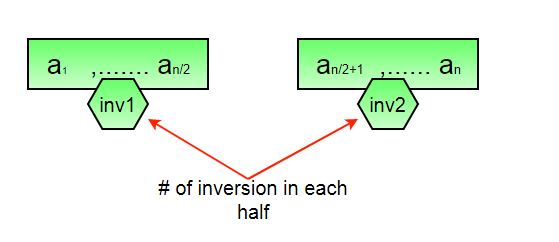
怎么获得的merge()中的反转次数？
在合并过程中, 让我用于索引左子数组, 让j用于右子数组。在merge()的任何步骤中, 如果a [i]大于a [j], 则存在(mid – i)个反转。因为左子数组和右子数组已排序, 所以左子数组中的所有其余元素(a [i + 1], a [i + 2]…a [mid])将大于a [j]

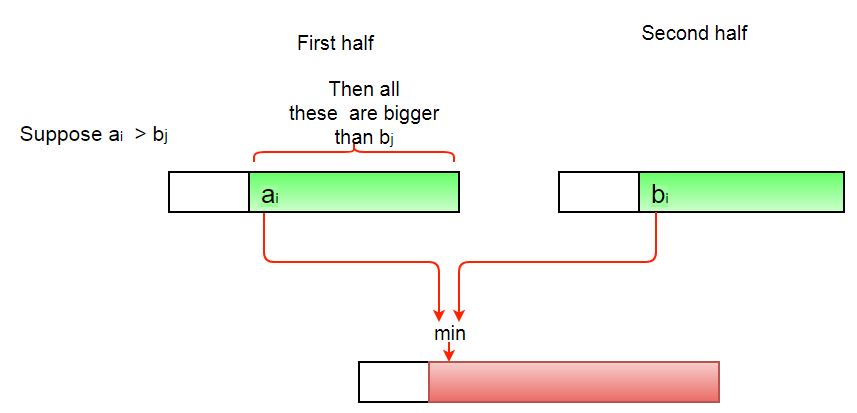
完整图片：

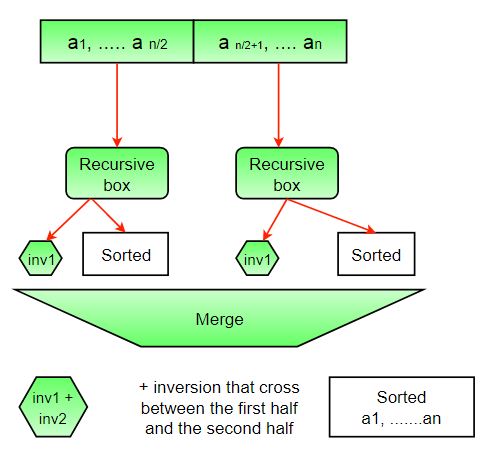
算法：
1. 这个想法类似于合并排序, 将数组分成两个相等或几乎相等的两半, 直到达到基本情况为止。
2. 创建一个函数合并, 计算合并数组的两半时的反转次数, 创建两个索引i和j, i是上半部分的索引, j是下半部分的索引。如果a [i]大于a [j], 则存在(mid – i)个反演。因为左子数组和右子数组已排序, 所以左子数组中的所有其余元素(a [i + 1], a [i + 2]…a [mid])将大于a [j]。
3. 创建一个递归函数, 将数组分成两半, 然后求和前一半的求反数, 再求后一半的求反数, 然后将二者合并, 求出答案。
4. 递归的基本情况是在给定的一半中只有一个元素。
5. 打印答案
实现

C ++

// C++ program to Count
// Inversions in an array
// using Merge Sort
#include <bits/stdc++.h>
using namespace std;
 
int _mergeSort( int arr[], int temp[], int left, int right);
int merge( int arr[], int temp[], int left, int mid, int right);
 
/* This function sorts the
    input array and returns the
number of inversions in the array */
int mergeSort( int arr[], int array_size)
{
     int temp[array_size];
     return _mergeSort(arr, temp, 0, array_size - 1);
}
 
/* An auxiliary recursive function
   that sorts the input array and
returns the number of inversions in the array. */
int _mergeSort( int arr[], int temp[], int left, int right)
{
     int mid, inv_count = 0;
     if (right > left) {
         /* Divide the array into two parts and
         call _mergeSortAndCountInv()
         for each of the parts */
         mid = (right + left) / 2;
 
         /* Inversion count will be sum of
         inversions in left-part, right-part
         and number of inversions in merging */
         inv_count += _mergeSort(arr, temp, left, mid);
         inv_count += _mergeSort(arr, temp, mid + 1, right);
 
         /*Merge the two parts*/
         inv_count += merge(arr, temp, left, mid + 1, right);
     }
     return inv_count;
}
 
/* This funt merges two sorted arrays
and returns inversion count in the arrays.*/
int merge( int arr[], int temp[], int left, int mid, int right)
{
     int i, j, k;
     int inv_count = 0;
 
     i = left; /* i is index for left subarray*/
     j = mid; /* j is index for right subarray*/
     k = left; /* k is index for resultant merged subarray*/
     while ((i <= mid - 1) && (j <= right)) {
         if (arr[i] <= arr[j]) {
             temp[k++] = arr[i++];
         }
         else {
             temp[k++] = arr[j++];
 
             /* this is tricky -- see above
             explanation/diagram for merge()*/
             inv_count = inv_count + (mid - i);
         }
     }
 
     /* Copy the remaining elements of left subarray
(if there are any) to temp*/
     while (i <= mid - 1)
         temp[k++] = arr[i++];
 
     /* Copy the remaining elements of right subarray
(if there are any) to temp*/
     while (j <= right)
         temp[k++] = arr[j++];
 
     /*Copy back the merged elements to original array*/
     for (i = left; i <= right; i++)
         arr[i] = temp[i];
 
     return inv_count;
}
 
// Driver code
int main()
{
     int arr[] = { 1, 20, 6, 4, 5 };
     int n = sizeof (arr) / sizeof (arr[0]);
     int ans = mergeSort(arr, n);
     cout << " Number of inversions are " << ans;
     return 0;
}
 
// This is code is contributed by rathbhupendra

C

// C program to Count
// Inversions in an array
// using Merge Sort
#include <stdio.h>
#include <stdlib.h>
 
int _mergeSort( int arr[], int temp[], int left, int right);
int merge( int arr[], int temp[], int left, int mid, int right);
 
/* This function sorts the input array and returns the
    number of inversions in the array */
int mergeSort( int arr[], int array_size)
{
     int * temp = ( int *) malloc ( sizeof ( int ) * array_size);
     return _mergeSort(arr, temp, 0, array_size - 1);
}
 
/* An auxiliary recursive function that sorts the input
   array and returns the number of inversions in the array.
*/
int _mergeSort( int arr[], int temp[], int left, int right)
{
     int mid, inv_count = 0;
     if (right > left) {
         /* Divide the array into two parts and call
        _mergeSortAndCountInv() for each of the parts */
         mid = (right + left) / 2;
 
         /* Inversion count will be the sum of inversions in
       left-part, right-part and number of inversions in
       merging */
         inv_count += _mergeSort(arr, temp, left, mid);
         inv_count += _mergeSort(arr, temp, mid + 1, right);
 
         /*Merge the two parts*/
         inv_count += merge(arr, temp, left, mid + 1, right);
     }
     return inv_count;
}
 
/* This funt merges two sorted arrays and returns inversion
    count in the arrays.*/
int merge( int arr[], int temp[], int left, int mid, int right)
{
     int i, j, k;
     int inv_count = 0;
 
     i = left; /* i is index for left subarray*/
     j = mid; /* j is index for right subarray*/
     k = left; /* k is index for resultant merged subarray*/
     while ((i <= mid - 1) && (j <= right)) {
         if (arr[i] <= arr[j]) {
             temp[k++] = arr[i++];
         }
         else {
             temp[k++] = arr[j++];
 
             /*this is tricky -- see above
              * explanation/diagram for merge()*/
             inv_count = inv_count + (mid - i);
         }
     }
 
     /* Copy the remaining elements of left subarray
    (if there are any) to temp*/
     while (i <= mid - 1)
         temp[k++] = arr[i++];
 
     /* Copy the remaining elements of right subarray
    (if there are any) to temp*/
     while (j <= right)
         temp[k++] = arr[j++];
 
     /*Copy back the merged elements to original array*/
     for (i = left; i <= right; i++)
         arr[i] = temp[i];
 
     return inv_count;
}
 
/* Driver program to test above functions */
int main( int argv, char ** args)
{
     int arr[] = { 1, 20, 6, 4, 5 };
     printf ( " Number of inversions are %d \n" , mergeSort(arr, 5));
     getchar ();
     return 0;
}

Java

// Java implementation of the approach
import java.util.Arrays;
 
public class GFG {
 
     // Function to count the number of inversions
     // during the merge process
     private static int mergeAndCount( int [] arr, int l, int m, int r)
     {
 
         // Left subarray
         int [] left = Arrays.copyOfRange(arr, l, m + 1 );
 
         // Right subarray
         int [] right = Arrays.copyOfRange(arr, m + 1 , r + 1 );
 
         int i = 0 , j = 0 , k = l, swaps = 0 ;
 
         while (i < left.length && j < right.length)
         {
             if (left[i] <= right[j])
                 arr[k++] = left[i++];
             else {
                 arr[k++] = right[j++];
                 swaps += (m + 1 ) - (l + i);
             }
         }
         return swaps;
     }
 
     // Merge sort function
     private static int mergeSortAndCount( int [] arr, int l, int r)
     {
 
         // Keeps track of the inversion count at a
         // particular node of the recursion tree
         int count = 0 ;
 
         if (l < r) {
             int m = (l + r) / 2 ;
 
             // Total inversion count = left subarray count
             // + right subarray count + merge count
 
             // Left subarray count
             count += mergeSortAndCount(arr, l, m);
 
             // Right subarray count
             count += mergeSortAndCount(arr, m + 1 , r);
 
             // Merge count
             count += mergeAndCount(arr, l, m, r);
         }
 
         return count;
     }
 
     // Driver code
     public static void main(String[] args)
     {
         int [] arr = { 1 , 20 , 6 , 4 , 5 };
 
         System.out.println(mergeSortAndCount(arr, 0 , arr.length - 1 ));
     }
}
 
// This code is contributed by Pradip Basak

Python3

# Python 3 program to count inversions in an array
 
# Function to Use Inversion Count
def mergeSort(arr, n):
     # A temp_arr is created to store
     # sorted array in merge function
     temp_arr = [ 0 ] * n
     return _mergeSort(arr, temp_arr, 0 , n - 1 )
 
# This Function will use MergeSort to count inversions
 
def _mergeSort(arr, temp_arr, left, right):
 
     # A variable inv_count is used to store
     # inversion counts in each recursive call
 
     inv_count = 0
 
     # We will make a recursive call if and only if
     # we have more than one elements
 
     if left < right:
 
         # mid is calculated to divide the array into two subarrays
         # Floor division is must in case of python
 
         mid = (left + right) / / 2
 
         # It will calculate inversion
         # counts in the left subarray
 
         inv_count + = _mergeSort(arr, temp_arr, left, mid)
 
         # It will calculate inversion
         # counts in right subarray
 
         inv_count + = _mergeSort(arr, temp_arr, mid + 1 , right)
 
         # It will merge two subarrays in
         # a sorted subarray
 
         inv_count + = merge(arr, temp_arr, left, mid, right)
     return inv_count
 
# This function will merge two subarrays
# in a single sorted subarray
def merge(arr, temp_arr, left, mid, right):
     i = left     # Starting index of left subarray
     j = mid + 1 # Starting index of right subarray
     k = left     # Starting index of to be sorted subarray
     inv_count = 0
 
     # Conditions are checked to make sure that
     # i and j don't exceed their
     # subarray limits.
 
     while i < = mid and j < = right:
 
         # There will be no inversion if arr[i] <= arr[j]
 
         if arr[i] < = arr[j]:
             temp_arr[k] = arr[i]
             k + = 1
             i + = 1
         else :
             # Inversion will occur.
             temp_arr[k] = arr[j]
             inv_count + = (mid - i + 1 )
             k + = 1
             j + = 1
 
     # Copy the remaining elements of left
     # subarray into temporary array
     while i < = mid:
         temp_arr[k] = arr[i]
         k + = 1
         i + = 1
 
     # Copy the remaining elements of right
     # subarray into temporary array
     while j < = right:
         temp_arr[k] = arr[j]
         k + = 1
         j + = 1
 
     # Copy the sorted subarray into Original array
     for loop_var in range (left, right + 1 ):
         arr[loop_var] = temp_arr[loop_var]
         
     return inv_count
 
# Driver Code
# Given array is
arr = [ 1 , 20 , 6 , 4 , 5 ]
n = len (arr)
result = mergeSort(arr, n)
print ( "Number of inversions are" , result)
 
# This code is contributed by ankush_953

C#

// C# implementation of counting the
// inversion using merge sort
 
using System;
public class Test {
 
     /* This method sorts the input array and returns the
        number of inversions in the array */
     static int mergeSort( int [] arr, int array_size)
     {
         int [] temp = new int [array_size];
         return _mergeSort(arr, temp, 0, array_size - 1);
     }
 
     /* An auxiliary recursive method that sorts the input
       array and returns the number of inversions in the
       array. */
     static int _mergeSort( int [] arr, int [] temp, int left, int right)
     {
         int mid, inv_count = 0;
         if (right > left) {
             /* Divide the array into two parts and call
            _mergeSortAndCountInv() for each of the parts */
             mid = (right + left) / 2;
 
             /* Inversion count will be the sum of inversions
           in left-part, right-part
           and number of inversions in merging */
             inv_count += _mergeSort(arr, temp, left, mid);
             inv_count
                 += _mergeSort(arr, temp, mid + 1, right);
 
             /*Merge the two parts*/
             inv_count
                 += merge(arr, temp, left, mid + 1, right);
         }
         return inv_count;
     }
 
     /* This method merges two sorted arrays and returns
        inversion count in the arrays.*/
     static int merge( int [] arr, int [] temp, int left, int mid, int right)
     {
         int i, j, k;
         int inv_count = 0;
 
         i = left; /* i is index for left subarray*/
         j = mid; /* j is index for right subarray*/
         k = left; /* k is index for resultant merged
                      subarray*/
         while ((i <= mid - 1) && (j <= right)) {
             if (arr[i] <= arr[j]) {
                 temp[k++] = arr[i++];
             }
             else {
                 temp[k++] = arr[j++];
 
                 /*this is tricky -- see above
                  * explanation/diagram for merge()*/
                 inv_count = inv_count + (mid - i);
             }
         }
 
         /* Copy the remaining elements of left subarray
        (if there are any) to temp*/
         while (i <= mid - 1)
             temp[k++] = arr[i++];
 
         /* Copy the remaining elements of right subarray
        (if there are any) to temp*/
         while (j <= right)
             temp[k++] = arr[j++];
 
         /*Copy back the merged elements to original array*/
         for (i = left; i <= right; i++)
             arr[i] = temp[i];
 
         return inv_count;
     }
 
     // Driver method to test the above function
     public static void Main()
     {
         int [] arr = new int [] { 1, 20, 6, 4, 5 };
         Console.Write( "Number of inversions are "
                       + mergeSort(arr, 5));
     }
}
// This code is contributed by Rajput-Ji

输出如下：

Number of inversions are 5

复杂度分析：
- 时间复杂度：O(n log n), 使用的算法是分治法, 因此在每个级别中需要一个完整的数组遍历, 并且存在log n个级别, 因此时间复杂度为O(n log n)。
- 空间复杂:O(n), 临时数组。

请注意, 上面的代码修改(或排序)了输入数组。如果我们只想计算倒数, 那么我们需要创建一个原始数组的副本, 并在副本上调用mergeSort()。

计算数组中的反转设置2(使用自平衡BST)

使用C++ STL中的Set计数反转

计算数组中的反转第三组(使用BIT)

参考文献：

http://www.cs.umd.edu/class/fall2009/cmsc451/lectures/Lec08-inversions.pdf

http://www.cp.eng.chula.ac.th/~piak/teaching/algo/algo2008/count-inv.htm

如果你在上述程序/算法或其他解决相同问题的方法中发现任何错误, 请发表评论。

本文概述

C ++

C

Java

Python3

C#

的PHP

C ++

C

Java

Python3

C#

发表评论取消回复

登录 注册 找回密码

登录注册找回密码