算法：使用步数1、2或3计算到达第n个楼梯的所有方式

2021年3月29日16:37:07 发表评论 950 次浏览

一个孩子正在n步的楼梯上奔跑, 可以一次跳1步, 2步或3步。实现一种方法来计算孩子可以上楼梯的可能方式。

例子：

Input : 4
Output : 7
Explantion:
Below are the four ways
 1 step + 1 step + 1 step + 1 step
 1 step + 2 step + 1 step
 2 step + 1 step + 1 step 
 1 step + 1 step + 2 step
 2 step + 2 step
 3 step + 1 step
 1 step + 3 step

Input : 3
Output : 4
Explantion:
Below are the four ways
 1 step + 1 step + 1 step
 1 step + 2 step
 2 step + 1 step
 3 step

有两种方法可以解决此问题：

  1. 递归方法
  2. 动态规划

方法1：递归。

有n个楼梯, 允许一个人跳下一个楼梯, 跳过一个楼梯或跳过两个楼梯。因此, 这里有n个楼梯。因此, 如果某人站在第i楼梯, 则该人可以移至第i + 1, i + 2, i + 3楼梯。可以形成一个递归函数, 其中在当前索引i处递归调用第i + 1, i + 2和i + 3个楼梯。

还有另一种形成递归函数的方法。要到达楼梯i, 一个人必须从i-1, i-2或i-3楼梯上跳下, 或者我是起始楼梯。

算法：

  1. 创建一个仅包含一个参数的递归函数(count(int n))。
  2. 检查基本情况。如果n的值小于0, 则返回0；如果n的值等于0, 则返回1, 因为它是起始楼梯。
  3. 用值n-1, n-2和n-3递归调用函数并求和返回的值, 即sum = count(n-1)+ count(n-2)+ count(n-3)
  4. 返回总和的值。

C ++

// C++ Program to find n-th stair using step size
// 1 or 2 or 3.
#include <iostream>
using namespace std;
  
class GFG {
  
     // Returns count of ways to reach n-th stair
     // using 1 or 2 or 3 steps.
public :
     int findStep( int n)
     {
         if (n == 1 || n == 0)
             return 1;
         else if (n == 2)
             return 2;
  
         else
             return findStep(n - 3) + findStep(n - 2)
                                    + findStep(n - 1);
     }
};
  
// Driver code
int main()
{
     GFG g;
     int n = 4;
     cout << g.findStep(n);
     return 0;
}
  
// This code is contributed by SoM15242

C

// Program to find n-th stair using step size
// 1 or 2 or 3.
#include <stdio.h>
  
// Returns count of ways to reach n-th stair
// using 1 or 2 or 3 steps.
int findStep( int n)
{
     if (n == 1 || n == 0)
         return 1;
     else if (n == 2)
         return 2;
  
     else
         return findStep(n - 3) + findStep(n - 2) + findStep(n - 1);
}
  
// Driver code
int main()
{
     int n = 4;
     printf ( "%d\n" , findStep(n));
     return 0;
}

Java

// Program to find n-th stair
// using step size 1 or 2 or 3.
import java.util.*;
import java.lang.*;
  
public class GfG {
  
     // Returns count of ways to reach
     // n-th stair using 1 or 2 or 3 steps.
     public static int findStep( int n)
     {
         if (n == 1 || n == 0 )
             return 1 ;
         else if (n == 2 )
             return 2 ;
  
         else
             return findStep(n - 3 ) + findStep(n - 2 ) + findStep(n - 1 );
     }
  
     // Driver function
     public static void main(String argc[])
     {
         int n = 4 ;
         System.out.println(findStep(n));
     }
}
  
/* This code is contributed by Sagar Shukla */

python

# Python program to find n-th stair  
# using step size 1 or 2 or 3.
  
# Returns count of ways to reach n-th 
# stair using 1 or 2 or 3 steps.
def findStep( n) :
     if (n = = 1 or n = = 0 ) :
         return 1
     elif (n = = 2 ) :
         return 2
      
     else :
         return findStep(n - 3 ) + findStep(n - 2 ) + findStep(n - 1 ) 
  
  
# Driver code
n = 4
print (findStep(n))
  
# This code is contributed by Nikita Tiwari.

C#

// Program to find n-th stair
// using step size 1 or 2 or 3.
using System;
  
public class GfG {
  
     // Returns count of ways to reach
     // n-th stair using 1 or 2 or 3 steps.
     public static int findStep( int n)
     {
         if (n == 1 || n == 0)
             return 1;
         else if (n == 2)
             return 2;
  
         else
             return findStep(n - 3) + findStep(n - 2) + findStep(n - 1);
     }
  
     // Driver function
     public static void Main()
     {
         int n = 4;
         Console.WriteLine(findStep(n));
     }
}
  
/* This code is contributed by vt_m */

的PHP

<?php
// PHP Program to find n-th stair 
// using step size 1 or 2 or 3.
  
// Returns count of ways to 
// reach n-th stair using  
// 1 or 2 or 3 steps.
function findStep( $n )
{
     if ( $n == 1 || $n == 0) 
         return 1;
     else if ( $n == 2) 
         return 2;
      
     else
         return findStep( $n - 3) + 
                findStep( $n - 2) +
                 findStep( $n - 1); 
}
  
// Driver code
$n = 4;
echo findStep( $n );
  
// This code is contributed by m_kit
?>

输出：

7

工作图解：

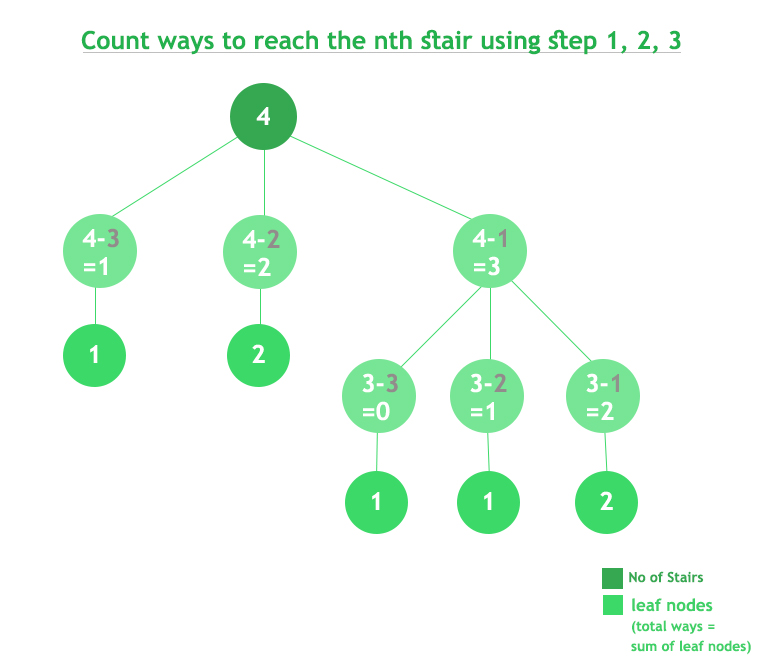
使用步数1、2或3计算到达第n个楼梯的方式1

复杂度分析：

  • 时间复杂度：O(3^n)。
    上述解决方案的时间复杂度是指数的, 一个接近的上限为O(3^n)。从每个状态, 调用3个递归函数。所以n个状态的上限是O(3^n)。
  • 空间复杂度：O(1)。
    由于不需要额外的空间。

注意：可以使用动态规划来优化程序的时间复杂度。

方法2:动态规划。

这个想法是相似的, 但是可以观察到有n个状态, 但是递归函数被称为3 ^ n次。这意味着某些状态会被反复调用。因此, 想法是存储状态值。这可以通过两种方式完成。

  • 自上而下的方法：第一种方法是保持递归结构完整, 仅将值存储在HashMap中, 每当再次调用该函数时, 都将返回值存储而不进行计算()。
  • 自下而上的方法：第二种方法是占用n大小的额外空间, 并开始计算从1、2 ..到n的状态值, 即计算i, i + 1, i + 2的值, 然后使用它们来计算i的值+3。

算法：

  1. 创建一个大小为n + 1的数组, 并使用1、1、2(基本情况)初始化前三个变量。
  2. 从3循环到n。
  3. 对于每个索引i, 第i个位置的计算机值分别为dp [i] = dp [i-1] + dp [i-2] + dp [i-3]。
  4. 打印dp [n]的值, 作为达到第n步的方式的计数。

C ++

// A C++ program to count number of ways
// to reach n't stair when
#include <iostream>
using namespace std;
  
// A recursive function used by countWays
int countWays( int n)
{
     int res[n + 1];
     res[0] = 1;
     res[1] = 1;
     res[2] = 2;
     for ( int i = 3; i <= n; i++)
         res[i] = res[i - 1] + res[i - 2]
                 + res[i - 3];
  
     return res[n];
}
  
// Driver program to test above functions
int main()
{
     int n = 4;
     cout << countWays(n);
     return 0;
}
//This code is contributed by shubhamsingh10

C

// A C program to count number of ways
// to reach n't stair when
#include <stdio.h>
  
// A recursive function used by countWays
int countWays( int n)
{
     int res[n + 1];
     res[0] = 1;
     res[1] = 1;
     res[2] = 2;
     for ( int i = 3; i <= n; i++)
         res[i] = res[i - 1] + res[i - 2]
                  + res[i - 3];
  
     return res[n];
}
  
// Driver program to test above functions
int main()
{
     int n = 4;
     printf ( "%d" , countWays(n));
     return 0;
}

Java

// Program to find n-th stair
// using step size 1 or 2 or 3.
import java.util.*;
import java.lang.*;
  
public class GfG {
  
     // A recursive function used by countWays
     public static int countWays( int n)
     {
         int [] res = new int [n + 1 ];
         res[ 0 ] = 1 ;
         res[ 1 ] = 1 ;
         res[ 2 ] = 2 ;
  
         for ( int i = 3 ; i <= n; i++)
             res[i] = res[i - 1 ] + res[i - 2 ]
                      + res[i - 3 ];
  
         return res[n];
     }
  
     // Driver function
     public static void main(String argc[])
     {
         int n = 4 ;
         System.out.println(countWays(n));
     }
}
  
/* This code is contributed by Sagar Shukla */

python

# Python program to find n-th stair  
# using step size 1 or 2 or 3.
  
# A recursive function used by countWays
def countWays(n) :
     res = [ 0 ] * (n + 2 )
     res[ 0 ] = 1
     res[ 1 ] = 1
     res[ 2 ] = 2
      
     for i in range ( 3 , n + 1 ) :
         res[i] = res[i - 1 ] + res[i - 2 ] + res[i - 3 ]
      
     return res[n]
  
# Driver code
n = 4
print (countWays(n))
  
  
# This code is contributed by Nikita Tiwari.

C#

// Program to find n-th stair
// using step size 1 or 2 or 3.
using System;
  
public class GfG {
  
     // A recursive function used by countWays
     public static int countWays( int n)
     {
         int [] res = new int [n + 2];
         res[0] = 1;
         res[1] = 1;
         res[2] = 2;
  
         for ( int i = 3; i <= n; i++)
             res[i] = res[i - 1] + res[i - 2]
                      + res[i - 3];
  
         return res[n];
     }
  
     // Driver function
     public static void Main()
     {
         int n = 4;
         Console.WriteLine(countWays(n));
     }
}
  
/* This code is contributed by vt_m */

的PHP

<?php
// A PHP program to count 
// number of ways to reach 
// n'th stair when
  
// A recursive function
// used by countWays
function countWays( $n )
{
     $res [0] = 1;
     $res [1] = 1;
     $res [2] = 2;
     for ( $i = 3; $i <= $n ; $i ++) 
         $res [ $i ] = $res [ $i - 1] + 
                    $res [ $i - 2] + 
                    $res [ $i - 3];
      
     return $res [ $n ];
}
  
// Driver Code
$n = 4;
echo countWays( $n );
  
// This code is contributed by ajit
?>

输出：

7

工作图解：

1 -> 1 -> 1 -> 1
1 -> 1 -> 2
1 -> 2 -> 1
1 -> 3
2 -> 1 -> 1
2 -> 2
3 -> 1

So Total ways: 7

复杂度分析：

  • 时间复杂度：O(n)。
    只需遍历数组。因此, 时间复杂度为O(n)。
  • 空间复杂度：O(n)。
    要将值存储在DP中, 需要n个额外的空间。

如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: