本文概述
以下是的常见定义二项式系数.
二项式系数C(n, k)可定义为(1 + x)^n展开后x^k的系数。二项式系数C(n, k)也给出了从n个对象中更正式地选择k个对象的方法的数量,而不考虑顺序,即n个元素集合的k个元素子集(或k个组合)的数量。问题
写一个函数,接受两个参数n和k,并返回二项式系数C(n, k)的值。例如,当n = 4和k = 2时,你的函数应该返回6,当n = 5和k = 2时,它应该返回10。
1)最优子结构
可以使用以下用于二项式系数的标准公式来递归计算C(n, k)的值。
C(n, k) = C(n-1, k-1) + C(n-1, k)
C(n, 0) = C(n, n) = 1以下是一个简单的递归实现, 它仅遵循上述递归结构。
C ++
// A naive recursive C++ implementation
#include <bits/stdc++.h>
using namespace std;
// Returns value of Binomial Coefficient C(n, k)
int binomialCoeff( int n, int k)
{
// Base Cases
if (k == 0 || k == n)
return 1;
// Recur
return binomialCoeff(n - 1, k - 1) +
binomialCoeff(n - 1, k);
}
/* Driver code*/
int main()
{
int n = 5, k = 2;
cout << "Value of C(" <<n<< ", " <<k<< ") is " <<
binomialCoeff(n, k);
return 0;
}
// This is code is contributed by rathbhupendraC
// A Naive Recursive Implementation
#include<stdio.h>
// Returns value of Binomial Coefficient C(n, k)
int binomialCoeff( int n, int k)
{
// Base Cases
if (k==0 || k==n)
return 1;
// Recur
return binomialCoeff(n-1, k-1) +
binomialCoeff(n-1, k);
}
/* Driver program to test above function*/
int main()
{
int n = 5, k = 2;
printf ( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k));
return 0;
}Java
// JAVA Code for Dynamic Programming |
// Set 9 (Binomial Coefficient)
import java.util.*;
class GFG {
// Returns value of Binomial
// Coefficient C(n, k)
static int binomialCoeff( int n, int k)
{
// Base Cases
if (k == 0 || k == n)
return 1 ;
// Recur
return binomialCoeff(n - 1 , k - 1 ) +
binomialCoeff(n - 1 , k);
}
/* Driver program to test above function */
public static void main(String[] args)
{
int n = 5 , k = 2 ;
System.out.printf( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k));
}
}
// This code is contributed by Arnav Kr. Mandal.python
# A naive recursive Python implementation
def binomialCoeff(n , k):
if k = = 0 or k = = n :
return 1
# Recursive Call
return binomialCoeff(n - 1 , k - 1 ) +
binomialCoeff(n - 1 , k)
# Driver Program to test ht above function
n = 5
k = 2
print "Value of C(%d, %d) is (%d)" % (n , k , binomialCoeff(n , k))
# This code is contributed by Nikhil Kumar Singh (nickzuck_007)C#
// C# Code for Dynamic Programming |
// Set 9 (Binomial Coefficient)
using System;
class GFG {
// Returns value of Binomial
// Coefficient C(n, k)
static int binomialCoeff( int n, int k)
{
// Base Cases
if (k == 0 || k == n)
return 1;
// Recur
return binomialCoeff(n - 1, k - 1) +
binomialCoeff(n - 1, k);
}
/* Driver program to test above function */
public static void Main()
{
int n = 5, k = 2;
Console.Write( "Value of C(" + n + ", "
+ k + ") is " +
binomialCoeff(n, k));
}
}
// This code is contributed by Sam007.的PHP
<?php
// PHP Code for Dynamic Programming |
// Set 9 (Binomial Coefficient)
// Returns value of
// Binomial Coefficient C(n, k)
function binomialCoeff( $n , $k )
{
// Base Cases
if ( $k ==0 || $k == $n )
return 1;
// Recur
return binomialCoeff( $n - 1, $k - 1) +
binomialCoeff( $n - 1, $k );
}
// Driver Code
$n = 5;
$k = 2;
echo "Value of C" , "(" , $n , $k , ") is "
, binomialCoeff( $n , $k );
// This code is contributed by aj_36
?>输出如下
Value of C(5, 2) is 102)重叠子问题
应该注意的是, 上述函数一次又一次地计算相同的子问题。有关n = 5和k = 2, 请参见下面的递归树。函数C(3, 1)被调用两次。对于较大的n值, 将存在许多常见的子问题。
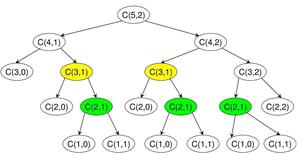
C(5, 2)的二项式系数递归树
由于再次调用了相同的子问题, 因此此问题具有"重叠子问题"属性。因此, 二项式系数问题具有两个属性(请参阅这个和这个)的动态编程问题。像其他典型的动态编程(DP)问题, 可以通过自下而上的方式构造一个临时2D数组C [] []来避免相同子问题的重新计算。以下是基于动态编程的实现。
C ++
// A Dynamic Programming based solution that uses
// table C[][] to calculate the Binomial Coefficient
#include<bits/stdc++.h>
using namespace std;
// Prototype of a utility function that
// returns minimum of two integers
int min( int a, int b);
// Returns value of Binomial Coefficient C(n, k)
int binomialCoeff( int n, int k)
{
int C[n + 1][k + 1];
int i, j;
// Caculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++)
{
for (j = 0; j <= min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using previously
// stored values
else
C[i][j] = C[i - 1][j - 1] +
C[i - 1][j];
}
}
return C[n][k];
}
// A utility function to return
// minimum of two integers
int min( int a, int b)
{
return (a < b) ? a : b;
}
// Driver Code
int main()
{
int n = 5, k = 2;
cout << "Value of C[" << n << "]["
<< k << "] is " << binomialCoeff(n, k);
}
// This code is contributed by Shivi_AggarwalC
// A Dynamic Programming based solution
// that uses table C[][] to
// calculate the Binomial Coefficient
#include<stdio.h>
// Prototype of a utility function that
// returns minimum of two integers
int min( int a, int b);
// Returns value of Binomial Coefficient C(n, k)
int binomialCoeff( int n, int k)
{
int C[n+1][k+1];
int i, j;
// Caculate value of Binomial Coefficient
// in bottom up manner
for (i = 0; i <= n; i++)
{
for (j = 0; j <= min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1;
// Calculate value using
// previously stored values
else
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
return C[n][k];
}
// A utility function to return
// minimum of two integers
int min( int a, int b)
{
return (a<b)? a: b;
}
/* Drier program to test above function*/
int main()
{
int n = 5, k = 2;
printf ( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k) );
return 0;
}Java
// A Dynamic Programming based
// solution that uses table C[][] to
// calculate the Binomial Coefficient
class BinomialCoefficient
{
// Returns value of Binomial
// Coefficient C(n, k)
static int binomialCoeff( int n, int k)
{
int C[][] = new int [n+ 1 ][k+ 1 ];
int i, j;
// Calculate value of Binomial
// Coefficient in bottom up manner
for (i = 0 ; i <= n; i++)
{
for (j = 0 ; j <= min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i][j] = 1 ;
// Calculate value using
// previously stored values
else
C[i][j] = C[i- 1 ][j- 1 ] + C[i- 1 ][j];
}
}
return C[n][k];
}
// A utility function to return
// minimum of two integers
static int min( int a, int b)
{
return (a<b)? a: b;
}
/* Driver program to test above function*/
public static void main(String args[])
{
int n = 5 , k = 2 ;
System.out.println( "Value of C(" +n+ ", " +k+ ") is " +
binomialCoeff(n, k));
}
}
/*This code is contributed by Rajat Mishra*/python
# A Dynamic Programming based Python
# Program that uses table C[][]
# to calculate the Binomial Coefficient
# Returns value of Binomial Coefficient C(n, k)
def binomialCoef(n, k):
C = [[ 0 for x in range (k + 1 )] for x in range (n + 1 )]
# Calculate value of Binomial
# Coefficient in bottom up manner
for i in range (n + 1 ):
for j in range ( min (i, k) + 1 ):
# Base Cases
if j = = 0 or j = = i:
C[i][j] = 1
# Calculate value using
# previously stored values
else :
C[i][j] = C[i - 1 ][j - 1 ] + C[i - 1 ][j]
return C[n][k]
# Driver program to test above function
n = 5
k = 2
print ( "Value of C[" + str (n) + "][" + str (k) + "] is "
+ str (binomialCoef(n, k)))
# This code is contributed by Bhavya JainC#
// A Dynamic Programming based solution that
// uses table C[][] to calculate the Binomial
// Coefficient
using System;
class GFG {
// Returns value of Binomial Coefficient
// C(n, k)
static int binomialCoeff( int n, int k)
{
int [, ]C = new int [n+1, k+1];
int i, j;
// Calculate value of Binomial
// Coefficient in bottom up manner
for (i = 0; i <= n; i++)
{
for (j = 0; j <= Math.Min(i, k); j++)
{
// Base Cases
if (j == 0 || j == i)
C[i, j] = 1;
// Calculate value using previously
// stored values
else
C[i, j] = C[i-1, j-1] + C[i-1, j];
}
}
return C[n, k];
}
// A utility function to return minimum
// of two integers
static int min( int a, int b)
{
return (a < b) ? a : b;
}
/* Driver program to test above function*/
public static void Main()
{
int n = 5, k = 2;
Console.WriteLine( "Value of C(" + n
+ ", " + k + ") is "
+ binomialCoeff(n, k));
}
}
// This code is contributed by anuj_67.的PHP
<?php
// A Dynamic Programming based
// solution that uses table C[][] to
// calculate the Binomial Coefficient
// Returns value of Binomial
// Coefficient C(n, k)
function binomialCoeff( $n , $k )
{
$C = array ( array ());
$i ; $j ;
// Caculate value of Binomial
// Coefficient in bottom up manner
for ( $i = 0; $i <= $n ; $i ++)
{
for ( $j = 0; $j <= min( $i , $k ); $j ++)
{
// Base Cases
if ( $j == 0 || $j == $i )
$C [ $i ][ $j ] = 1;
// Calculate value using
// previously stored values
else
$C [ $i ][ $j ] = $C [ $i - 1][ $j - 1] +
$C [ $i - 1][ $j ];
}
}
return $C [ $n ][ $k ];
}
// Driver Code
$n = 5;
$k = 2;
echo "Value of C(" , $n , " " , $k , ") is" , " "
, binomialCoeff( $n , $k ) ;
// This code is contributed by anuj_67.
?>输出如下
Value of C[5][2] is 10时间复杂度:O(n * k)
辅助空间:O(n * k)
下面是上述代码的空间优化版本。下面的代码只使用O(k)。感谢AK提出了这个方法。
C ++
// C++ program for space optimized Dynamic Programming
// Solution of Binomial Coefficient
#include<bits/stdc++.h>
using namespace std;
int binomialCoeff( int n, int k)
{
int C[k+1];
memset (C, 0, sizeof (C));
C[0] = 1; // nC0 is 1
for ( int i = 1; i <= n; i++)
{
// Compute next row of pascal triangle using
// the previous row
for ( int j = min(i, k); j > 0; j--)
C[j] = C[j] + C[j-1];
}
return C[k];
}
/* Drier program to test above function*/
int main()
{
int n = 5, k = 2;
printf ( "Value of C(%d, %d) is %d " , n, k, binomialCoeff(n, k) );
return 0;
}Java
// JAVA Code for Dynamic Programming |
// Set 9 (Binomial Coefficient)
import java.util.*;
class GFG {
static int binomialCoeff( int n, int k)
{
int C[] = new int [k + 1 ];
// nC0 is 1
C[ 0 ] = 1 ;
for ( int i = 1 ; i <= n; i++)
{
// Compute next row of pascal
// triangle using the previous row
for ( int j = Math.min(i, k); j > 0 ; j--)
C[j] = C[j] + C[j- 1 ];
}
return C[k];
}
/* Driver program */
public static void main(String[] args)
{
int n = 5 , k = 2 ;
System.out.printf( "Value of C(%d, %d) is %d "
, n, k, binomialCoeff(n, k));
}
}python
# Python program for Optimized
# Dynamic Programming solution to
# Binomail Coefficient. This one
# uses the concept of pascal
# Triangle and less memory
def binomialCoeff(n , k):
# Declaring an empty array
C = [ 0 for i in xrange (k + 1 )]
C[ 0 ] = 1 #since nC0 is 1
for i in range ( 1 , n + 1 ):
# Compute next row of pascal triangle using
# the previous row
j = min (i , k)
while (j> 0 ):
C[j] = C[j] + C[j - 1 ]
j - = 1
return C[k]
# Driver Program to test the above function
n = 5
k = 2
print "Value of C(%d, %d) is %d" % (n, k, binomialCoeff(n, k))
# This code is contribtued by Nikhil Kumar Singh(nickzuck_007)C#
// C# Code for Dynamic Programming |
// Set 9 (Binomial Coefficient)
using System;
class GFG {
static int binomialCoeff( int n, int k)
{
int [] C = new int [k + 1];
// nC0 is 1
C[0] = 1;
for ( int i = 1; i <= n; i++)
{
// Compute next row of pascal
// triangle using the previous
// row
for ( int j = Math.Min(i, k);
j > 0; j--)
C[j] = C[j] + C[j-1];
}
return C[k];
}
/* Driver program */
public static void Main()
{
int n = 5, k = 2;
Console.WriteLine( "Value of C("
+ n + " " + k + ") is "
+ binomialCoeff(n, k));
}
}
// This code is contribtued by anuj_67.的PHP
<?php
// PHP program for space optimized
// Dynamic Programming Solution of
// Binomial Coefficient
function binomialCoeff( $n , $k )
{
$C = array_fill (0, $k + 1, 0);
$C [0] = 1; // nC0 is 1
for ( $i = 1; $i <= $n ; $i ++)
{
// Compute next row of pascal
// triangle using the previous row
for ( $j = min( $i , $k ); $j > 0; $j --)
$C [ $j ] = $C [ $j ] + $C [ $j - 1];
}
return $C [ $k ];
}
// Driver Code
$n = 5; $k = 2;
echo "Value of C[$n, $k] is " .
binomialCoeff( $n , $k );
// This code is contributed by mits.
?>输出如下
Value of C(5, 2) is 10时间复杂度:
O(n * k)
辅助空间:O(k)
说明:
1 ========== >> >> n = 0, C(0, 0)= 1
1–1 ======== >>>> n = 1, C(1, 0)= 1, C(1, 1)= 1
1–2–1 ====== >> n = 2, C(2, 0)= 1, C(2, 1)= 2, C(2, 2)= 1
1–3–3–1 ==== >> n = 3, C(3, 0)= 1, C(3, 1)= 3, C(3, 2)= 3, C(3, 3) = 1
1–4–6–4–1 == >> n = 4, C(4, 0)= 1, C(4, 1)= 4, C(4, 2)= 6, C(4, 3) = 4, C(4, 4)= 1
因此, 这里的每个i循环都使用第(i-1)行建立第i行Pascal三角形
在任何时候, 数组C的每个元素都会有一个值(零或更大), 并且在下一次迭代中, 这些元素的值来自上一次迭代。
在表达式中,
C [j] = C [j] + C [j-1]
右侧代表来自上一迭代的值(Pascal三角形的一行取决于上一行)。左侧代表此语句将获得的当前迭代的值。
Let's say we want to calculate C(4, 3), i.e. n=4, k=3:
All elements of array C of size 4 (k+1) are
initialized to ZERO.
i.e. C[0] = C[1] = C[2] = C[3] = C[4] = 0;
Then C[0] is set to 1
For i = 1:
C[1] = C[1] + C[0] = 0 + 1 = 1 ==>> C(1, 1) = 1
For i = 2:
C[2] = C[2] + C[1] = 0 + 1 = 1 ==>> C(2, 2) = 1
C[1] = C[1] + C[0] = 1 + 1 = 2 ==>> C(2, 1) = 2
For i=3:
C[3] = C[3] + C[2] = 0 + 1 = 1 ==>> C(3, 3) = 1
C[2] = C[2] + C[1] = 1 + 2 = 3 ==>> C(3, 2) = 3
C[1] = C[1] + C[0] = 2 + 1 = 3 ==>> C(3, 1) = 3
For i=4:
C[4] = C[4] + C[3] = 0 + 1 = 1 ==>> C(4, 4) = 1
C[3] = C[3] + C[2] = 1 + 3 = 4 ==>> C(4, 3) = 4
C[2] = C[2] + C[1] = 3 + 3 = 6 ==>> C(4, 2) = 6
C[1] = C[1] + C[0] = 3 + 1 = 4 ==>> C(4, 1) = 4
C(4, 3) = 4 is would be the answer in our example.记忆方式:这个想法是创建一个查找表并遵循递归自上而下的方法。在计算任何值之前, 我们检查它是否已经在查找表中。如果是, 我们返回值。否则, 我们计算该值并将其存储在查找表中。以下是动态规划的自顶向下方法, 以查找二项式系数的值。
C ++
// A Dynamic Programming based
// solution that uses
// table dp[][] to calculate
// the Binomial Coefficient
// A naive recursive approach
// with table C++ implementation
#include <bits/stdc++.h>
using namespace std;
// Returns value of Binomial Coefficient C(n, k)
int binomialCoeffUtil( int n, int k, int ** dp)
{
// If value in lookup table then return
if (dp[n][k] != -1) //
return dp[n][k];
// store value in a table before return
if (k == 0) {
dp[n][k] = 1;
return dp[n][k];
}
// store value in table before return
if (k == n) {
dp[n][k] = 1;
return dp[n][k];
}
// save value in lookup table before return
dp[n][k] = binomialCoeffUtil(n - 1, k - 1, dp) +
binomialCoeffUtil(n - 1, k, dp);
return dp[n][k];
}
int binomialCoeff( int n, int k)
{
int ** dp; // make a temporary lookup table
dp = new int *[n + 1];
// loop to create table dynamically
for ( int i = 0; i < (n + 1); i++) {
dp[i] = new int [k + 1];
}
// nested loop to initialise the table with -1
for ( int i = 0; i < (n + 1); i++) {
for ( int j = 0; j < (k + 1); j++) {
dp[i][j] = -1;
}
}
return binomialCoeffUtil(n, k, dp);
}
/* Driver code*/
int main()
{
int n = 5, k = 2;
cout << "Value of C(" << n << ", " << k << ") is "
<< binomialCoeff(n, k) << endl;
return 0;
}
// This is code is contributed by MOHAMMAD MUDASSIRJava
// A Dynamic Programming based
// solution that uses
// table dp[][] to calculate
// the Binomial Coefficient
// A naive recursive approach
// with table Java implementation
import java.util.*;
class GFG{
// Returns value of Binomial
// Coefficient C(n, k)
static int binomialCoeffUtil( int n, int k, Vector<Integer> []dp)
{
// If value in lookup table
// then return
if (dp[n].get(k) != - 1 )
return dp[n].get(k);
// store value in a table
// before return
if (k == 0 )
{
dp[n].add(k, 1 );
return dp[n].get(k);
}
// store value in table
// before return
if (k == n)
{
dp[n].add(k, 1 );
return dp[n].get(k);
}
// save value in lookup table
// before return
dp[n].add(k, binomialCoeffUtil(n - 1 , k - 1 , dp) +
binomialCoeffUtil(n - 1 , k, dp));
return dp[n].get(k);
}
static int binomialCoeff( int n, int k)
{
// Make a temporary lookup table
Vector<Integer> []dp = new Vector[n+ 1 ];
// Loop to create table dynamically
for ( int i = 0 ; i < (n + 1 ); i++)
{
dp[i] = new Vector<Integer>();
for ( int j = 0 ; j <= k; j++)
dp[i].add(- 1 );
}
return binomialCoeffUtil(n, k, dp);
}
// Driver code
public static void main(String[] args)
{
int n = 5 , k = 2 ;
System.out.print( "Value of C(" + n +
", " + k + ") is " +
binomialCoeff(n, k) + "\n" );
}
}
// This code is contributed by Rajput-JiPython3
# A Dynamic Programming based solution
# that uses table dp[][] to calculate
# the Binomial Coefficient. A naive
# recursive approach with table
# Python3 implementation
# Returns value of Binomial
# Coefficient C(n, k)
def binomialCoeffUtil(n, k, dp):
# If value in lookup table then return
if dp[n][k] ! = - 1 :
return dp[n][k]
# Store value in a table before return
if k = = 0 :
dp[n][k] = 1
return dp[n][k]
# Store value in table before return
if k = = n:
dp[n][k] = 1
return dp[n][k]
# Save value in lookup table before return
dp[n][k] = (binomialCoeffUtil(n - 1 , k - 1 , dp) +
binomialCoeffUtil(n - 1 , k, dp))
return dp[n][k]
def binomialCoeff(n, k):
# Make a temporary lookup table
dp = [ [ - 1 for y in range (k + 1 ) ]
for x in range (n + 1 ) ]
return binomialCoeffUtil(n, k, dp)
# Driver code
n = 5
k = 2
print ( "Value of C(" + str (n) +
", " + str (k) + ") is" , binomialCoeff(n, k))
# This is code is contributed by Prateek GuptaC#
// C# program for the
// above approach
// A Dynamic Programming based
// solution that uses
// table [, ]dp to calculate
// the Binomial Coefficient
// A naive recursive approach
// with table C# implementation
using System;
using System.Collections.Generic;
class GFG{
// Returns value of Binomial
// Coefficient C(n, k)
static int binomialCoeffUtil( int n, int k, List< int > []dp)
{
// If value in lookup table
// then return
if (dp[n][k] != -1)
return dp[n][k];
// store value in a table
// before return
if (k == 0)
{
dp[n][k] = 1;
return dp[n][k];
}
// store value in table
// before return
if (k == n)
{
dp[n][k] = 1;
return dp[n][k];
}
// save value in lookup table
// before return
dp[n][k] = binomialCoeffUtil(n - 1, k - 1, dp) +
binomialCoeffUtil(n - 1, k, dp);
return dp[n][k];
}
static int binomialCoeff( int n, int k)
{
// Make a temporary lookup table
List< int > []dp = new List< int >[n + 1];
// Loop to create table dynamically
for ( int i = 0; i < (n + 1); i++)
{
dp[i] = new List< int >();
for ( int j = 0; j <= k; j++)
dp[i].Add(-1);
}
return binomialCoeffUtil(n, k, dp);
}
// Driver code
public static void Main(String[] args)
{
int n = 5, k = 2;
Console.Write( "Value of C(" + n +
", " + k + ") is " +
binomialCoeff(n, k) + "\n" );
}
}
// This code is contributed by 29AjayKumar输出如下
Value of C(5, 2) is 10参考文献:
http://www.csl.mtu.edu/cs4321/www/Lectures/Lecture%2015%20-%20Dynamic%20Programming%20Binomial%20Coefficients.htm
如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)