如何为给定的序列设计计数器？（图解）

问题-为序列设计同步计数器:0→1→3→4→5→7→0，使用T触发器。

说明–对于给定的序列, 状态转换图如下：

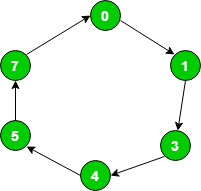
状态转换表逻辑：

当前状态	下一状态
0	1
1	3
3	4
4	5
5	7
7	0

给定序列的状态转换表：

当前状态	下一状态
Q3	Q2	Q1	Q3(t + 1)	Q2(t + 1)	Q1(t + 1)
0	0	0	0	0	1
0	0	1	0	1	1
0	1	1	1	0	0
1	0	0	1	0	1
1	0	1	1	1	1
1	1	1	0	0	0

T触发器–如果Q值从0变为1或从1变为0, 则T触发器的输入为1, 否则输入值为0。

Qt	Qt + 1	T
0	0	0
0	1	1
1	0	1
1	1	0

使用T触发器的激励表绘制所有T触发器的输入表。由于T型触发器的本质是切换。在此, Q3为最高有效位, Q1为最低有效位。

触发器输入表
T3	T2	T1
0	0	1
0	1	0
1	1	1
0	0	1
0	1	0
1	1	1

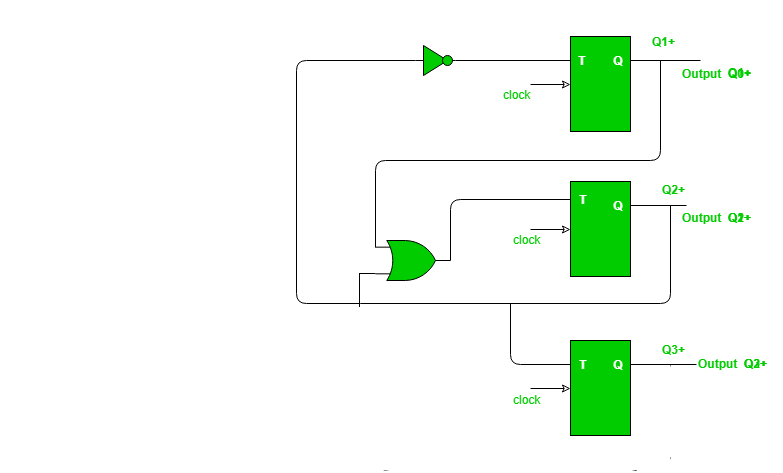
利用K-Map (Karnaugh Map)求Q3、Q2、Q1中T3、T2、T1的值:：

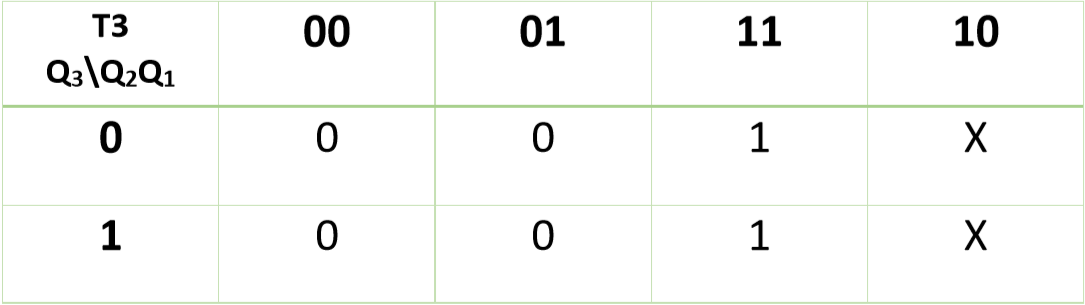
因此,

T3 = Q2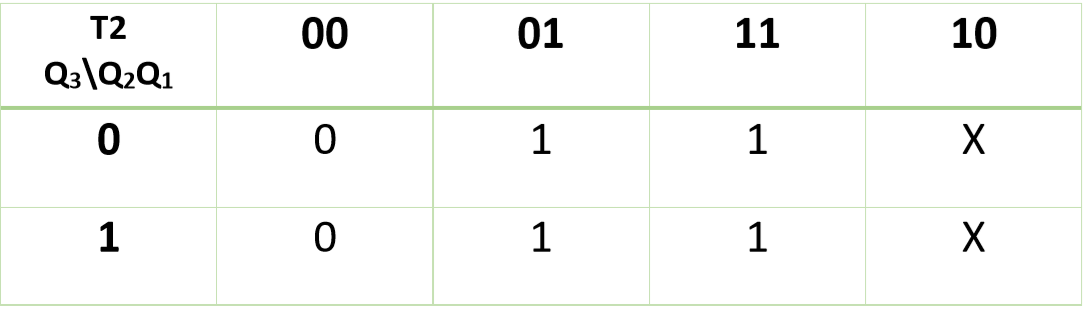

因此,

T2 = Q1 + Q2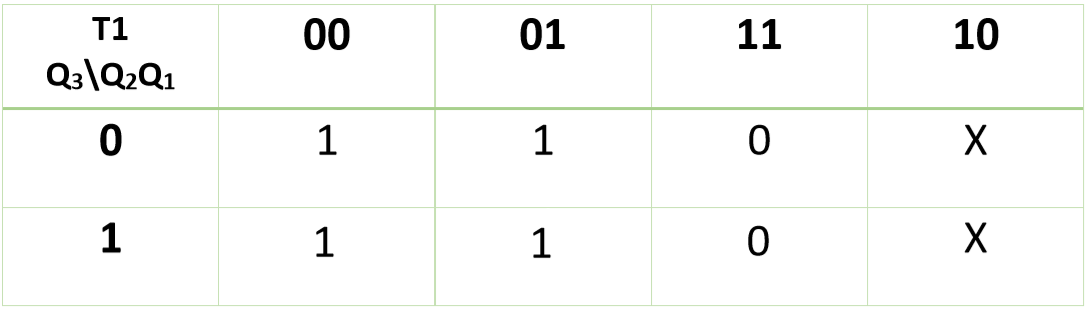

因此,

T1 = Q2’

现在, 你可以使用K-map的表达式设计所需的电路：

---