算法题：如何计算矩形中的正方形数？

2021年3月25日11:46:30 发表评论 1,224 次浏览

本文概述

给定一个m x n的矩形, 其中有多少个正方形？

例子 ：

Input:  m = 2, n = 2
Output: 5
There are 4 squares of size 1x1 + 
          1 square of size 2x2.

Input: m = 4, n = 3
Output: 20
There are 12 squares of size 1x1 + 
          6 squares of size 2x2 + 
          2 squares of size 3x3.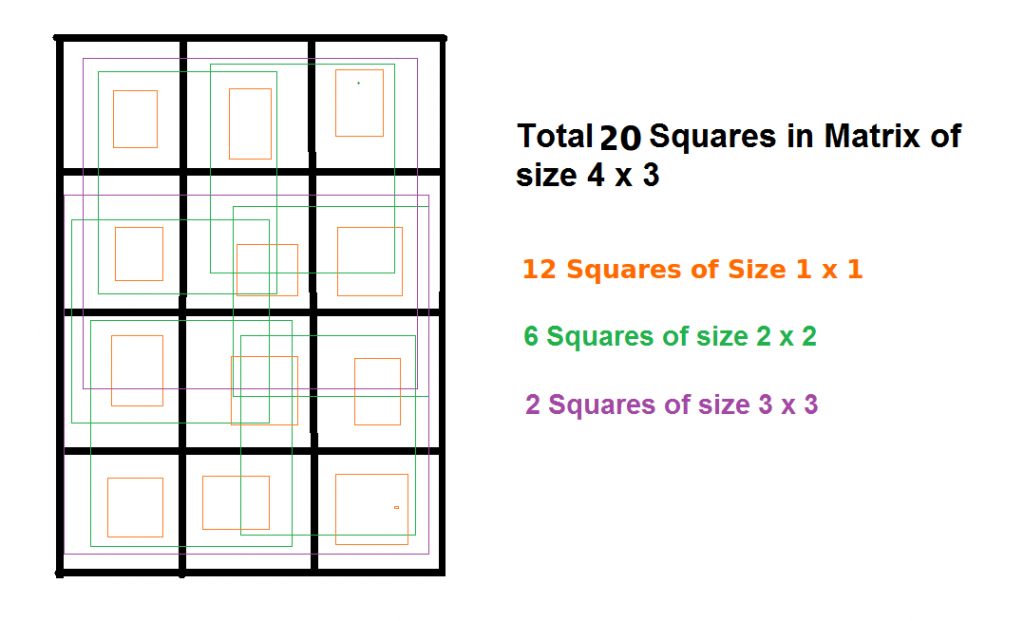
方格

推荐：请在"实践首先, 在继续解决方案之前。

让我们首先解决m = n的问题, 即正方形的问题：

对于m = n = 1, 输出：1

对于m = n = 2, 输出：4 + 1 [4的大小为1×1 + 1的大小为2×2]

对于m = n = 3, 输出：9 + 4 + 1 [4尺寸为1×1 + 4尺寸为2×2 + 1尺寸为3×3]

对于m = n = 4, 输出16 + 9 + 4 +1 [16的大小为1×1 + 9的大小为2×2 + 4的大小为3×3 + 1的大小为4×4]

通常, 它似乎是n ^ 2 +(n-1)^ 2 +…1 = n(n + 1)(2n + 1)/ 6

当m不等于n时, 让我们解决这个问题：

让我们假设m <= n

通过以上解释, 我们知道m x m矩阵中的平方数为m(m + 1)(2m + 1)/ 6

当我们添加一列时, 即m x(m + 1)矩阵中的平方数是多少？

当我们添加一列时, 增加的平方数为m +(m-1)+…+ 3 + 2 +1

[尺寸为1×1的m平方+尺寸为2×2的(m-1)平方+…+尺寸为m x m的1平方]

等于m(m + 1)/ 2

因此, 当我们添加(n-m)列时, 增加的平方总数为(n-m)* m(m + 1)/ 2。

因此, 平方总数为m(m + 1)(2m + 1)/ 6 +(n-m)* m(m + 1)/ 2。

使用相同的逻辑, 我们可以证明n <= m。

所以总的来说

Total number of squares = m x (m+1) x (2m+1)/6 + 
                          (n-m) x m x (m+1)/2 

when n is larger dimension

.

对矩形使用上述逻辑, 我们还可以证明一个正方形中的正方形数为n(n + 1)(2n + 1)/ 6

下面是上述公式的实现。

C ++

// C++ program to count squares 
// in a rectangle of size m x n
#include<iostream>
using namespace std;
  
// Returns count of all squares 
// in a rectangle of size m x n
int countSquares( int m, int n)
{
// If n is smaller, swap m and n
if (n < m)
     swap(m, n);
  
// Now n is greater dimension, // apply formula
return m * (m + 1) * (2 * m + 1) / 
      6 + (n - m) * m *(m + 1) / 2;
}
  
// Driver Code
int main()
{
int m = 4, n = 3;
cout << "Count of squares is "
      << countSquares(m, n);
}

Java

// Java program to count squares
// in a rectangle of size m x n
  
class GFG
{
     // Returns count of all squares 
     // in a rectangle of size m x n
     static int countSquares( int m, int n)
     {
     // If n is smaller, swap m and n
     if (n < m)
     {
         // swap(m, n)
         int temp = m;
         m = n;
         n = temp;
     }
          
      
     // Now n is greater dimension, // apply formula
     return m * (m + 1 ) * ( 2 * m + 1 ) / 
         6 + (n - m) * m * (m + 1 ) / 2 ;
     }
      
     // Driver Code
     public static void main(String[] args) 
     {
         int m = 4 , n = 3 ;
         System.out.println( "Count of squares is " + 
                             countSquares(m, n));
     }
}

Python3

# Python3 program to count squares
# in a rectangle of size m x n
  
# Returns count of all squares 
# in a rectangle of size m x n
def countSquares(m, n):
      
     # If n is smaller, swap m and n
     if (n < m):
         temp = m
         m = n
         n = temp
          
     # Now n is greater dimension, # apply formula
     return ((m * (m + 1 ) * ( 2 * m + 1 ) / 
            6 + (n - m) * m * (m + 1 ) / 2 ))
  
# Driver Code
if __name__ = = '__main__' :
     m = 4 
     n = 3
     print ( "Count of squares is "
          , countSquares(m, n))
  
# This code is contributed by mits.

C#

// C# program to count squares in a rectangle
// of size m x n
using System;
  
class GFG {
      
     // Returns count of all squares in a 
     // rectangle of size m x n
     static int countSquares( int m, int n)
     {
     // If n is smaller, swap m and n
     if (n < m)
     {
         // swap(m, n)
         int temp = m;
         m = n;
         n = temp;
     }
              
     // Now n is greater dimension, apply 
     // formula
     return m * (m + 1) * (2 * m + 1) / 6 + 
                (n - m) * m * (m + 1) / 2;
     }
      
     // Driver method
     public static void Main() 
     {
         int m = 4, n = 3;
          
         Console.WriteLine( "Count of squares is " 
                           + countSquares(m, n));
     }
}
  
//This code is contributed by vt_m.

的PHP

<?php
// PHP program to count squares
// in a rectangle of size m x n
  
// Returns count of all squares 
// in a rectangle of size m x n
function countSquares( $m , $n )
{
     // If n is smaller, swap m and n
     if ( $n < $m )
         list( $m , $n ) = array ( $n , $m );
      
     // Now n is greater dimension, // apply formula
     return $m * ( $m + 1) * (2 * $m + 1) / 
        6 + ( $n - $m ) * $m * ( $m + 1) / 2;
}
  
// Driver Code
$m = 4; $n = 3;
echo ( "Count of squares is " . countSquares( $m , $n ));
  
// This code is contributed by Ajit.
?>

输出：

Count of Squares is 20

替代解决方案：

让我们取m = 2, n = 3；

边1的平方数将是6, 因为将存在两种情况, 一种是沿水平(2)的1单元边的正方形, 第二种是沿垂直(3)的1单元边的正方形。给我们2 * 3 = 6平方

当边为2个单位时, 一种情况将是仅沿一个位置水平放置2个单位的边的正方形, 而第二个情况将为垂直放置两个位置的情况。所以平方数= 2

所以我们可以推断出

大小为1 * 1的平方数将为m * n

大小2 * 2的平方数将为(n-1)(m-1)

因此, 大小为n的平方数将为1 *(m-n + 1)

总平方数的最终公式为

n *(n + 1)(3m-n + 1)/ 6

C ++

// C++ program to count squares 
// in a rectangle of size m x n
#include<iostream>
using namespace std;
  
// Returns count of all squares
// in a rectangle of size m x n
int countSquares( int m, int n) 
{
  
     // If n is smaller, swap m and n
     if (n < m) 
     {
         int temp = m;
         m = n;
         n = temp;
     }
  
     // Now n is greater dimension, // apply formula
     return n * (n + 1) * (3 * m - n + 1) / 6;
}
  
// Driver Code
int main()
{
     int m = 4, n = 3;
     cout << "Count of squares is "
          << countSquares(m, n);
}
  
// This code is contributed by 29AjayKumar

Java

// Java program to count squares 
// in a rectangle of size m x n 
import java.util.*;
  
class GFG 
{
  
     // Returns count of all squares
     // in a rectangle of size m x n
     static int countSquares( int m, int n) 
     {
  
         // If n is smaller, swap m and n
         if (n < m) 
         {
             int temp = m;
             m = n;
             n = temp;
         }
  
         // Now n is greater dimension, // apply formula
         return n * (n + 1 ) * ( 3 * m - n + 1 ) / 6 ;
     }
  
     // Driver Code
     public static void main(String[] args) 
     {
         int m = 4 ;
         int n = 3 ;
         System.out.print( "Count of squares is " + 
                              countSquares(m, n));
     }
}
  
// This code is contributed by 29AjayKumar

Python3

# Python3 program to count squares 
# in a rectangle of size m x n 
  
# Returns count of all squares 
# in a rectangle of size m x n 
def countSquares(m, n): 
      
     # If n is smaller, swap m and n 
     if (n < m): 
         temp = m 
         m = n 
         n = temp 
          
     # Now n is greater dimension, # apply formula 
     return n * (n + 1 ) * ( 3 * m - n + 1 ) / / 6
  
# Driver Code 
if __name__ = = '__main__' : 
     m = 4
     n = 3
     print ( "Count of squares is" , countSquares(m, n)) 
  
# This code is contributed by AnkitRai01

C#

// C# program to count squares 
// in a rectangle of size m x n 
using System;
  
class GFG 
{
  
     // Returns count of all squares
     // in a rectangle of size m x n
     static int countSquares( int m, int n) 
     {
  
         // If n is smaller, swap m and n
         if (n < m) 
         {
             int temp = m;
             m = n;
             n = temp;
         }
  
         // Now n is greater dimension, // apply formula
         return n * (n + 1) * (3 * m - n + 1) / 6;
     }
  
     // Driver Code
     public static void Main(String[] args) 
     {
         int m = 4;
         int n = 3;
         Console.Write( "Count of squares is " + 
                           countSquares(m, n));
     }
}
  
// This code is contributed by Rajput-Ji

输出：

Count of Squares is 20

感谢Pranav提供此替代解决方案。

如果发现任何不正确的地方, 或者你想分享有关上述主题的更多信息, 请发表评论

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: