8085程序来确定数字是否为质数

问题–使用8085微处理器编写汇编语言程序, 以确定给定数字是否为质数。

如果数字是素数, 则将01H存储在存储结果的存储位置, 否则为00H。

例子：

Input : 03H
Output : 01H
The number 3 only has two divisors, 1 and 3. 
Hence, it is prime.
Input : 09H
Output : 00H
The number 9 has three divisors, 1, 3 and 9. 
Hence, it is composite.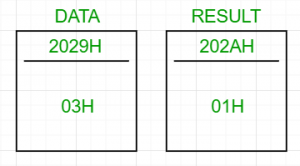

质数是只有两个除数的数, 即1和数本身。

另一方面, 一个复合数具有3个或更多的除数。

算法：

1. 以n为输入
2. 运行从i = n到1的循环。对于每次迭代, 请检查i是否将n完全除。如果是, 那么我就是n除数
3. 记录n个除数的总数
4. 如果除数的数量为2, 则该数量为质数, 否则为合成数

如何确定我是否为除数？

继续从股息中减去i, 直到股息变为0或小于0。现在, 检查股息的值。如果为0, 则我为除数, 否则为除数。

步骤如下：

1. 将数据从存储位置(2029H, 任意选择)加载到累加器中
2. 用00H初始化寄存器C。这存储n的除数
3. 将值移到E中的累加器中。这将作为循环的迭代器从n到1。
4. 将值移动到B中的累加器中。B会永久存储n, 因为累加器中的值将更改
5. 将E中的值移到D并以累加器为除数, 以D为除数进行除法。
6. 除法：继续从A中减去D, 直到A中的值变为0或小于0。之后, 检查累加器中的值。如果等于0, 则通过将C中的值加1来增加除数的数量
7. 通过将B中的值移到A来恢复累加器的值, 并继续循环直到E变为0
8. 现在, 将除数的数量从C移到A, 然后检查其是否等于2。如果是, 则将01H存储到202AH(任意), 否则存储00H。

202AH包含结果。

地址	标签	助记符
2000H		LDA 2029H
2001H
2002H
2003H		MVI C, 00H
2004H
2005H		MOV E, A
2006H		MOV B, A
2007H	循环1	MOV D, E
2008H	循环2	CMP D
2009H		JC DIVIDENDLESSTHAN0
200AH
200BH
200CH		SUB D
200DH		JNZ LOOP2
200EH
200FH
2010H	DIVIDENDLESSTHAN0	CPI 00H
2011H
2012H		JNZ NOTADIVISOR
2013H
2014H
2015H		INR C
2016H	NOTADIVISOR	MOV A, B
2017H		DCR E
2018H		JNZ LOOP1
2019H
201AH
201BH		MOV A, C
201CH		MVI C, 00H
201DH
201EH		CPI 02H
201FH
2020H		JNZ COMPOSITE
2021H
2022H
2023H		INR C
2024H	COMPOSITE	MOV A, C
2025H		STA 202AH
2026H
2027H
2028H		HLT

将n的值存储在2029H中。如果202AH包含01H, 则n为质数, 否则为复合数。

---