本文概述
给定一个字符串s,以迭代的方式打印给定字符串的所有可能的子序列。我们已经讨论了打印字符串的所有子序列的递归方法。
例子:
Input : abc
Output : a, b, c, ab, ac, bc, abc
Input : aab
Output : a, b, aa, ab, aab推荐:请尝试以下方法{IDE}首先, 在继续解决方案之前。
方法1:
这里,我们讨论了更简单的迭代方法,它类似于幂集。我们使用二进制表示1到2^length(s) - 1的比特模式。
input =" abc"
考虑1到(2 ^ 3-1)的二进制表示形式, 即1到7。
从二进制表示形式的左(MSB)到右侧(LSB)开始, 并将与二进制表示形式的位值1相对应的输入字符串中的字符追加到Final子序列字符串sub中。
例子:
001 => abc。只有c对应于比特1。因此, 子序列= c。
101 => abc。 a和c对应于比特1。因此, 子序列= ac。
binary_representation(1)= 001 => c
binary_representation(2)= 010 => b
binary_representation(3)= 011 => bc
binary_representation(4)= 100 =>一个
binary_representation(5)= 101 =>交流
二进制表示(6)= 110 => ab
binary_representation(7)= 111 => abc
下面是上述方法的实现:
C ++
// CPP program to print all Subsequences
// of a string in iterative manner
#include <bits/stdc++.h>
using namespace std;
// function to find subsequence
string subsequence(string s, int binary, int len)
{
string sub = "" ;
for ( int j = 0; j < len; j++)
// check if jth bit in binary is 1
if (binary & (1 << j))
// if jth bit is 1, include it
// in subsequence
sub += s[j];
return sub;
}
// function to print all subsequences
void possibleSubsequences(string s){
// map to store subsequence
// lexicographically by length
map< int , set<string> > sorted_subsequence;
int len = s.size();
// Total number of non-empty subsequence
// in string is 2^len-1
int limit = pow (2, len);
// i=0, corresponds to empty subsequence
for ( int i = 1; i <= limit - 1; i++) {
// subsequence for binary pattern i
string sub = subsequence(s, i, len);
// storing sub in map
sorted_subsequence[sub.length()].insert(sub);
}
for ( auto it : sorted_subsequence) {
// it.first is length of Subsequence
// it.second is set<string>
cout << "Subsequences of length = "
<< it.first << " are:" << endl;
for ( auto ii : it.second)
// ii is iterator of type set<string>
cout << ii << " " ;
cout << endl;
}
}
// driver function
int main()
{
string s = "aabc" ;
possibleSubsequences(s);
return 0;
}Python3
# Python3 program to print all Subsequences
# of a string in iterative manner
# function to find subsequence
def subsequence(s, binary, length):
sub = ""
for j in range (length):
# check if jth bit in binary is 1
if (binary & ( 1 << j)):
# if jth bit is 1, include it
# in subsequence
sub + = s[j]
return sub
# function to print all subsequences
def possibleSubsequences(s):
# map to store subsequence
# lexicographically by length
sorted_subsequence = {}
length = len (s)
# Total number of non-empty subsequence
# in string is 2^len-1
limit = 2 * * length
# i=0, corresponds to empty subsequence
for i in range ( 1 , limit):
# subsequence for binary pattern i
sub = subsequence(s, i, length)
# storing sub in map
if len (sub) in sorted_subsequence.keys():
sorted_subsequence[ len (sub)] = \
tuple ( list (sorted_subsequence[ len (sub)]) + [sub])
else :
sorted_subsequence[ len (sub)] = [sub]
for it in sorted_subsequence:
# it.first is length of Subsequence
# it.second is set<string>
print ( "Subsequences of length =" , it, "are:" )
for ii in sorted ( set (sorted_subsequence[it])):
# ii is iterator of type set<string>
print (ii, end = ' ' )
print ()
# Driver Code
s = "aabc"
possibleSubsequences(s)
# This code is contributed by ankush_953输出如下:
Subsequences of length = 1 are:
a b c
Subsequences of length = 2 are:
aa ab ac bc
Subsequences of length = 3 are:
aab aac abc
Subsequences of length = 4 are:
aabc时间复杂度:
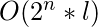
, 其中n是查找子序列的字符串的长度, l是二进制字符串的长度。
方法2:
方法是获取最右边的设置位的位置, 并在将给定字符串中的相应字符附加到子序列后重置该位, 并将重复相同的操作, 直到相应的二进制模式没有设置位为止。
如果输入为s =" abc"
考虑1到(2 ^ 3-1)的二进制表示形式, 即1到7。
001 => abc。只有c对应于比特1。因此, 子序列= c
101 => abc。 a和c对应于比特1。因此, 子序列= ac。
让我们使用5的二进制表示形式, 即101。
最右边的位在位置1, 在sub = c的开头附加字符, 重置位置1 => 100
最右边的位在位置3, 在sub = ac的开头附加字符, 重置位置3 => 000
由于现在我们没有剩余的设置位, 因此我们将停止计算子序列。
范例:
binary_representation(1)= 001 => c
binary_representation(2)= 010 => b
binary_representation(3)= 011 => bc
binary_representation(4)= 100 =>一个
binary_representation(5)= 101 =>交流
二进制表示(6)= 110 => ab
binary_representation(7)= 111 => abc
下面是上述方法的实现:
C ++
// CPP code all Subsequences of a
// string in iterative manner
#include <bits/stdc++.h>
using namespace std;
// function to find subsequence
string subsequence(string s, int binary)
{
string sub = "" ;
int pos;
// loop while binary is greater than 0
while (binary>0)
{
// get the position of rightmost set bit
pos=log2(binary&-binary)+1;
// append at beginning as we are
// going from LSB to MSB
sub=s[pos-1]+sub;
// resets bit at pos in binary
binary= (binary & ~(1 << (pos-1)));
}
reverse(sub.begin(), sub.end());
return sub;
}
// function to print all subsequences
void possibleSubsequences(string s){
// map to store subsequence
// lexicographically by length
map< int , set<string> > sorted_subsequence;
int len = s.size();
// Total number of non-empty subsequence
// in string is 2^len-1
int limit = pow (2, len);
// i=0, corresponds to empty subsequence
for ( int i = 1; i <= limit - 1; i++) {
// subsequence for binary pattern i
string sub = subsequence(s, i);
// storing sub in map
sorted_subsequence[sub.length()].insert(sub);
}
for ( auto it : sorted_subsequence) {
// it.first is length of Subsequence
// it.second is set<string>
cout << "Subsequences of length = "
<< it.first << " are:" << endl;
for ( auto ii : it.second)
// ii is iterator of type set<string>
cout << ii << " " ;
cout << endl;
}
}
// driver function
int main()
{
string s = "aabc" ;
possibleSubsequences(s);
return 0;
}Python3
# Python3 program to print all Subsequences
# of a string in an iterative manner
from math import log2, floor
# function to find subsequence
def subsequence(s, binary):
sub = ""
# loop while binary is greater than
while (binary > 0 ):
# get the position of rightmost set bit
pos = floor(log2(binary& - binary) + 1 )
# append at beginning as we are
# going from LSB to MSB
sub = s[pos - 1 ] + sub
# resets bit at pos in binary
binary = (binary & ~( 1 << (pos - 1 )))
sub = sub[:: - 1 ]
return sub
# function to print all subsequences
def possibleSubsequences(s):
# map to store subsequence
# lexicographically by length
sorted_subsequence = {}
length = len (s)
# Total number of non-empty subsequence
# in string is 2^len-1
limit = 2 * * length
# i=0, corresponds to empty subsequence
for i in range ( 1 , limit):
# subsequence for binary pattern i
sub = subsequence(s, i)
# storing sub in map
if len (sub) in sorted_subsequence.keys():
sorted_subsequence[ len (sub)] = \
tuple ( list (sorted_subsequence[ len (sub)]) + [sub])
else :
sorted_subsequence[ len (sub)] = [sub]
for it in sorted_subsequence:
# it.first is length of Subsequence
# it.second is set<string>
print ( "Subsequences of length =" , it, "are:" )
for ii in sorted ( set (sorted_subsequence[it])):
# ii is iterator of type set<string>
print (ii, end = ' ' )
print ()
# Driver Code
s = "aabc"
possibleSubsequences(s)
# This code is contributed by ankush_953输出如下:
Subsequences of length = 1 are:
a b c
Subsequences of length = 2 are:
aa ab ac bc
Subsequences of length = 3 are:
aab aac abc
Subsequences of length = 4 are:
aabc时间复杂度:
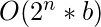
, 其中n是找到子序列的字符串的长度, b是二进制字符串中设置的位数。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)