本文概述
有向无环图(DAG)的拓扑排序是顶点的线性排序, 因此对于每个有向边u v, 顶点u在该排序中都位于v之前。如果图形不是DAG, 则无法对图形进行拓扑排序。
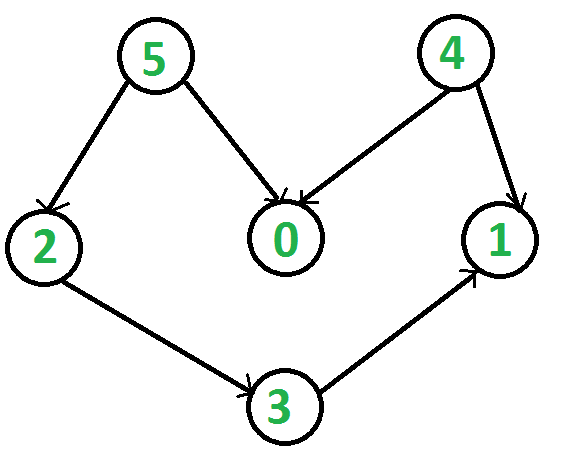
例如, 下图的拓扑排序是" 5 4 2 3 1 0"。一个图可以有多个拓扑排序。例如, 下图的另一拓扑排序是" 4 5 2 3 1 0"。拓扑排序中的第一个顶点始终是度数为0的顶点(没有输入边的顶点)。
拓扑排序与深度优先遍历(DFS):
InDFS, 我们先打印一个顶点, 然后递归调用其相邻顶点的DFS。在拓扑排序中, 我们需要在相邻顶点之前打印顶点。例如, 在给定的图形中, 顶点" 5"应在顶点" 0"之前打印, 但与DFS, 顶点" 4"也应在顶点" 0"之前打印。因此, 拓扑排序不同于DFS。例如, 所示图形的DFS为" 5 2 3 1 0 4", 但这不是拓扑排序。
推荐:请在"
实践
首先, 在继续解决方案之前。
查找拓扑排序的算法:
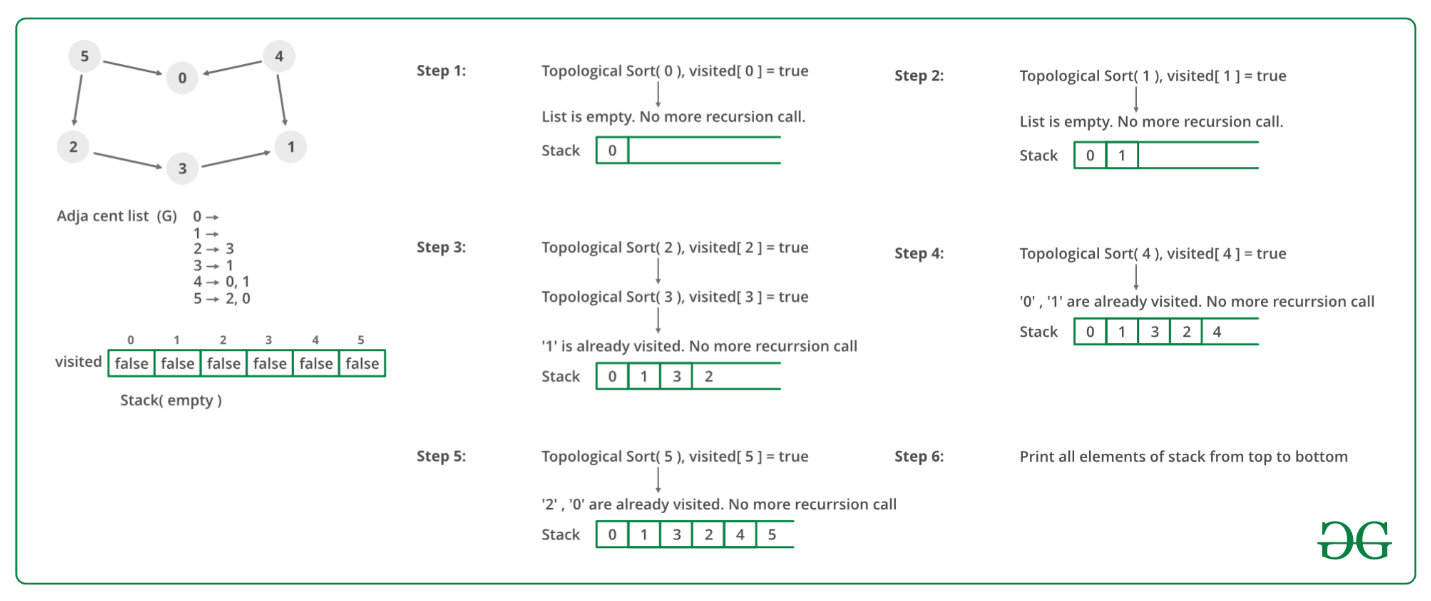
我们建议先看看执行情况DFS。我们可以修改DFS查找图的拓扑排序。在DFS, 我们从一个顶点开始, 首先打印它, 然后递归调用其相邻顶点的DFS。在拓扑排序中, 我们使用临时堆栈。我们不会立即打印顶点, 而是首先对其所有相邻顶点递归调用拓扑排序, 然后将其推入堆栈。最后, 打印堆栈中的内容。请注意, 仅当顶点的所有相邻顶点(及其相邻顶点等)都已在堆栈中时, 才将其推入堆栈。
下图说明了上述方法:
以下是拓扑排序的实现。请查看深度代码断开图的首次遍历并注意此处给出的第二个代码与下面的代码之间的区别。
C ++
// A C++ program to print topological
// sorting of a DAG
#include <iostream>
#include <list>
#include <stack>
using namespace std;
// Class to represent a graph
class Graph {
// No. of vertices'
int V;
// Pointer to an array containing adjacency listsList
list< int >* adj;
// A function used by topologicalSort
void topologicalSortUtil( int v, bool visited[], stack< int >& Stack);
public :
// Constructor
Graph( int V);
// function to add an edge to graph
void addEdge( int v, int w);
// prints a Topological Sort of
// the complete graph
void topologicalSort();
};
Graph::Graph( int V)
{
this ->V = V;
adj = new list< int >[V];
}
void Graph::addEdge( int v, int w)
{
// Add w to v’s list.
adj[v].push_back(w);
}
// A recursive function used by topologicalSort
void Graph::topologicalSortUtil( int v, bool visited[], stack< int >& Stack)
{
// Mark the current node as visited.
visited[v] = true ;
// Recur for all the vertices
// adjacent to this vertex
list< int >::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
if (!visited[*i])
topologicalSortUtil(*i, visited, Stack);
// Push current vertex to stack
// which stores result
Stack.push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void Graph::topologicalSort()
{
stack< int > Stack;
// Mark all the vertices as not visited
bool * visited = new bool [V];
for ( int i = 0; i < V; i++)
visited[i] = false ;
// Call the recursive helper function
// to store Topological
// Sort starting from all
// vertices one by one
for ( int i = 0; i < V; i++)
if (visited[i] == false )
topologicalSortUtil(i, visited, Stack);
// Print contents of stack
while (Stack.empty() == false ) {
cout << Stack.top() << " " ;
Stack.pop();
}
}
// Driver Code
int main()
{
// Create a graph given in the above diagram
Graph g(6);
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
cout << "Following is a Topological Sort of the given "
"graph \n" ;
// Function Call
g.topologicalSort();
return 0;
}Java
// A Java program to print topological
// sorting of a DAG
import java.io.*;
import java.util.*;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency List as ArrayList of ArrayList's
private ArrayList<ArrayList<Integer> > adj;
// Constructor
Graph( int v)
{
V = v;
adj = new ArrayList<ArrayList<Integer> >(v);
for ( int i = 0 ; i < v; ++i)
adj.add( new ArrayList<Integer>());
}
// Function to add an edge into the graph
void addEdge( int v, int w) { adj.get(v).add(w); }
// A recursive function used by topologicalSort
void topologicalSortUtil( int v, boolean visited[], Stack<Integer> stack)
{
// Mark the current node as visited.
visited[v] = true ;
Integer i;
// Recur for all the vertices adjacent
// to thisvertex
Iterator<Integer> it = adj.get(v).iterator();
while (it.hasNext()) {
i = it.next();
if (!visited[i])
topologicalSortUtil(i, visited, stack);
}
// Push current vertex to stack
// which stores result
stack.push( new Integer(v));
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void topologicalSort()
{
Stack<Integer> stack = new Stack<Integer>();
// Mark all the vertices as not visited
boolean visited[] = new boolean [V];
for ( int i = 0 ; i < V; i++)
visited[i] = false ;
// Call the recursive helper
// function to store
// Topological Sort starting
// from all vertices one by one
for ( int i = 0 ; i < V; i++)
if (visited[i] == false )
topologicalSortUtil(i, visited, stack);
// Print contents of stack
while (stack.empty() == false )
System.out.print(stack.pop() + " " );
}
// Driver code
public static void main(String args[])
{
// Create a graph given in the above diagram
Graph g = new Graph( 6 );
g.addEdge( 5 , 2 );
g.addEdge( 5 , 0 );
g.addEdge( 4 , 0 );
g.addEdge( 4 , 1 );
g.addEdge( 2 , 3 );
g.addEdge( 3 , 1 );
System.out.println( "Following is a Topological "
+ "sort of the given graph" );
// Function Call
g.topologicalSort();
}
}
// This code is contributed by Aakash Hasijapython
# Python program to print topological sorting of a DAG
from collections import defaultdict
# Class to represent a graph
class Graph:
def __init__( self , vertices):
self .graph = defaultdict( list ) # dictionary containing adjacency List
self .V = vertices # No. of vertices
# function to add an edge to graph
def addEdge( self , u, v):
self .graph[u].append(v)
# A recursive function used by topologicalSort
def topologicalSortUtil( self , v, visited, stack):
# Mark the current node as visited.
visited[v] = True
# Recur for all the vertices adjacent to this vertex
for i in self .graph[v]:
if visited[i] = = False :
self .topologicalSortUtil(i, visited, stack)
# Push current vertex to stack which stores result
stack.append(v)
# The function to do Topological Sort. It uses recursive
# topologicalSortUtil()
def topologicalSort( self ):
# Mark all the vertices as not visited
visited = [ False ] * self .V
stack = []
# Call the recursive helper function to store Topological
# Sort starting from all vertices one by one
for i in range ( self .V):
if visited[i] = = False :
self .topologicalSortUtil(i, visited, stack)
# Print contents of the stack
print stack[:: - 1 ] # return list in reverse order
# Driver Code
g = Graph( 6 )
g.addEdge( 5 , 2 )
g.addEdge( 5 , 0 )
g.addEdge( 4 , 0 )
g.addEdge( 4 , 1 )
g.addEdge( 2 , 3 )
g.addEdge( 3 , 1 )
print "Following is a Topological Sort of the given graph"
# Function Call
g.topologicalSort()
# This code is contributed by Neelam YadavC#
// A C# program to print topological
// sorting of a DAG
using System;
using System.Collections.Generic;
// This class represents a directed graph
// using adjacency list representation
class Graph {
// No. of vertices
private int V;
// Adjacency List as ArrayList
// of ArrayList's
private List<List< int > > adj;
// Constructor
Graph( int v)
{
V = v;
adj = new List<List< int > >(v);
for ( int i = 0; i < v; i++)
adj.Add( new List< int >());
}
// Function to add an edge into the graph
public void AddEdge( int v, int w) { adj[v].Add(w); }
// A recursive function used by topologicalSort
void TopologicalSortUtil( int v, bool [] visited, Stack< int > stack)
{
// Mark the current node as visited.
visited[v] = true ;
// Recur for all the vertices
// adjacent to this vertex
foreach ( var vertex in adj[v])
{
if (!visited[vertex])
TopologicalSortUtil(vertex, visited, stack);
}
// Push current vertex to
// stack which stores result
stack.Push(v);
}
// The function to do Topological Sort.
// It uses recursive topologicalSortUtil()
void TopologicalSort()
{
Stack< int > stack = new Stack< int >();
// Mark all the vertices as not visited
var visited = new bool [V];
// Call the recursive helper function
// to store Topological Sort starting
// from all vertices one by one
for ( int i = 0; i < V; i++) {
if (visited[i] == false )
TopologicalSortUtil(i, visited, stack);
}
// Print contents of stack
foreach ( var vertex in stack)
{
Console.Write(vertex + " " );
}
}
// Driver code
public static void Main( string [] args)
{
// Create a graph given
// in the above diagram
Graph g = new Graph(6);
g.AddEdge(5, 2);
g.AddEdge(5, 0);
g.AddEdge(4, 0);
g.AddEdge(4, 1);
g.AddEdge(2, 3);
g.AddEdge(3, 1);
Console.WriteLine( "Following is a Topological "
+ "sort of the given graph" );
// Function Call
g.TopologicalSort();
}
}
// This code is contributed by Abhinav Galodha输出如下
Following is a Topological Sort of the given graph
5 4 2 3 1 0复杂度分析:
- 时间复杂度:O(V + E)。
上面的算法只是带有额外堆栈的DFS。因此, 时间复杂度与DFS相同。 - 辅助空间:O(V)。
堆栈需要额外的空间。
注意:在这里, 我们也可以使用向量代替堆栈。如果使用矢量, 则以相反顺序打印元素以进行拓扑排序。
应用范围:
拓扑排序主要用于根据作业之间的给定依赖性来调度作业。在计算机科学中, 这种类型的应用出现在指令调度, 重新计算电子表格中的公式值时公式单元格评估的顺序, 逻辑综合, 确定要在make文件中执行的编译任务的顺序, 数据序列化以及解析链接器中的符号依存关系[
2
]。
相关文章:
卡恩的拓扑排序算法
:另一种O(V + E)算法。
有向无环图的所有拓扑排序
参考文献:
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/GraphAlgor/topoSort.htm
http://en.wikipedia.org/wiki/Topological_sorting
如果发现任何不正确的地方, 或者你想分享有关上述主题的更多信息, 请发表评论

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)