算法设计：非重叠的连续子数组的K个最大和

2021年3月16日12:07:02 发表评论 820 次浏览

本文概述

给定一个整数数组和一个整数值k, 找出k个最大和为k的非重叠子数组。

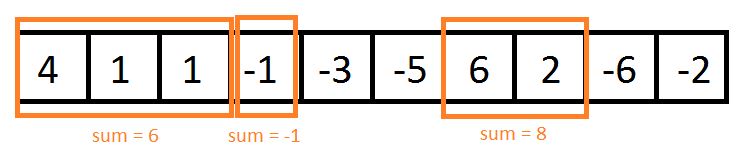
非重叠的连续子数组的K个最大和1

例子：

Input : arr1[] = {4, 1, 1, -1, -3, -5, 6, 2, -6, -2}, k = 3.
Output : Maximum non-overlapping sub-array sum1: 8, starting index: 6, ending index: 7.
         
         Maximum non-overlapping sub-array sum2: 6, starting index: 0, ending index: 2.
         
         Maximum non-overlapping sub-array sum3: -1, starting index: 3, ending index: 3.

Input : arr2 = {5, 1, 2, -6, 2, -1, 3, 1}, k = 2.
Output : Maximum non-overlapping sub-array sum1: 8, starting index: 0, ending index: 2.

         Maximum non-overlapping sub-array sum2: 5, starting index: 4, ending index: 7.

推荐：请尝试以下方法{IDE}首先, 在继续解决方案之前。

先决条件： Kadane的算法

Kadane的算法仅找出最大子阵列和, 但是使用相同的算法, 我们可以找出k个最大非重叠子阵列和。方法是：

  • 使用Kadane的算法找出阵列中的最大子阵列。还找出其开始和结束索引。打印此子数组的总和。
  • 用-infinity填充此子数组的每个单元格。
  • 重复过程1和2 k次。

C ++

// C++ program to find out k maximum 
// non-overlapping sub-array sums.
#include <bits/stdc++.h>
using namespace std;
  
// Function to compute k maximum
// sub-array sums.
void kmax( int arr[], int k, int n) {
  
     // In each iteration it will give
     // the ith maximum subarray sum.
     for ( int c = 0; c < k; c++){
  
         // Kadane's algorithm.
         int max_so_far = numeric_limits< int >::min();
         int max_here = 0;
  
         // compute starting and ending
         // index of each of the sub-array.
         int start = 0, end = 0, s = 0;
         for ( int i = 0; i < n; i++)
         {
             max_here += arr[i];
             if (max_so_far < max_here)
             {
                 max_so_far = max_here;
                 start = s;
                 end = i;
             }
             if (max_here < 0)
             {
                 max_here = 0;
                 s = i + 1;
             }
         }
  
         // Print out the result.
         cout << "Maximum non-overlapping sub-array sum"
              << (c + 1) << ": " << max_so_far 
              << ", starting index: " << start 
              << ", ending index: " << end << "." << endl;
  
         // Replace all elements of the maximum subarray 
         // by -infinity. Hence these places cannot form 
         // maximum sum subarray again.
         for ( int l = start; l <= end; l++)
             arr[l] = numeric_limits< int >::min();
     }
     cout << endl;
}
  
// Driver Program
int main()
{
     // Test case 1
     int arr1[] = {4, 1, 1, -1, -3, -5, 6, 2, -6, -2};
     int k1 = 3;
     int n1 = sizeof (arr1) / sizeof (arr1[0]);
      
     // Function calling
     kmax(arr1, k1, n1);
  
     // Test case 2
     int arr2[] = {5, 1, 2, -6, 2, -1, 3, 1};
     int k2 = 2;
     int n2 = sizeof (arr2)/ sizeof (arr2[0]);
      
     // Function calling
     kmax(arr2, k2, n2);
      
     return 0;
}

Java

// Java program to find out k maximum 
// non-overlapping sub-array sums.
  
class GFG {
  
     // Method to compute k maximum 
     // sub-array sums.
     static void kmax( int arr[], int k, int n) {
      
         // In each iteration it will give
         // the ith maximum subarray sum.
         for ( int c = 0 ; c < k; c++)
         { 
             // Kadane's algorithm.
             int max_so_far = Integer.MIN_VALUE;
             int max_here = 0 ;
      
             // compute starting and ending
             // index of each of the sub-array.
             int start = 0 , end = 0 , s = 0 ;
             for ( int i = 0 ; i < n; i++)
             {
                 max_here += arr[i];
                 if (max_so_far < max_here)
                 {
                     max_so_far = max_here;
                     start = s;
                     end = i;
                 }
                 if (max_here < 0 )
                     {
                     max_here = 0 ;
                     s = i + 1 ;
                 }
             }
      
             // Print out the result.
             System.out.println( "Maximum non-overlapping sub-arraysum" +
                                 (c + 1 ) + ": " +  max_so_far + 
                                 ", starting index: " + start +
                                 ", ending index: " + end + "." );
      
             // Replace all elements of the maximum subarray 
             // by -infinity. Hence these places cannot form 
             // maximum sum subarray again.
             for ( int l = start; l <= end; l++)
                 arr[l] = Integer.MIN_VALUE;
         }
         System.out.println();
     }
      
     // Driver Program
     public static void main(String[] args)
     {
         // Test case 1
         int arr1[] = { 4 , 1 , 1 , - 1 , - 3 , - 5 , 6 , 2 , - 6 , - 2 };
         int k1 = 3 ;
         int n1 = arr1.length;
          
         // Function calling
         kmax(arr1, k1, n1);
      
         // Test case 2
         int arr2[] = { 5 , 1 , 2 , - 6 , 2 , - 1 , 3 , 1 };
         int k2 = 2 ;
         int n2 = arr2.length;
          
         // Function calling
         kmax(arr2, k2, n2);
     }
}
  
// This code is contributed by Nirmal Patel

Python3

# Python program to find out k maximum 
# non-overlapping subarray sums.
  
# Function to compute k 
# maximum sub-array sums.
def kmax(arr, k, n):
  
     # In each iteration it will give
     # the ith maximum subarray sum.
     for c in range (k):
  
         # Kadane's algorithm
         max_so_far = - float ( "inf" )
         max_here = 0
  
         # compute starting and ending
         # index of each of the subarray
         start = 0
         end = 0
         s = 0
         for i in range (n):
              
             max_here + = arr[i]
             if (max_so_far < max_here):
                  
                 max_so_far = max_here
                 start = s
                 end = i
             if (max_here < 0 ):
                  
                 max_here = 0
                 s = i + 1
  
         # Print out the result
         print ( "Maximum non-overlapping sub-array sum" , c + 1 , ": " , max_so_far, ", starting index: " , start, ", ending index: " , end, "." , sep = "")
  
         # Replace all elements of the maximum subarray
         # by -infinity. Hence these places cannot form 
         # maximum sum subarray again.
         for l in range (start, end + 1 ):
             arr[l] = - float ( "inf" )
     print ()
  
# Driver Program
# Test case 1
arr1 = [ 4 , 1 , 1 , - 1 , - 3 , - 5 , 6 , 2 , - 6 , - 2 ]
k1 = 3
n1 = len (arr1)
  
# Function calling
kmax(arr1, k1, n1)
  
# Test case 2
arr2 = [ 5 , 1 , 2 , - 6 , 2 , - 1 , 3 , 1 ]
k2 = 2
n2 = len (arr2)
  
# Function calling
kmax(arr2, k2, n2)

C#

// C# program to find out k maximum 
// non-overlapping sub-array sums.
using System;
  
class GFG {
  
     // Method to compute k 
     // maximum sub-array sums.
     static void kmax( int []arr, int k, int n) {
      
         // In each iteration it will give
         // the ith maximum subarray sum.
         for ( int c = 0; c < k; c++)
         { 
             // Kadane's algorithm.
             int max_so_far = int .MinValue;
             int max_here = 0;
      
             // compute starting and ending
             // index of each of the sub-array.
             int start = 0, end = 0, s = 0;
             for ( int i = 0; i < n; i++)
             {
                 max_here += arr[i];
                 if (max_so_far < max_here)
                 {
                     max_so_far = max_here;
                     start = s;
                     end = i;
                 }
                 if (max_here < 0)
                 {
                     max_here = 0;
                     s = i + 1;
                 }
             }
      
             // Print out the result.
             Console.WriteLine( "Maximum non-overlapping sub-arraysum" +
                               (c + 1) + ": " + max_so_far + 
                               ", starting index: " + start + 
                               ", ending index: " + end + "." );
      
             // Replace all elements of the maximum subarray 
             // by -infinity. Hence these places cannot form 
             // maximum sum subarray again.
             for ( int l = start; l <= end; l++)
                 arr[l] = int .MinValue;
         }
     Console.WriteLine();
     }
      
     // Driver Program
     public static void Main(String[] args)
     {
         // Test case 1
         int []arr1 = {4, 1, 1, -1, -3, -5, 6, 2, -6, -2};
         int k1 = 3;
         int n1 = arr1.Length;
          
         // Function calling
         kmax(arr1, k1, n1);
      
         // Test case 2
         int []arr2 = {5, 1, 2, -6, 2, -1, 3, 1};
         int k2 = 2;
         int n2 = arr2.Length;
          
         // Function calling
         kmax(arr2, k2, n2);
     }
}
  
// This code is contributed by parashar...

的PHP

<?php
// PHP program to find out k maximum 
// non-overlapping sub-array sums.
  
     // Method to compute k 
     // maximum sub-array sums.
     function kmax( $arr , $k , $n ) {
      
         // In each iteration it will give
         // the ith maximum subarray sum.
         for ( $c = 0; $c < $k ; $c ++)
         { 
             // Kadane's algorithm.
             $max_so_far = PHP_INT_MIN;
             $max_here = 0;
      
             // compute starting and ending
             // index of each of the sub-array.
             $start = 0; $end = 0; $s = 0;
             for ( $i = 0; $i < $n ; $i ++)
             {
                 $max_here += $arr [ $i ];
                 if ( $max_so_far < $max_here )
                 {
                     $max_so_far = $max_here ;
                     $start = $s ;
                     $end = $i ;
                 }
                 if ( $max_here < 0)
                 {
                     $max_here = 0;
                     $s = $i + 1;
                 }
             }
      
             // Print out the result.
             echo "Maximum non-overlapping sub-arraysum" ;
             echo ( $c + 1) , ": " , $max_so_far ; 
             echo ", starting index: " , $start ;
             echo ", ending index: " , $end , "." ;
             echo "\n" ;
      
             // Replace all elements of the maximum subarray 
             // by -infinity. Hence these places cannot form 
             // maximum sum subarray again.
             for ( $l = $start ; $l <= $end ; $l ++)
                 $arr [ $l ] = PHP_INT_MIN;
         }
         echo "\n" ;
     }
      
     // Driver Program
         // Test case 1
         $arr1 = array (4, 1, 1, -1, -3, -5, 6, 2, -6, -2);
         $k1 = 3;
         $n1 = count ( $arr1 );
          
         // Function calling
         kmax( $arr1 , $k1 , $n1 );
      
         // Test case 2
         $arr2 = array (5, 1, 2, -6, 2, -1, 3, 1);
         $k2 = 2;
         $n2 = count ( $arr2 );
          
         // Function calling
         kmax( $arr2 , $k2 , $n2 );
  
// This code is contributed by anuj_67.
?>

输出如下：

Maximum non-overlapping sub-array sum1: 8, starting index: 6, ending index: 7.
Maximum non-overlapping sub-array sum2: 6, starting index: 0, ending index: 2.
Maximum non-overlapping sub-array sum3: -1, starting index: 3, ending index: 3.

Maximum non-overlapping sub-array sum1: 8, starting index: 0, ending index: 2.
Maximum non-overlapping sub-array sum2: 5, starting index: 4, ending index: 7.

时间复杂度：

外循环运行k次, kadane的算法在每次迭代中以线性时间O(n)运行。因此, 总的时间复杂度为O(k * n)。

木子山

发表评论

:?: :razz: :sad: :evil: :!: :smile: :oops: :grin: :eek: :shock: :???: :cool: :lol: :mad: :twisted: :roll: :wink: :idea: :arrow: :neutral: :cry: :mrgreen: