本文概述
N Queen是在N×N棋盘上放置N个国际象棋皇后的问题, 这样就不会有两个女王互相攻击。例如, 以下是4 Queen问题的解决方案。
N Queen是在N×N棋盘上放置N个国际象棋皇后的问题, 这样就不会有两个女王互相攻击。例如, 以下是4 Queen问题的两个解决方案。
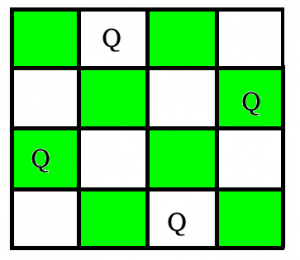
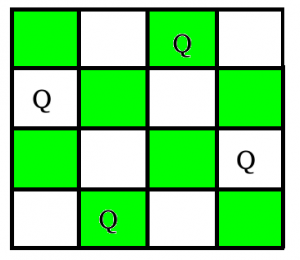
In
以前
帖子中, 我们讨论了一种仅打印一种可能的解决方案的方法, 因此, 现在本文中的任务是打印N-Queen问题中的所有解决方案。这里讨论的解决方案是相同方法的扩展。
推荐:请尝试以下方法
{IDE}
首先, 在继续解决方案之前。
这个想法是将皇后区从最左边的列开始一个一列地放置在不同的列中。当我们在一个列中放置一个皇后时, 我们检查是否与已经放置的皇后发生冲突。在当前列中, 如果找到没有冲突的行, 则将该行和列标记为解决方案的一部分。如果由于冲突而找不到这样的行, 那么我们将回溯并返回false。
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column. Do following
for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing queen in [row, column] leads to a
solution then return true.
c) If placing queen doesn't lead to a solution
then unmark this [row, column] (Backtrack)
and go to step (a) to try other rows.
3) If all rows have been tried and nothing worked, return false to trigger backtracking.在代码中突出显示的上述算法只有一点修改。
C ++
/* C/C++ program to solve N Queen Problem using
backtracking */
#include<bits/stdc++.h>
#define N 4
/* A utility function to print solution */
void printSolution( int board[N][N])
{
static int k = 1;
printf ( "%d-\n" , k++);
for ( int i = 0; i < N; i++)
{
for ( int j = 0; j < N; j++)
printf ( " %d " , board[i][j]);
printf ( "\n" );
}
printf ( "\n" );
}
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens */
bool isSafe( int board[N][N], int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0; i < col; i++)
if (board[row][i])
return false ;
/* Check upper diagonal on left side */
for (i=row, j=col; i>=0 && j>=0; i--, j--)
if (board[i][j])
return false ;
/* Check lower diagonal on left side */
for (i=row, j=col; j>=0 && i<N; i++, j--)
if (board[i][j])
return false ;
return true ;
}
/* A recursive utility function to solve N
Queen problem */
bool solveNQUtil( int board[N][N], int col)
{
/* base case: If all queens are placed
then return true */
if (col == N)
{
printSolution(board);
return true ;
}
/* Consider this column and try placing
this queen in all rows one by one */
bool res = false ;
for ( int i = 0; i < N; i++)
{
/* Check if queen can be placed on
board[i][col] */
if ( isSafe(board, i, col) )
{
/* Place this queen in board[i][col] */
board[i][col] = 1;
// Make result true if any placement
// is possible
res = solveNQUtil(board, col + 1) || res;
/* If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] */
board[i][col] = 0; // BACKTRACK
}
}
/* If queen can not be place in any row in
this column col then return false */
return res;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
void solveNQ()
{
int board[N][N];
memset (board, 0, sizeof (board));
if (solveNQUtil(board, 0) == false )
{
printf ( "Solution does not exist" );
return ;
}
return ;
}
// driver program to test above function
int main()
{
solveNQ();
return 0;
}Java
/* Java program to solve N Queen
Problem using backtracking */
class GfG
{
static int N = 4 ;
static int k = 1 ;
/* A utility function to print solution */
static void printSolution( int board[][])
{
System.out.printf( "%d-\n" , k++);
for ( int i = 0 ; i < N; i++)
{
for ( int j = 0 ; j < N; j++)
System.out.printf( " %d " , board[i][j]);
System.out.printf( "\n" );
}
System.out.printf( "\n" );
}
/* A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens */
static boolean isSafe( int board[][], int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0 ; i < col; i++)
if (board[row][i] == 1 )
return false ;
/* Check upper diagonal on left side */
for (i = row, j = col; i >= 0 && j >= 0 ; i--, j--)
if (board[i][j] == 1 )
return false ;
/* Check lower diagonal on left side */
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1 )
return false ;
return true ;
}
/* A recursive utility function
to solve N Queen problem */
static boolean solveNQUtil( int board[][], int col)
{
/* base case: If all queens are placed
then return true */
if (col == N)
{
printSolution(board);
return true ;
}
/* Consider this column and try placing
this queen in all rows one by one */
boolean res = false ;
for ( int i = 0 ; i < N; i++)
{
/* Check if queen can be placed on
board[i][col] */
if ( isSafe(board, i, col) )
{
/* Place this queen in board[i][col] */
board[i][col] = 1 ;
// Make result true if any placement
// is possible
res = solveNQUtil(board, col + 1 ) || res;
/* If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] */
board[i][col] = 0 ; // BACKTRACK
}
}
/* If queen can not be place in any row in
this column col then return false */
return res;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
static void solveNQ()
{
int board[][] = new int [N][N];
if (solveNQUtil(board, 0 ) == false )
{
System.out.printf( "Solution does not exist" );
return ;
}
return ;
}
// Driver code
public static void main(String[] args)
{
solveNQ();
}
}
// This code has been contributed
// by 29AjayKumarPython3
''' Python3 program to solve N Queen Problem using
backtracking '''
k = 1
# A utility function to print solution
def printSolution(board):
global k
print (k, "-\n" )
k = k + 1
for i in range ( 4 ):
for j in range ( 4 ):
print (board[i][j], end = " " )
print ( "\n" )
print ( "\n" )
''' A utility function to check if a queen can
be placed on board[row][col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens '''
def isSafe(board, row, col) :
# Check this row on left side
for i in range (col):
if (board[row][i]):
return False
# Check upper diagonal on left side
i = row
j = col
while i > = 0 and j > = 0 :
if (board[i][j]):
return False ;
i - = 1
j - = 1
# Check lower diagonal on left side
i = row
j = col
while j > = 0 and i < 4 :
if (board[i][j]):
return False
i = i + 1
j = j - 1
return True
''' A recursive utility function to solve N
Queen problem '''
def solveNQUtil(board, col) :
''' base case: If all queens are placed
then return true '''
if (col = = 4 ):
printSolution(board)
return True
''' Consider this column and try placing
this queen in all rows one by one '''
res = False
for i in range ( 4 ):
''' Check if queen can be placed on
board[i][col] '''
if (isSafe(board, i, col)):
# Place this queen in board[i][col]
board[i][col] = 1 ;
# Make result true if any placement
# is possible
res = solveNQUtil(board, col + 1 ) or res;
''' If placing queen in board[i][col]
doesn't lead to a solution, then
remove queen from board[i][col] '''
board[i][col] = 0 # BACKTRACK
''' If queen can not be place in any row in
this column col then return false '''
return res
''' This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.'''
def solveNQ() :
board = [[ 0 for j in range ( 10 )]
for i in range ( 10 )]
if (solveNQUtil(board, 0 ) = = False ):
print ( "Solution does not exist" )
return
return
# Driver Code
solveNQ()
# This code is contributed by YatinGuptaC#
/* C# program to solve N Queen
Problem using backtracking */
using System;
class GfG
{
static int N = 4;
static int k = 1;
/* A utility function to print solution */
static void printSolution( int [, ]board)
{
Console.Write( "{0}-\n" , k++);
for ( int i = 0; i < N; i++)
{
for ( int j = 0; j < N; j++)
Console.Write( " {0} " , board[i, j]);
Console.Write( "\n" );
}
Console.Write( "\n" );
}
/* A utility function to check if a queen can
be placed on board[row, col]. Note that this
function is called when "col" queens are
already placed in columns from 0 to col -1.
So we need to check only left side for
attacking queens */
static bool isSafe( int [, ]board, int row, int col)
{
int i, j;
/* Check this row on left side */
for (i = 0; i < col; i++)
if (board[row, i] == 1)
return false ;
/* Check upper diagonal on left side */
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i, j] == 1)
return false ;
/* Check lower diagonal on left side */
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i, j] == 1)
return false ;
return true ;
}
/* A recursive utility function
to solve N Queen problem */
static bool solveNQUtil( int [, ]board, int col)
{
/* base case: If all queens are placed
then return true */
if (col == N)
{
printSolution(board);
return true ;
}
/* Consider this column and try placing
this queen in all rows one by one */
bool res = false ;
for ( int i = 0; i < N; i++)
{
/* Check if queen can be placed on
board[i, col] */
if ( isSafe(board, i, col) )
{
/* Place this queen in board[i, col] */
board[i, col] = 1;
// Make result true if any placement
// is possible
res = solveNQUtil(board, col + 1) || res;
/* If placing queen in board[i, col]
doesn't lead to a solution, then
remove queen from board[i, col] */
board[i, col] = 0; // BACKTRACK
}
}
/* If queen can not be place in any row in
this column col then return false */
return res;
}
/* This function solves the N Queen problem using
Backtracking. It mainly uses solveNQUtil() to
solve the problem. It returns false if queens
cannot be placed, otherwise return true and
prints placement of queens in the form of 1s.
Please note that there may be more than one
solutions, this function prints one of the
feasible solutions.*/
static void solveNQ()
{
int [, ]board = new int [N, N];
if (solveNQUtil(board, 0) == false )
{
Console.Write( "Solution does not exist" );
return ;
}
return ;
}
// Driver code
public static void Main()
{
solveNQ();
}
}
/* This code contributed by PrinciRaj1992 */输出如下
1-
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
2-
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0输出如下:
1-
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
2-
0 1 0 0
0 0 0 1
1 0 0 0
0 0 1 0C ++
// CPP program for above approach
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
// Program to print board
void printBoard(vector< vector< char > >& board)
{
for ( auto row : board)
{
cout<< "|" ;
for ( auto ch : row)
{
cout<<ch<< "|" ;
}
cout<<endl;
}
}
// Program to solve N Quuens problem
void solveBoard(vector<vector< char > >& board, int row, int rowmask, int ldmask, int rdmask, int & ways)
{
int n = board.size();
// All_rows_filled is a bit mask having all N bits set
int all_rows_filled = (1 << n) - 1;
// If rowmask will have all bits set, means queen has been
// placed successfully in all rows and board is diplayed
if (rowmask == all_rows_filled)
{
ways++;
cout<< "=====================\n" ;
cout<< "Queen placement - " <<ways<<endl;
cout<< "=====================\n" ;
printBoard(board);
return ;
}
// We extract a bit mask(safe) by rowmask, // ldmask and rdmask. all set bits of 'safe'
// indicates the safe column index for queen
// placement of this iteration for row index(row).
int safe = all_rows_filled & (~(rowmask |
ldmask | rdmask));
while (safe)
{
// Extracts the right-most set bit
// (safe column index) where queen
// can be placed for this row
int p = safe & (-safe);
int col = ( int )log2(p);
board[row][col] = 'Q' ;
// This is very important:
// we need to update rowmask, ldmask and rdmask
// for next row as safe index for queen placement
// will be decided by these three bit masks.
// We have all three rowmask, ldmask and
// rdmask as 0 in beginning. Suppose, we are placing
// queen at 1st column index at 0th row. rowmask, ldmask
// and rdmask will change for next row as below:
// rowmask's 1st bit will be set by OR operation
// rowmask = 00000000000000000000000000000010
// ldmask will change by setting 1st
// bit by OR operation and left shifting
// by 1 as it has to block the next column
// of next row because that will fall on left diagonal.
// ldmask = 00000000000000000000000000000100
// rdmask will change by setting 1st bit
// by OR operation and right shifting by 1
// as it has to block the previous column
// of next row because that will fall on right diagonal.
// rdmask = 00000000000000000000000000000001
// these bit masks will keep updated in each
// iteration for next row
solveBoard(board, row+1, rowmask|p, (ldmask|p) << 1, (rdmask|p) >> 1, ways);
// Reset right-most set bit to 0 so, // next iteration will continue by placing the queen
// at another safe column index of this row
safe = safe & (safe-1);
// Backtracking, replace 'Q' by ' '
board[row][col] = ' ' ;
}
return ;
}
// Driver Code
int main()
{
// Board size
int n = 4;
int ways = 0;
vector< vector< char > > board;
for ( int i = 0; i < n; i++)
{
vector< char > tmp;
for ( int j = 0; j < n; j++)
{
tmp.push_back( ' ' );
}
board.push_back(tmp);
}
int rowmask = 0, ldmask = 0, rdmask = 0;
int row = 0;
// Function Call
solveBoard(board, row, rowmask, ldmask, rdmask, ways);
cout<<endl<< "Number of ways to place " <<n<< " queens : "
<<ways<<endl;
return 0;
}
// This code is contributed by Nikhil VinayJava
// Java Program for aove approach
public class NQueenSolution
{
static private int ways = 0 ;
// Program to solve N-Queens Problem
public void solveBoard( char [][] board, int row, int rowmask, int ldmask, int rdmask)
{
int n = board.length;
// All_rows_filled is a bit mask
// having all N bits set
int all_rows_filled = ( 1 << n) - 1 ;
// If rowmask will have all bits set, // means queen has been placed successfully
// in all rows and board is diplayed
if (rowmask == all_rows_filled)
{
ways++;
System.out.println( "=====================" );
System.out.println( "Queen placement - " + ways);
System.out.println( "=====================" );
printBoard(board);
}
// We extract a bit mask(safe) by rowmask, // ldmask and rdmask. all set bits of 'safe'
// indicates the safe column index for queen
// placement of this iteration for row index(row).
int safe = all_rows_filled & (~(rowmask |
ldmask | rdmask));
while (safe > 0 )
{
// Extracts the right-most set bit
// (safe column index) where queen
// can be placed for this row
int p = safe & (-safe);
int col = ( int )(Math.log(p) / Math.log( 2 ));
board[row][col] = 'Q' ;
// This is very important:
// we need to update rowmask, ldmask and rdmask
// for next row as safe index for queen placement
// will be decided by these three bit masks.
// We have all three rowmask, ldmask and
// rdmask as 0 in beginning. Suppose, we are placing
// queen at 1st column index at 0th row. rowmask, ldmask
// and rdmask will change for next row as below:
// rowmask's 1st bit will be set by OR operation
// rowmask = 00000000000000000000000000000010
// ldmask will change by setting 1st
// bit by OR operation and left shifting
// by 1 as it has to block the next column
// of next row because that will fall on left diagonal.
// ldmask = 00000000000000000000000000000100
// rdmask will change by setting 1st bit
// by OR operation and right shifting by 1
// as it has to block the previous column
// of next row because that will fall on right diagonal.
// rdmask = 00000000000000000000000000000001
// these bit masks will keep updated in each
// iteration for next row
solveBoard(board, row+ 1 , rowmask|p, (ldmask|p) << 1 , (rdmask|p) >> 1 );
// Reset right-most set bit to 0 so, // next iteration will continue by placing the queen
// at another safe column index of this row
safe = safe & (safe- 1 );
// Backtracking, replace 'Q' by ' '
board[row][col] = ' ' ;
}
}
// Program to print board
public void printBoard( char [][] board)
{
for ( int i = 0 ; i < board.length; i++)
{
System.out.print( "|" );
for ( int j = 0 ; j < board[i].length; j++)
{
System.out.print(board[i][j] + "|" );
}
System.out.println();
}
}
// Driver Code
public static void main(String args[])
{
// Board size
int n = 4 ;
char board[][] = new char [n][n];
for ( int i = 0 ; i < n; i++)
{
for ( int j = 0 ; j < n; j++)
{
board[i][j] = ' ' ;
}
}
int rowmask = 0 , ldmask = 0 , rdmask = 0 ;
int row = 0 ;
NQueenSolution solution = new
NQueenSolution();
// Function Call
solution.solveBoard(board, row, rowmask, ldmask, rdmask);
System.out.println();
System.out.println( "Number of ways to place " +
n + " queens : " + ways);
}
}
// This code is contributed by Nikhil VinayPython3
# Python program for above approach
import math
ways = 0
# Program to solve N-Queens Problem
def solveBoard(board, row, rowmask, ldmask, rdmask):
n = len (board)
# All_rows_filled is a bit mask
# having all N bits set
all_rows_filled = ( 1 << n) - 1
# If rowmask will have all bits set, means
# queen has been placed successfully
# in all rows and board is diplayed
if (rowmask = = all_rows_filled):
global ways
ways = ways + 1
print ( "=====================" )
print ( "Queen placement - " + ( str )(ways))
print ( "=====================" )
printBoard(board)
# We extract a bit mask(safe) by rowmask, # ldmask and rdmask. all set bits of 'safe'
# indicates the safe column index for queen
# placement of this iteration for row index(row).
safe = all_rows_filled & (~(rowmask |
ldmask | rdmask))
while (safe > 0 ):
# Extracts the right-most set bit
# (safe column index) where queen
# can be placed for this row
p = safe & ( - safe)
col = ( int )(math.log(p) / math.log( 2 ))
board[row][col] = 'Q'
# This is very important:
# we need to update rowmask, ldmask and rdmask
# for next row as safe index for queen placement
# will be decided by these three bit masks.
# We have all three rowmask, ldmask and
# rdmask as 0 in beginning. Suppose, we are placing
# queen at 1st column index at 0th row. rowmask, ldmask
# and rdmask will change for next row as below:
# rowmask's 1st bit will be set by OR operation
# rowmask = 00000000000000000000000000000010
# ldmask will change by setting 1st
# bit by OR operation and left shifting
# by 1 as it has to block the next column
# of next row because that will fall on left diagonal.
# ldmask = 00000000000000000000000000000100
# rdmask will change by setting 1st bit
# by OR operation and right shifting by 1
# as it has to block the previous column
# of next row because that will fall on right diagonal.
# rdmask = 00000000000000000000000000000001
# these bit masks will keep updated in each
# iteration for next row
solveBoard(board, row + 1 , rowmask|p, (ldmask|p) << 1 , (rdmask|p) >> 1 )
# Reset right-most set bit to 0 so, next
# iteration will continue by placing the queen
# at another safe column index of this row
safe = safe & (safe - 1 )
# Backtracking, replace 'Q' by ' '
board[row][col] = ' '
# Program to print board
def printBoard(board):
for row in board:
print ( "|" + "|" .join(row) + "|" )
# Driver Code
def main():
n = 4 ; # board size
board = []
for i in range (n):
row = []
for j in range (n):
row.append( ' ' )
board.append(row)
rowmask = 0
ldmask = 0
rdmask = 0
row = 0
# Function Call
solveBoard(board, row, rowmask, ldmask, rdmask)
# creates a new line
print ()
print ( "Number of ways to place " + ( str )(n) +
" queens : " + ( str )(ways))
if __name__ = = "__main__" :
main()
#This code is contributed by Nikhil Vinay输出如下
=====================
Queen placement - 1
=====================
| |Q| | |
| | | |Q|
|Q| | | |
| | |Q| |
=====================
Queen placement - 2
=====================
| | |Q| |
|Q| | | |
| | | |Q|
| |Q| | |
Number of ways to place 4 queens : 2如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)