建议参考以下帖子作为该帖子的前提条件。
B树|设置1(简介)
B树|套装2(插入)
B树是多路搜索树的一种。因此, 如果你通常对多向搜索树不熟悉, 那么最好看看IIT-Delhi的视频讲座, 然后再继续。一旦你清楚了多向搜索树的基础, B-Tree操作将更容易理解。
以下解释和算法的来源是算法入门第三版, 作者:Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
删除过程:
从B树中删除比插入要复杂得多, 因为我们可以从任何节点(不仅是叶子)中删除密钥, 而且从内部节点中删除密钥时, 我们必须重新排列该节点的子节点。
在插入过程中, 我们必须确保删除操作不违反B树属性。正如我们必须确保节点不会由于插入而变得太大一样, 我们也必须确保在删除过程中节点不会变得太小(除了允许根的根数小于最小t-1之外)键)。就像如果要插入密钥的路径上的节点已满, 可能需要备份简单的插入算法一样, 如果路径上的节点(不是根), 则必须备份一种简单的删除方法要删除密钥的位置的密钥数目最少。
删除过程从以x为根的子树中删除密钥k。该过程保证了, 无论何时它在节点x上递归调用, x中的键数至少为最小度t。请注意, 此条件所需的密钥比通常的B树条件所需的最小密钥多, 因此有时在递归下降到该子节点之前, 有时必须将一个密钥移入子节点。这种增强的条件使我们能够一次向下删除树中的密钥, 而不必"备份"(一个例外, 我们将对此进行解释)。你应该理解以下有关从B树中删除的规范, 并应理解, 如果根节点x成为没有密钥的内部节点(这种情况在情况2c和3b中可能会发生, 那么我们将删除x, 并且x是唯一的子x .c1成为树的新根, 将树的高度减一, 并保留该树的根包含至少一个键的属性(除非树为空)。
我们概述了删除如何与从B树中删除键的各种情况一起使用。
1.如果密钥k在节点x中并且x是叶, 请从x删除密钥k。
2.如果密钥k在节点x中并且x是内部节点, 请执行以下操作。
a)如果在节点x中在k之前的子y至少具有t个键, 则在以y为根的子树中找到k的前任k0。递归删除k0, 然后用x中的k0替换k。 (我们可以找到k0并在一次向下传递中将其删除。)
b)如果y的键数少于t, 则对称地检查节点x中紧随k的子级z。如果z至少具有t个键, 则在以z为根的子树中找到k的后继k0。递归删除k0, 然后用x中的k0替换k。 (我们可以找到k0并在一次向下传递中将其删除。)
c)否则, 如果y和z都只有t-1个键, 则将k和所有z合并到y中, 以便x失去k和指向z的指针, 并且y现在包含2t-1个键。然后释放z并从y中递归删除k。
3.如果内部节点x中不存在密钥k, 则如果k完全在树中, 则确定必须包含k的适当子树的根x.c(i)。如果x.c(i)只有t-1个键, 请根据需要执行步骤3a或3b, 以确保我们下降到包含至少t个键的节点。然后通过递归x的适当子元素来完成。
a)如果xc(i)仅具有t-1个键, 但具有至少t个键的直接同级, 则通过将键从x向下移动到xc(i), 再将键从xc(i )的直接向左或向右同级到x, 然后将适当的子指针从同级移动到xc(i)。
b)如果xc(i)和xc(i)的两个直接同级都具有t-1个密钥, 则将xc(i)与一个同级合并, 这涉及将密钥从x向下移动到新的合并节点中, 从而成为该节点。
由于B树中的大多数键都在叶子中, 因此删除操作最常用于从叶子中删除键。然后, 递归删除过程将向下执行一次, 无需进行备份。但是, 当删除内部节点中的密钥时, 该过程向下通过树, 但可能必须返回到删除密钥的节点, 才能用其前任或后继替换密钥(情况2a和2b)。
下图说明了删除过程。
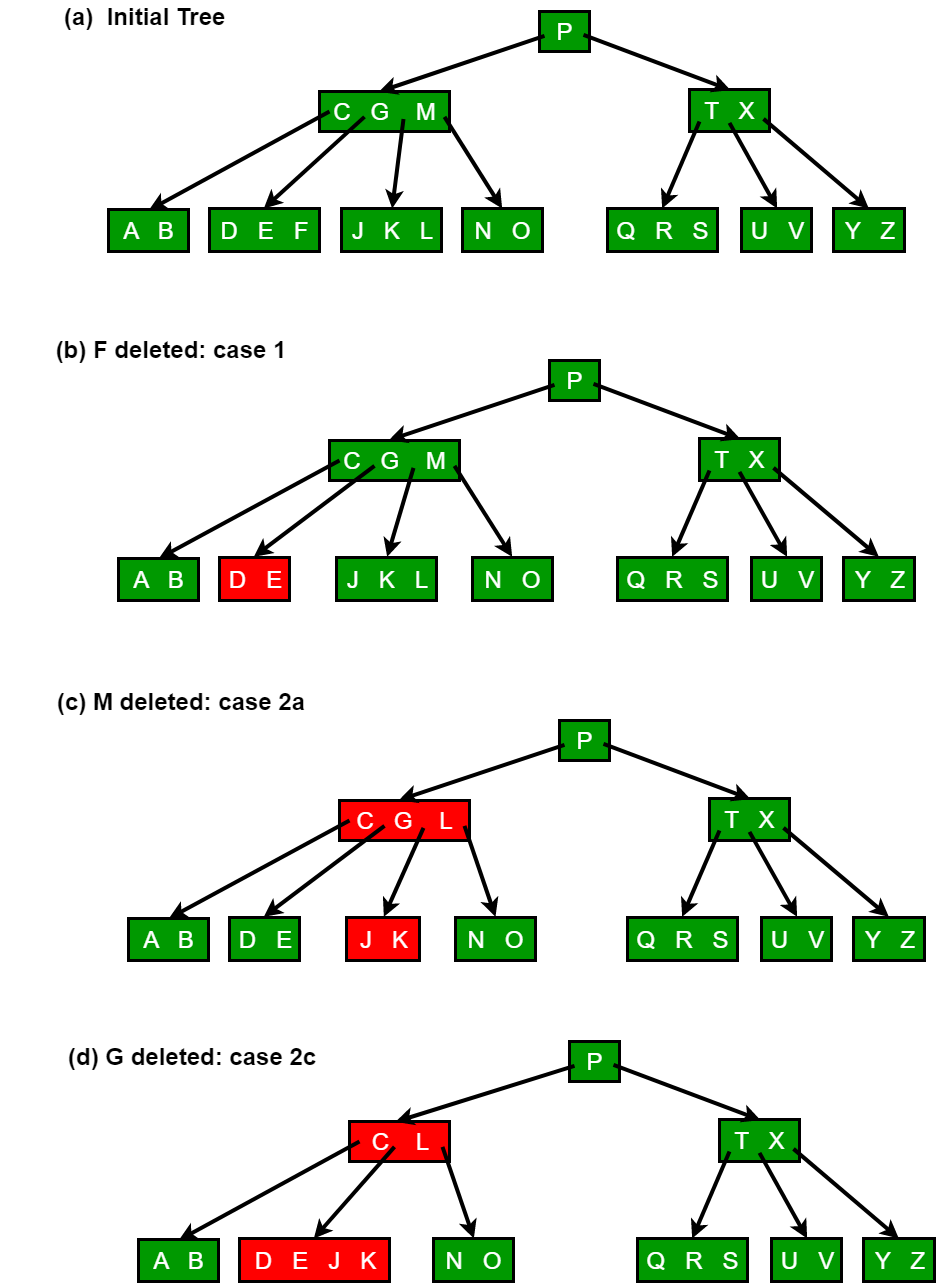
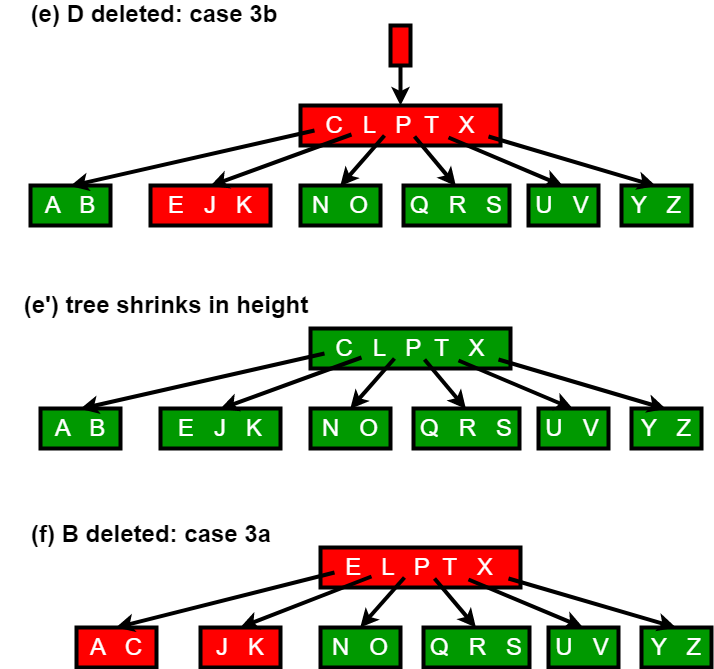
实现
以下是删除过程的C ++实现。
/* The following program performs deletion on a B-Tree. It contains functions
specific for deletion along with all the other functions provided in the
previous articles on B-Trees. See https://www.lsbin.org/b-tree-set-1-introduction-2/
for previous article.
The deletion function has been compartmentalized into 8 functions for ease
of understanding and clarity
The following functions are exclusive for deletion
In class BTreeNode:
1) remove
2) removeFromLeaf
3) removeFromNonLeaf
4) getPred
5) getSucc
6) borrowFromPrev
7) borrowFromNext
8) merge
9) findKey
In class BTree:
1) remove
The removal of a key from a B-Tree is a fairly complicated process. The program handles
all the 6 different cases that might arise while removing a key.
Testing: The code has been tested using the B-Tree provided in the CLRS book( included
in the main function ) along with other cases.
Reference: CLRS3 - Chapter 18 - (499-502)
It is advised to read the material in CLRS before taking a look at the code. */
#include<iostream>
using namespace std;
// A BTree node
class BTreeNode
{
int *keys; // An array of keys
int t; // Minimum degree (defines the range for number of keys)
BTreeNode **C; // An array of child pointers
int n; // Current number of keys
bool leaf; // Is true when node is leaf. Otherwise false
public :
BTreeNode( int _t, bool _leaf); // Constructor
// A function to traverse all nodes in a subtree rooted with this node
void traverse();
// A function to search a key in subtree rooted with this node.
BTreeNode *search( int k); // returns NULL if k is not present.
// A function that returns the index of the first key that is greater
// or equal to k
int findKey( int k);
// A utility function to insert a new key in the subtree rooted with
// this node. The assumption is, the node must be non-full when this
// function is called
void insertNonFull( int k);
// A utility function to split the child y of this node. i is index
// of y in child array C[]. The Child y must be full when this
// function is called
void splitChild( int i, BTreeNode *y);
// A wrapper function to remove the key k in subtree rooted with
// this node.
void remove ( int k);
// A function to remove the key present in idx-th position in
// this node which is a leaf
void removeFromLeaf( int idx);
// A function to remove the key present in idx-th position in
// this node which is a non-leaf node
void removeFromNonLeaf( int idx);
// A function to get the predecessor of the key- where the key
// is present in the idx-th position in the node
int getPred( int idx);
// A function to get the successor of the key- where the key
// is present in the idx-th position in the node
int getSucc( int idx);
// A function to fill up the child node present in the idx-th
// position in the C[] array if that child has less than t-1 keys
void fill( int idx);
// A function to borrow a key from the C[idx-1]-th node and place
// it in C[idx]th node
void borrowFromPrev( int idx);
// A function to borrow a key from the C[idx+1]-th node and place it
// in C[idx]th node
void borrowFromNext( int idx);
// A function to merge idx-th child of the node with (idx+1)th child of
// the node
void merge( int idx);
// Make BTree friend of this so that we can access private members of
// this class in BTree functions
friend class BTree;
};
class BTree
{
BTreeNode *root; // Pointer to root node
int t; // Minimum degree
public :
// Constructor (Initializes tree as empty)
BTree( int _t)
{
root = NULL;
t = _t;
}
void traverse()
{
if (root != NULL) root->traverse();
}
// function to search a key in this tree
BTreeNode* search( int k)
{
return (root == NULL)? NULL : root->search(k);
}
// The main function that inserts a new key in this B-Tree
void insert( int k);
// The main function that removes a new key in thie B-Tree
void remove ( int k);
};
BTreeNode::BTreeNode( int t1, bool leaf1)
{
// Copy the given minimum degree and leaf property
t = t1;
leaf = leaf1;
// Allocate memory for maximum number of possible keys
// and child pointers
keys = new int [2*t-1];
C = new BTreeNode *[2*t];
// Initialize the number of keys as 0
n = 0;
}
// A utility function that returns the index of the first key that is
// greater than or equal to k
int BTreeNode::findKey( int k)
{
int idx=0;
while (idx<n && keys[idx] < k)
++idx;
return idx;
}
// A function to remove the key k from the sub-tree rooted with this node
void BTreeNode:: remove ( int k)
{
int idx = findKey(k);
// The key to be removed is present in this node
if (idx < n && keys[idx] == k)
{
// If the node is a leaf node - removeFromLeaf is called
// Otherwise, removeFromNonLeaf function is called
if (leaf)
removeFromLeaf(idx);
else
removeFromNonLeaf(idx);
}
else
{
// If this node is a leaf node, then the key is not present in tree
if (leaf)
{
cout << "The key " << k << " is does not exist in the tree\n" ;
return ;
}
// The key to be removed is present in the sub-tree rooted with this node
// The flag indicates whether the key is present in the sub-tree rooted
// with the last child of this node
bool flag = ( (idx==n)? true : false );
// If the child where the key is supposed to exist has less that t keys, // we fill that child
if (C[idx]->n < t)
fill(idx);
// If the last child has been merged, it must have merged with the previous
// child and so we recurse on the (idx-1)th child. Else, we recurse on the
// (idx)th child which now has atleast t keys
if (flag && idx > n)
C[idx-1]-> remove (k);
else
C[idx]-> remove (k);
}
return ;
}
// A function to remove the idx-th key from this node - which is a leaf node
void BTreeNode::removeFromLeaf ( int idx)
{
// Move all the keys after the idx-th pos one place backward
for ( int i=idx+1; i<n; ++i)
keys[i-1] = keys[i];
// Reduce the count of keys
n--;
return ;
}
// A function to remove the idx-th key from this node - which is a non-leaf node
void BTreeNode::removeFromNonLeaf( int idx)
{
int k = keys[idx];
// If the child that precedes k (C[idx]) has atleast t keys, // find the predecessor 'pred' of k in the subtree rooted at
// C[idx]. Replace k by pred. Recursively delete pred
// in C[idx]
if (C[idx]->n >= t)
{
int pred = getPred(idx);
keys[idx] = pred;
C[idx]-> remove (pred);
}
// If the child C[idx] has less that t keys, examine C[idx+1].
// If C[idx+1] has atleast t keys, find the successor 'succ' of k in
// the subtree rooted at C[idx+1]
// Replace k by succ
// Recursively delete succ in C[idx+1]
else if (C[idx+1]->n >= t)
{
int succ = getSucc(idx);
keys[idx] = succ;
C[idx+1]-> remove (succ);
}
// If both C[idx] and C[idx+1] has less that t keys, merge k and all of C[idx+1]
// into C[idx]
// Now C[idx] contains 2t-1 keys
// Free C[idx+1] and recursively delete k from C[idx]
else
{
merge(idx);
C[idx]-> remove (k);
}
return ;
}
// A function to get predecessor of keys[idx]
int BTreeNode::getPred( int idx)
{
// Keep moving to the right most node until we reach a leaf
BTreeNode *cur=C[idx];
while (!cur->leaf)
cur = cur->C[cur->n];
// Return the last key of the leaf
return cur->keys[cur->n-1];
}
int BTreeNode::getSucc( int idx)
{
// Keep moving the left most node starting from C[idx+1] until we reach a leaf
BTreeNode *cur = C[idx+1];
while (!cur->leaf)
cur = cur->C[0];
// Return the first key of the leaf
return cur->keys[0];
}
// A function to fill child C[idx] which has less than t-1 keys
void BTreeNode::fill( int idx)
{
// If the previous child(C[idx-1]) has more than t-1 keys, borrow a key
// from that child
if (idx!=0 && C[idx-1]->n>=t)
borrowFromPrev(idx);
// If the next child(C[idx+1]) has more than t-1 keys, borrow a key
// from that child
else if (idx!=n && C[idx+1]->n>=t)
borrowFromNext(idx);
// Merge C[idx] with its sibling
// If C[idx] is the last child, merge it with with its previous sibling
// Otherwise merge it with its next sibling
else
{
if (idx != n)
merge(idx);
else
merge(idx-1);
}
return ;
}
// A function to borrow a key from C[idx-1] and insert it
// into C[idx]
void BTreeNode::borrowFromPrev( int idx)
{
BTreeNode *child=C[idx];
BTreeNode *sibling=C[idx-1];
// The last key from C[idx-1] goes up to the parent and key[idx-1]
// from parent is inserted as the first key in C[idx]. Thus, the loses
// sibling one key and child gains one key
// Moving all key in C[idx] one step ahead
for ( int i=child->n-1; i>=0; --i)
child->keys[i+1] = child->keys[i];
// If C[idx] is not a leaf, move all its child pointers one step ahead
if (!child->leaf)
{
for ( int i=child->n; i>=0; --i)
child->C[i+1] = child->C[i];
}
// Setting child's first key equal to keys[idx-1] from the current node
child->keys[0] = keys[idx-1];
// Moving sibling's last child as C[idx]'s first child
if (!child->leaf)
child->C[0] = sibling->C[sibling->n];
// Moving the key from the sibling to the parent
// This reduces the number of keys in the sibling
keys[idx-1] = sibling->keys[sibling->n-1];
child->n += 1;
sibling->n -= 1;
return ;
}
// A function to borrow a key from the C[idx+1] and place
// it in C[idx]
void BTreeNode::borrowFromNext( int idx)
{
BTreeNode *child=C[idx];
BTreeNode *sibling=C[idx+1];
// keys[idx] is inserted as the last key in C[idx]
child->keys[(child->n)] = keys[idx];
// Sibling's first child is inserted as the last child
// into C[idx]
if (!(child->leaf))
child->C[(child->n)+1] = sibling->C[0];
//The first key from sibling is inserted into keys[idx]
keys[idx] = sibling->keys[0];
// Moving all keys in sibling one step behind
for ( int i=1; i<sibling->n; ++i)
sibling->keys[i-1] = sibling->keys[i];
// Moving the child pointers one step behind
if (!sibling->leaf)
{
for ( int i=1; i<=sibling->n; ++i)
sibling->C[i-1] = sibling->C[i];
}
// Increasing and decreasing the key count of C[idx] and C[idx+1]
// respectively
child->n += 1;
sibling->n -= 1;
return ;
}
// A function to merge C[idx] with C[idx+1]
// C[idx+1] is freed after merging
void BTreeNode::merge( int idx)
{
BTreeNode *child = C[idx];
BTreeNode *sibling = C[idx+1];
// Pulling a key from the current node and inserting it into (t-1)th
// position of C[idx]
child->keys[t-1] = keys[idx];
// Copying the keys from C[idx+1] to C[idx] at the end
for ( int i=0; i<sibling->n; ++i)
child->keys[i+t] = sibling->keys[i];
// Copying the child pointers from C[idx+1] to C[idx]
if (!child->leaf)
{
for ( int i=0; i<=sibling->n; ++i)
child->C[i+t] = sibling->C[i];
}
// Moving all keys after idx in the current node one step before -
// to fill the gap created by moving keys[idx] to C[idx]
for ( int i=idx+1; i<n; ++i)
keys[i-1] = keys[i];
// Moving the child pointers after (idx+1) in the current node one
// step before
for ( int i=idx+2; i<=n; ++i)
C[i-1] = C[i];
// Updating the key count of child and the current node
child->n += sibling->n+1;
n--;
// Freeing the memory occupied by sibling
delete (sibling);
return ;
}
// The main function that inserts a new key in this B-Tree
void BTree::insert( int k)
{
// If tree is empty
if (root == NULL)
{
// Allocate memory for root
root = new BTreeNode(t, true );
root->keys[0] = k; // Insert key
root->n = 1; // Update number of keys in root
}
else // If tree is not empty
{
// If root is full, then tree grows in height
if (root->n == 2*t-1)
{
// Allocate memory for new root
BTreeNode *s = new BTreeNode(t, false );
// Make old root as child of new root
s->C[0] = root;
// Split the old root and move 1 key to the new root
s->splitChild(0, root);
// New root has two children now. Decide which of the
// two children is going to have new key
int i = 0;
if (s->keys[0] < k)
i++;
s->C[i]->insertNonFull(k);
// Change root
root = s;
}
else // If root is not full, call insertNonFull for root
root->insertNonFull(k);
}
}
// A utility function to insert a new key in this node
// The assumption is, the node must be non-full when this
// function is called
void BTreeNode::insertNonFull( int k)
{
// Initialize index as index of rightmost element
int i = n-1;
// If this is a leaf node
if (leaf == true )
{
// The following loop does two things
// a) Finds the location of new key to be inserted
// b) Moves all greater keys to one place ahead
while (i >= 0 && keys[i] > k)
{
keys[i+1] = keys[i];
i--;
}
// Insert the new key at found location
keys[i+1] = k;
n = n+1;
}
else // If this node is not leaf
{
// Find the child which is going to have the new key
while (i >= 0 && keys[i] > k)
i--;
// See if the found child is full
if (C[i+1]->n == 2*t-1)
{
// If the child is full, then split it
splitChild(i+1, C[i+1]);
// After split, the middle key of C[i] goes up and
// C[i] is splitted into two. See which of the two
// is going to have the new key
if (keys[i+1] < k)
i++;
}
C[i+1]->insertNonFull(k);
}
}
// A utility function to split the child y of this node
// Note that y must be full when this function is called
void BTreeNode::splitChild( int i, BTreeNode *y)
{
// Create a new node which is going to store (t-1) keys
// of y
BTreeNode *z = new BTreeNode(y->t, y->leaf);
z->n = t - 1;
// Copy the last (t-1) keys of y to z
for ( int j = 0; j < t-1; j++)
z->keys[j] = y->keys[j+t];
// Copy the last t children of y to z
if (y->leaf == false )
{
for ( int j = 0; j < t; j++)
z->C[j] = y->C[j+t];
}
// Reduce the number of keys in y
y->n = t - 1;
// Since this node is going to have a new child, // create space of new child
for ( int j = n; j >= i+1; j--)
C[j+1] = C[j];
// Link the new child to this node
C[i+1] = z;
// A key of y will move to this node. Find location of
// new key and move all greater keys one space ahead
for ( int j = n-1; j >= i; j--)
keys[j+1] = keys[j];
// Copy the middle key of y to this node
keys[i] = y->keys[t-1];
// Increment count of keys in this node
n = n + 1;
}
// Function to traverse all nodes in a subtree rooted with this node
void BTreeNode::traverse()
{
// There are n keys and n+1 children, travers through n keys
// and first n children
int i;
for (i = 0; i < n; i++)
{
// If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i].
if (leaf == false )
C[i]->traverse();
cout << " " << keys[i];
}
// Print the subtree rooted with last child
if (leaf == false )
C[i]->traverse();
}
// Function to search key k in subtree rooted with this node
BTreeNode *BTreeNode::search( int k)
{
// Find the first key greater than or equal to k
int i = 0;
while (i < n && k > keys[i])
i++;
// If the found key is equal to k, return this node
if (keys[i] == k)
return this ;
// If key is not found here and this is a leaf node
if (leaf == true )
return NULL;
// Go to the appropriate child
return C[i]->search(k);
}
void BTree:: remove ( int k)
{
if (!root)
{
cout << "The tree is empty\n" ;
return ;
}
// Call the remove function for root
root-> remove (k);
// If the root node has 0 keys, make its first child as the new root
// if it has a child, otherwise set root as NULL
if (root->n==0)
{
BTreeNode *tmp = root;
if (root->leaf)
root = NULL;
else
root = root->C[0];
// Free the old root
delete tmp;
}
return ;
}
// Driver program to test above functions
int main()
{
BTree t(3); // A B-Tree with minium degree 3
t.insert(1);
t.insert(3);
t.insert(7);
t.insert(10);
t.insert(11);
t.insert(13);
t.insert(14);
t.insert(15);
t.insert(18);
t.insert(16);
t.insert(19);
t.insert(24);
t.insert(25);
t.insert(26);
t.insert(21);
t.insert(4);
t.insert(5);
t.insert(20);
t.insert(22);
t.insert(2);
t.insert(17);
t.insert(12);
t.insert(6);
cout << "Traversal of tree constructed is\n" ;
t.traverse();
cout << endl;
t. remove (6);
cout << "Traversal of tree after removing 6\n" ;
t.traverse();
cout << endl;
t. remove (13);
cout << "Traversal of tree after removing 13\n" ;
t.traverse();
cout << endl;
t. remove (7);
cout << "Traversal of tree after removing 7\n" ;
t.traverse();
cout << endl;
t. remove (4);
cout << "Traversal of tree after removing 4\n" ;
t.traverse();
cout << endl;
t. remove (2);
cout << "Traversal of tree after removing 2\n" ;
t.traverse();
cout << endl;
t. remove (16);
cout << "Traversal of tree after removing 16\n" ;
t.traverse();
cout << endl;
return 0;
}输出如下:
Traversal of tree constructed is
1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 19 20 21 22 24 25 26
Traversal of tree after removing 6
1 2 3 4 5 7 10 11 12 13 14 15 16 17 18 19 20 21 22 24 25 26
Traversal of tree after removing 13
1 2 3 4 5 7 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26
Traversal of tree after removing 7
1 2 3 4 5 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26
Traversal of tree after removing 4
1 2 3 5 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26
Traversal of tree after removing 2
1 3 5 10 11 12 14 15 16 17 18 19 20 21 22 24 25 26
Traversal of tree after removing 16
1 3 5 10 11 12 14 15 17 18 19 20 21 22 24 25 26本文作者:Balasubramanian。如果发现任何不正确的地方, 或者想分享有关上述主题的更多信息, 请写评论。

![从字法上最小长度N的排列,使得对于正好为K个索引,a[i] a[i]+1](https://www.lsbin.com/wp-content/themes/begin%20lts/img/loading.png)